移項とは?
移項とは
=を越えて移動させると性質が逆になる計算方法
性質が逆のもの
| +⇔- | ×⇔÷ |
例題
| 解き方 | 説明 |
| \(2x\)\(-3\)=\(7\) | |
| \(2x\)=\(7\)\(+3\) | -3が=を越えて移動したので 符号が逆(-が+)になりました |
| \(2x\)=\(10\) | \(2x\)は、\(2\times x\) かけ算の意味なので |
| \(x\)=\(10\div 2\) | \(2\)が=を越えて移動すると 割り算になります |
| \(x=5\) |
簡単に言うと、これが移項の計算方法です。
でもなぜそうなるのか?疑問に思う方は以下をご覧下さい。
なぜ=を越えて移動すると性質が逆になるのか
等式の性質
移項は元々「等式の性質」からきています。
等式の性質とは
「=」をはさんだ両側に同じ計算を付け加えると
数字はかわるが「=」であることは変わらないという性質
等式は「てんびん」と同じです。
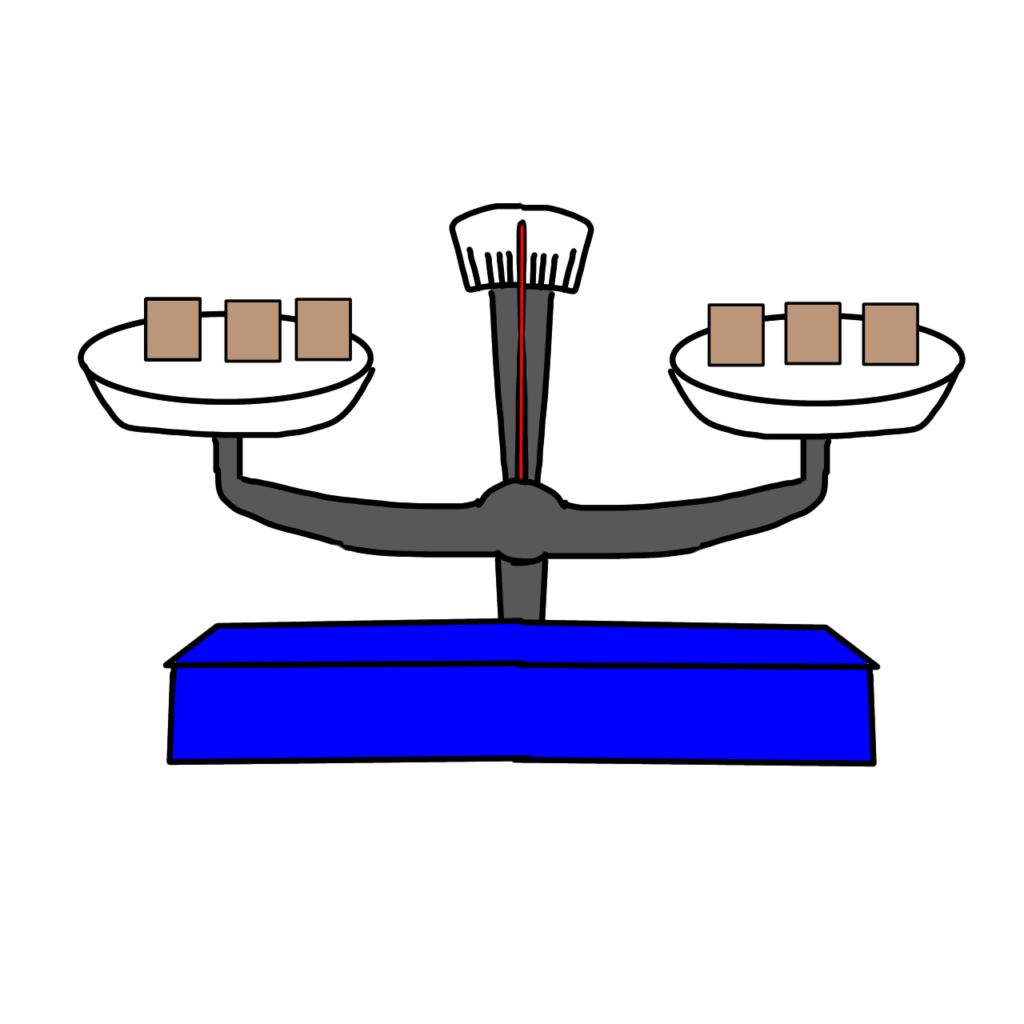
左右両方に同じものが3こずつなのでつり合っています
3=3
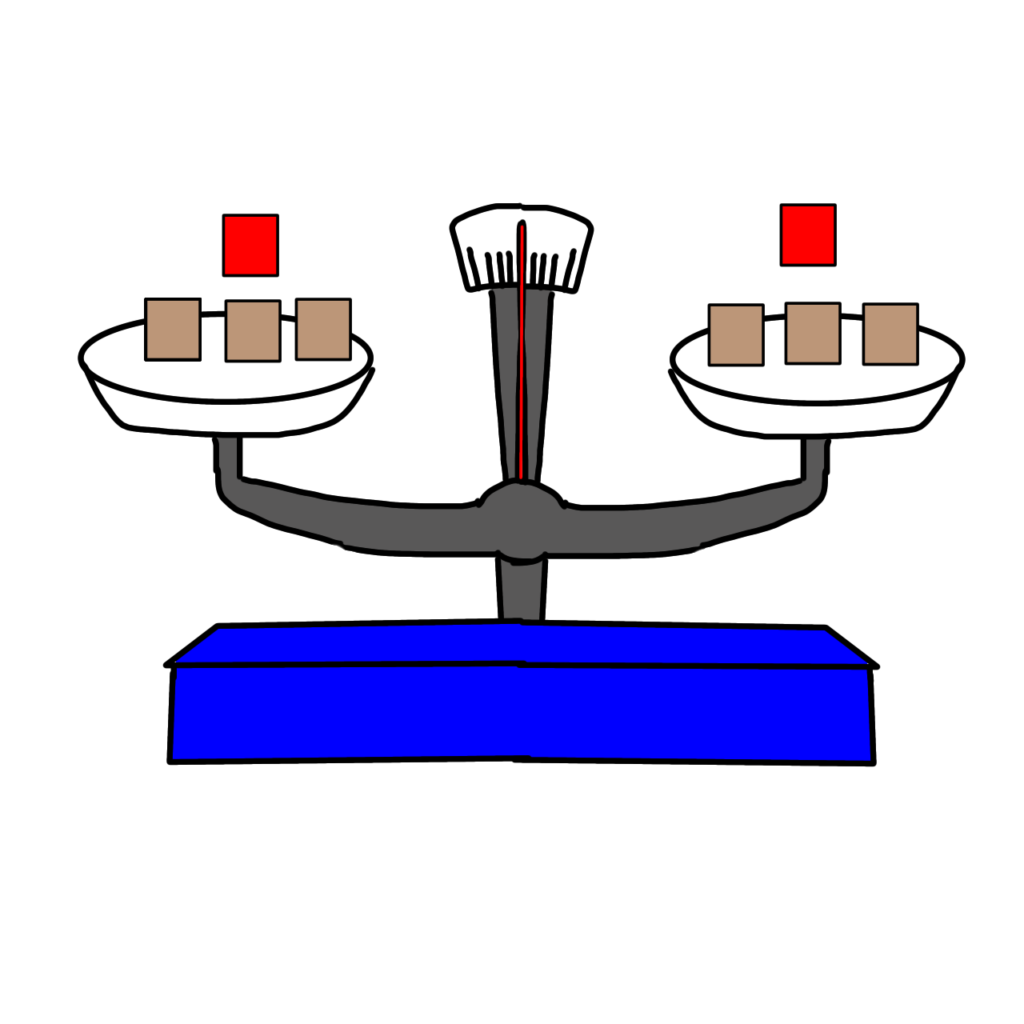
そこに、同じものを1個ずつ足しても、つり合います。
3+1=3+1
4=4
数字は変わりますが、=であることは変わりません
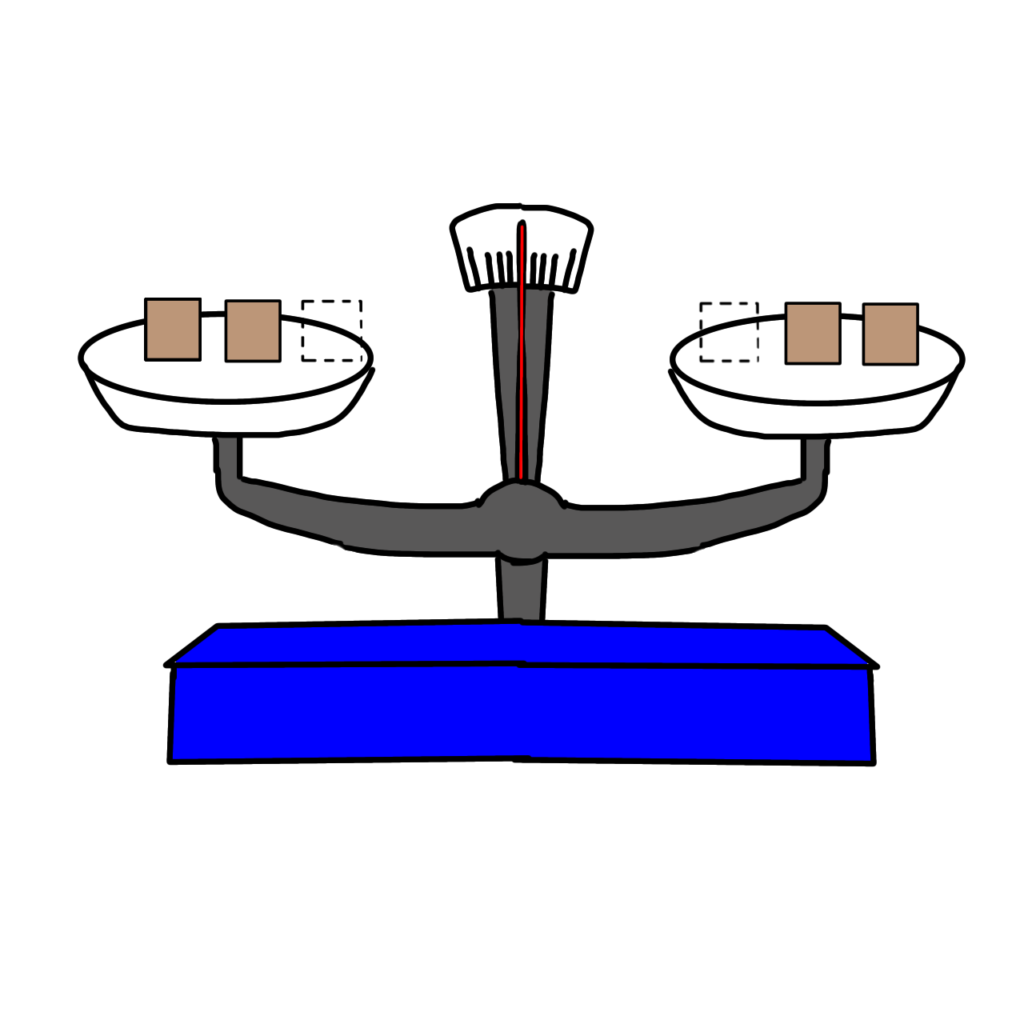
同じものを1個ずつ引いても、つり合います。
3-1=3-1
2=2
この場合も数字は変わりますが、
=であることは変わりません
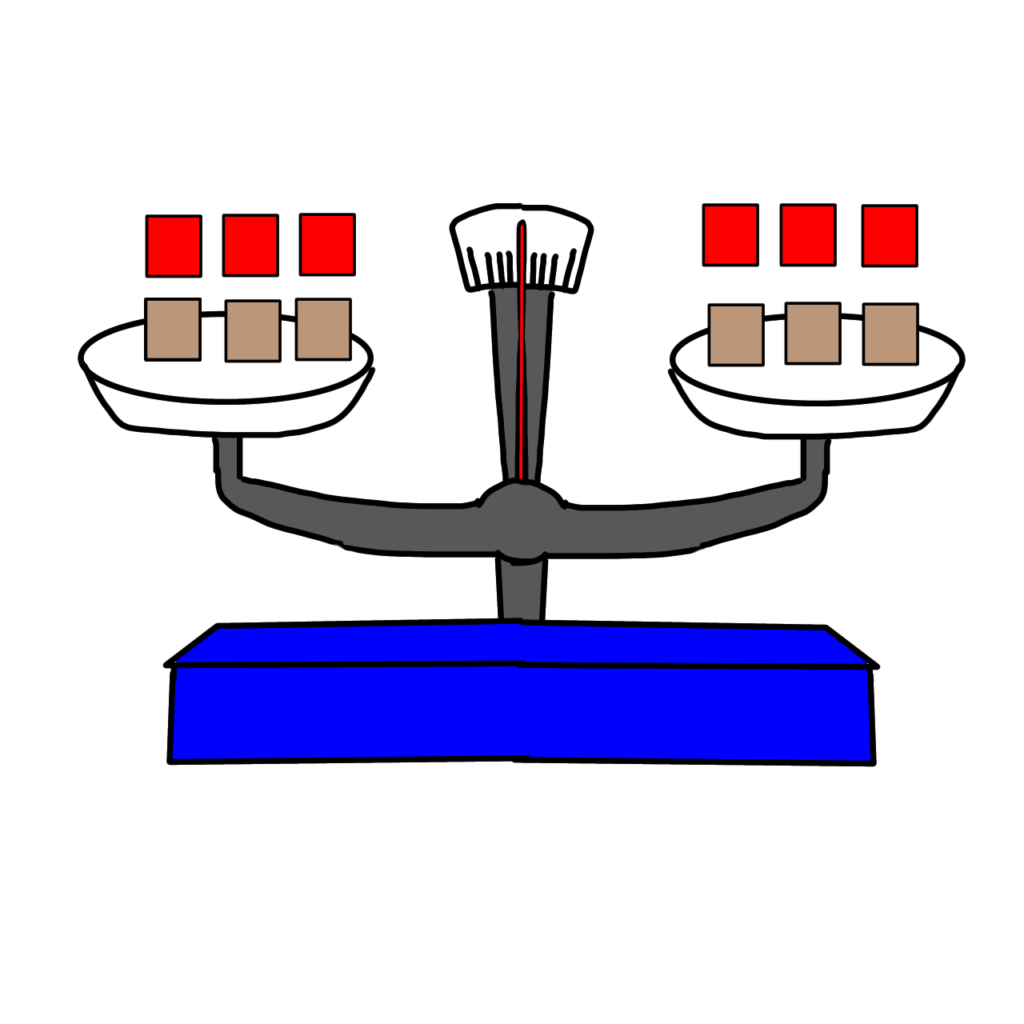
両方とも2倍にしてもつり合います。
3×2=3×2
6=6
やっぱり=であることは変わりません
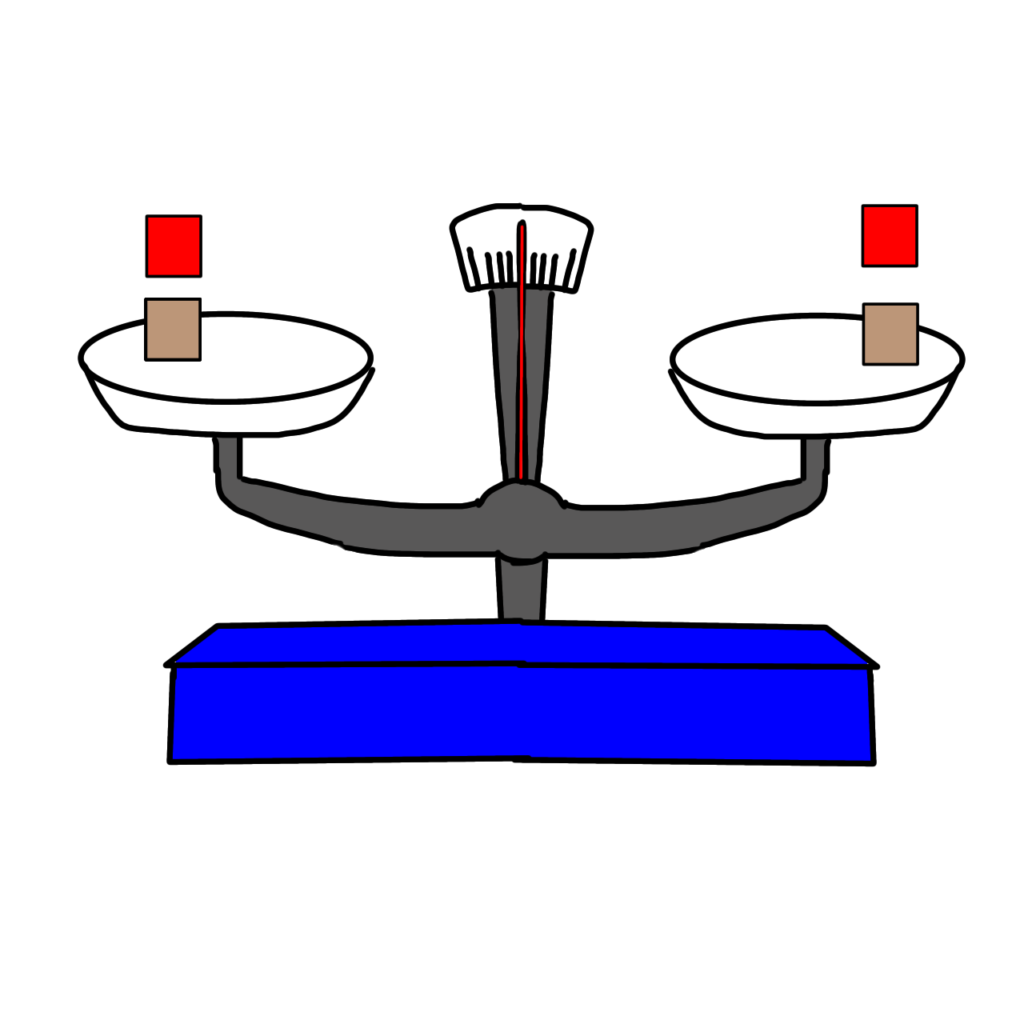
6個になった両方を、3で割ってもつり合います。
6÷3=6÷3
2=2
これでも=であることは変わりません
このように、=の右側と左側に同じ処理をすれば数字は変わるけれど、「=」であることは変わらないのです。
これを使って方程式を解いてみましょう。
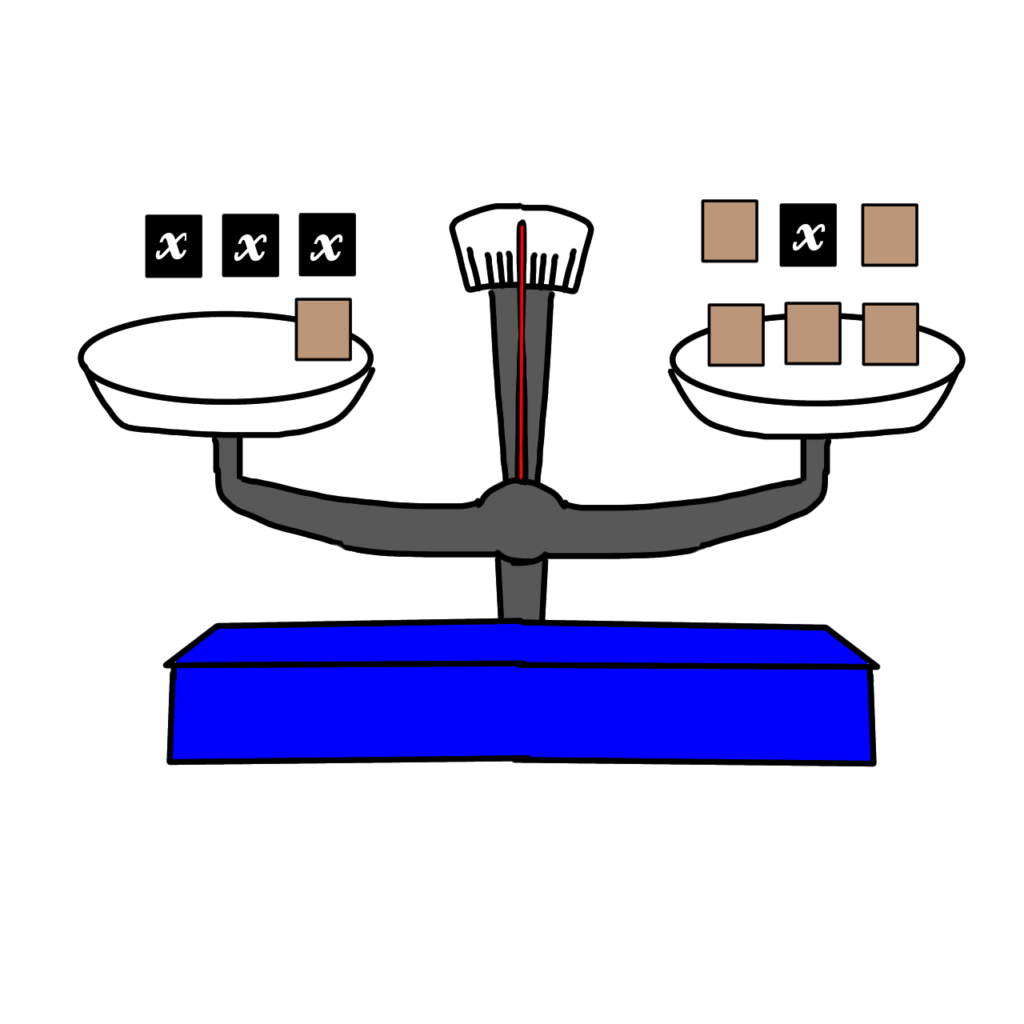
重さの分からないものが\(x\)だとします。
左には\(x\)が3個と普通のおもり1個
右には\(x\)が1個と普通のおもり5個あってつり合っています。つまり、
\(3x+1=x+5\)
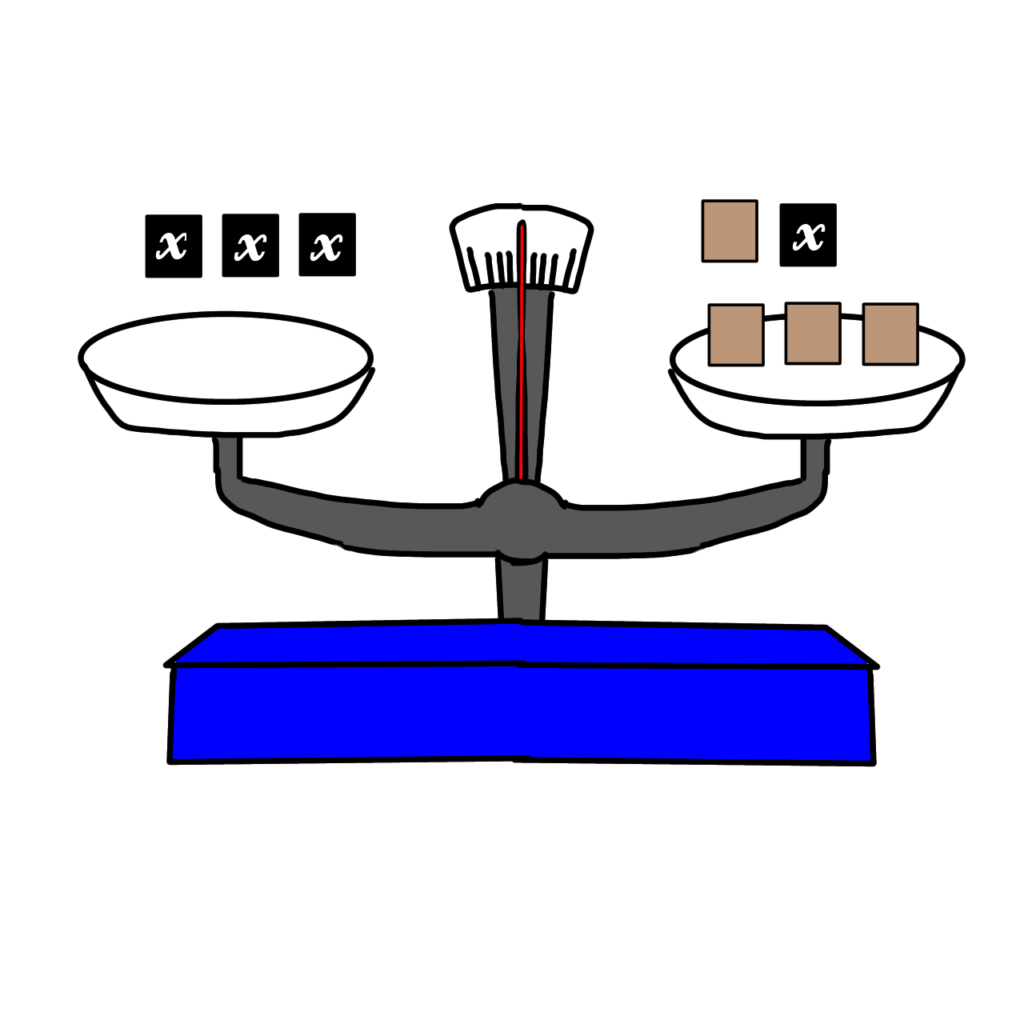
普通のおもり1個ずつをはずすと
\(3x+1\)\(-1\)\(=x+5\)\(-1\)
左側だけ計算すると
\(3x=x+5\)\(-1\)
右側も計算すると
\(3x=x+4\)
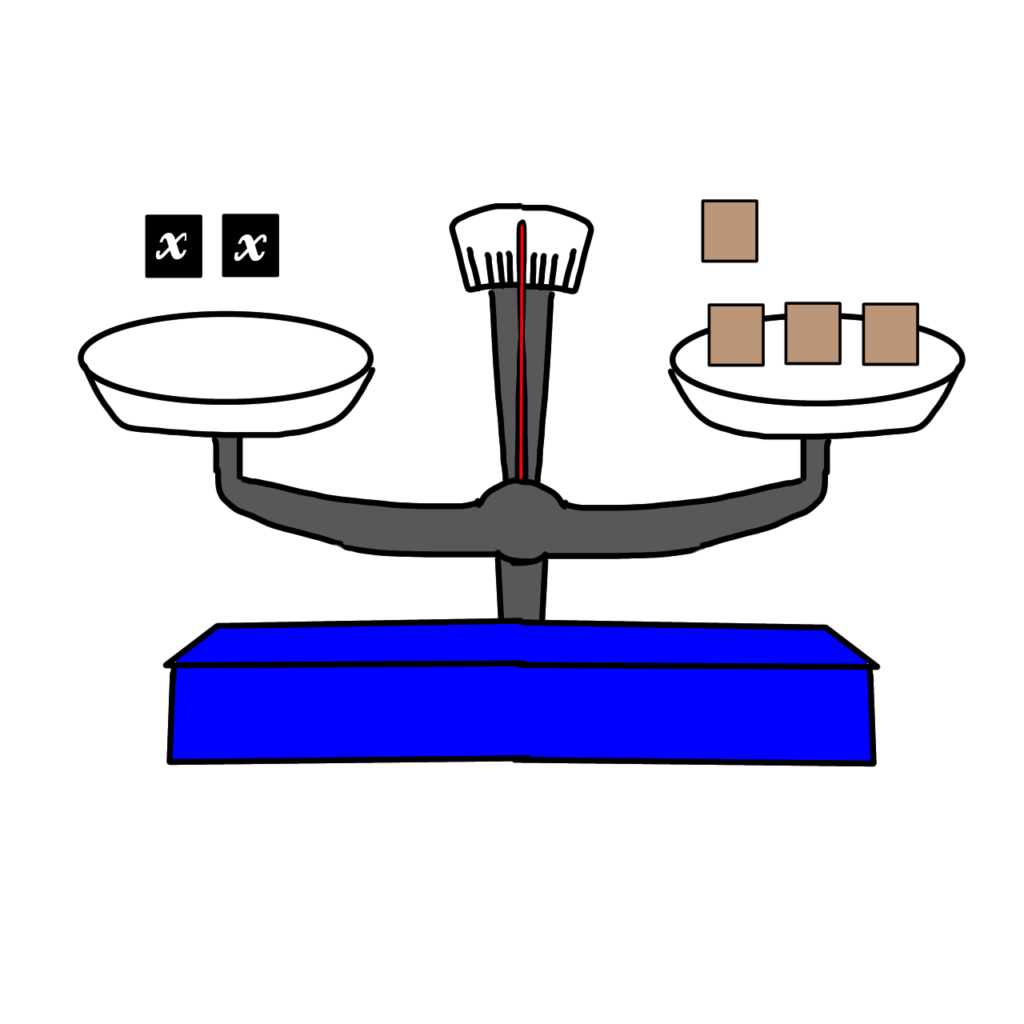
次に\(x\)を1個ずつはずしていきます。
\(3x\)\(-x\)\(=x+4\)\(-x\)
右側だけ計算すると
\(3x\)\(-x\)\(=4\)
左側も計算すると
\(2x=4\)
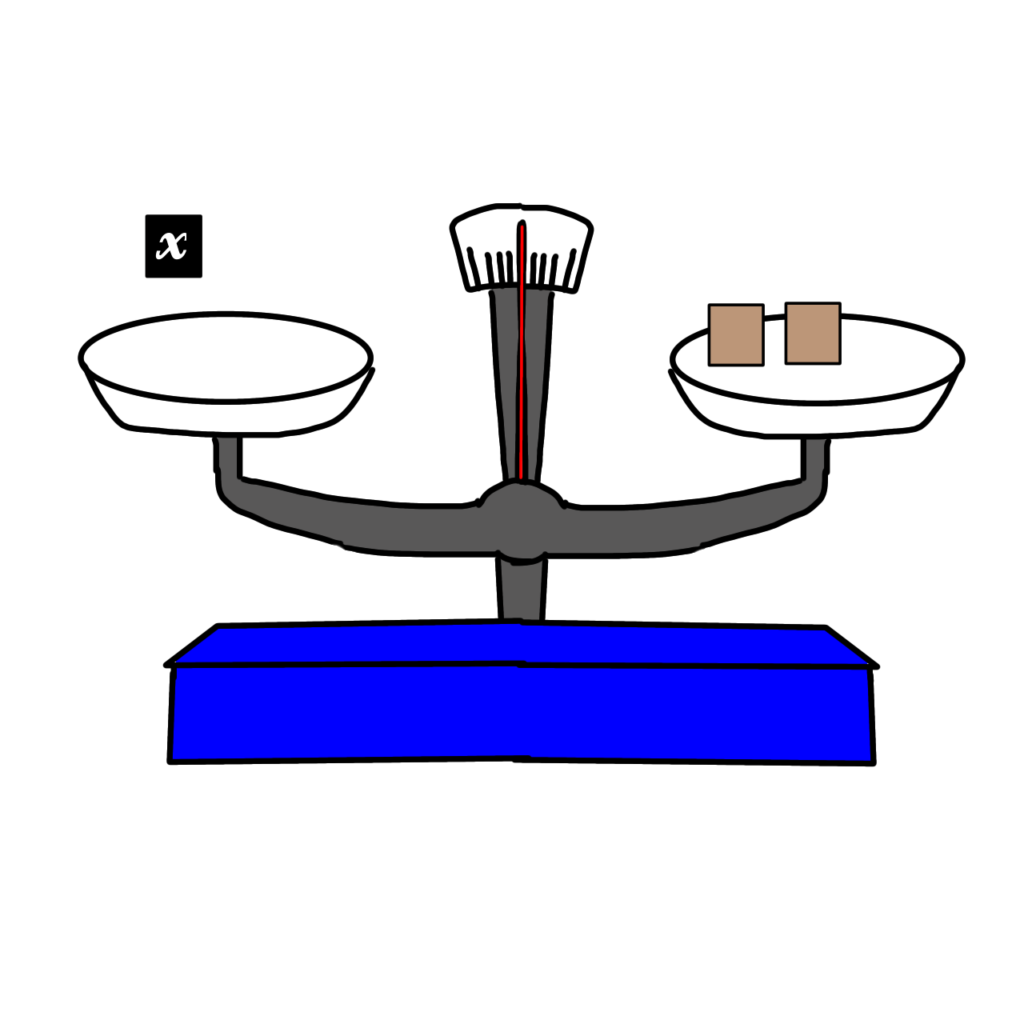
両方を2で割れば\(x\)の重さがわかります。
\(\dfrac{2x}{2}=\dfrac{4}{2}\)
\(x=2\)
こんな感じで解けますが、この計算式だけをピックアップして移項を考えます。
※上の例では割り算を分数で計算しました。\(x\) についている整数を両辺の分母にすれば自動的に答えが出てきます。こう考えると、答えが分数になるときでもスムーズに答えが出せるのでオススメです。
例
\(3x=7\)
\(\dfrac{3x}{3}=\dfrac{7}{3}\)
\(x=\dfrac{7}{3}\)
移項とは?
移項と等式の性質の関係
先程、等式の性質を利用して細かく計算したものが左。移項の考え方が右です。
| 等式の性質を利用 | 移項の考え方 |
| \(3x+1=x+5\) | \(3x+1=x+5\) |
| \(3x+1\)\(-1\)\(=x+5\)\(-1\) | 左側の\(+1\)\(-1\)は 結局0になるので、 この途中計算を飛ばします |
| \(3x=x+5\)\(-1\) | \(3x=x+5\)\(-1\) |
| \(3x=x+4\) | \(3x=x+4\) |
| \(3x\)\(-x\)\(=x+4\)\(-x\) | 右側の\(x\)\(-x\)は 結局0になるので、 この途中計算を飛ばします |
| \(3x\)\(-x\)\(=4\) | \(3x\)\(-x\)\(=4\) |
| \(2x=4\) | \(2x=4\) |
| \(\dfrac{2x}{2}=\dfrac{4}{2}\) | \(\dfrac{2x}{2}=\dfrac{4}{2}\) |
| \(x=2\) | \(x=2\) |
移項の考え方
途中計算を飛ばすところを除いて、移項の考え方の方だけまとめます。
| 移項の考え方 | 説明 |
| \(3x+1=x+5\) | |
| \(3x=x+5\)\(-1\) | 1行飛ばしたことで 左の+1が右に行って -1に変わったように 見えます |
| \(3x=x+4\) | |
| \(3x\)\(-x\)\(=4\) | 1行飛ばしたことで 右の\(x\)が左に行って \(-x\)に変わったように 見えます |
| \(2x=4\) | |
| \(\dfrac{2x}{2}=\dfrac{4}{2}\) | \(x\)に付いている 数で両辺を割ります |
| \(x=2\) | そうすると答えが わかります |
このような考えで、移項というものは行われています。
移項は「等式の性質」を省略したものなのです。
結果的に=を越えて移動した数は符号が逆転することになるわけですね。
理屈さえ分かれば、もっと計算式を簡単にできます。
移項を使った計算(実用的な方法)
| 移項の考え方 | 説明 |
| \(3x+1=x+5\) | \(x\)の付いた数を左 数字を右に集めます |
| \(3x\)\(-x\)\(=\)\(+5\)\(-1\) | =を越えて移動したら 符号が逆になります |
| \(2x=4\) | \(x\)は\(x\)同士 数字は数字同士 まとめます |
| \(\dfrac{2x}{2}=\dfrac{4}{2}\) | \(x\)に付いている 数で両辺を割ります |
| \(x=2\) | そうすると答えが わかります |
まとめ
なぜ=を越えて移動すると符号が逆になるのか?
それは、本当は「等式の性質」の考えを使って解いているのに、0になってなくなる途中計算を飛ばしたから急に符号が逆になったように見えるだけなのです。
ただ、簡単に求めるようにした結果「=を越えて移動すると符号が逆になる」計算方法になっただけなのです。
通常、この「移項」の考え方で方程式は解きます。「=」が付いた式ではこの考え方を使いますので、数学を解く上で必須の考え方です。
是非、使い慣れておきましょう。
補足:符号が変わらない「移動」
=を越えない移動は「移項」ではないので、符号は逆になりません。
| 解き方 | 説明 |
| \(-4x\)\(-5\)\(+2x\)\(=7\)\(+x\) | \(x\)の付いた数を左 数字を右に集めます |
| \(-4x\)\(+2x\)\(-x\)\(=7\)\(+5\) | =を越えた移動なので 符号は逆になります |
| \(2x\)\(-4x\)\(-x\)\(=7\)\(+5\) | 同じ符号同士を集めるため \(2x\)と\(-4x\)を入れ替えましたが =を越えない移動なので 符号は変わりません |
| \(2x-5x=12\) | |
| \(-3x=12\) | |
| \(\dfrac{-3x}{-3}=\dfrac{12}{-3}\) | \(x\)についている-3で 両辺を割ります |
| \(x=-4\) | そうすると答えが わかります |
=を越えない限り「移項」ではありませんので、その場合は符号を逆にしないように注意しましょう。
注意点
=を越えない移動は「移項」ではない!
符号はそのままで!


コメント