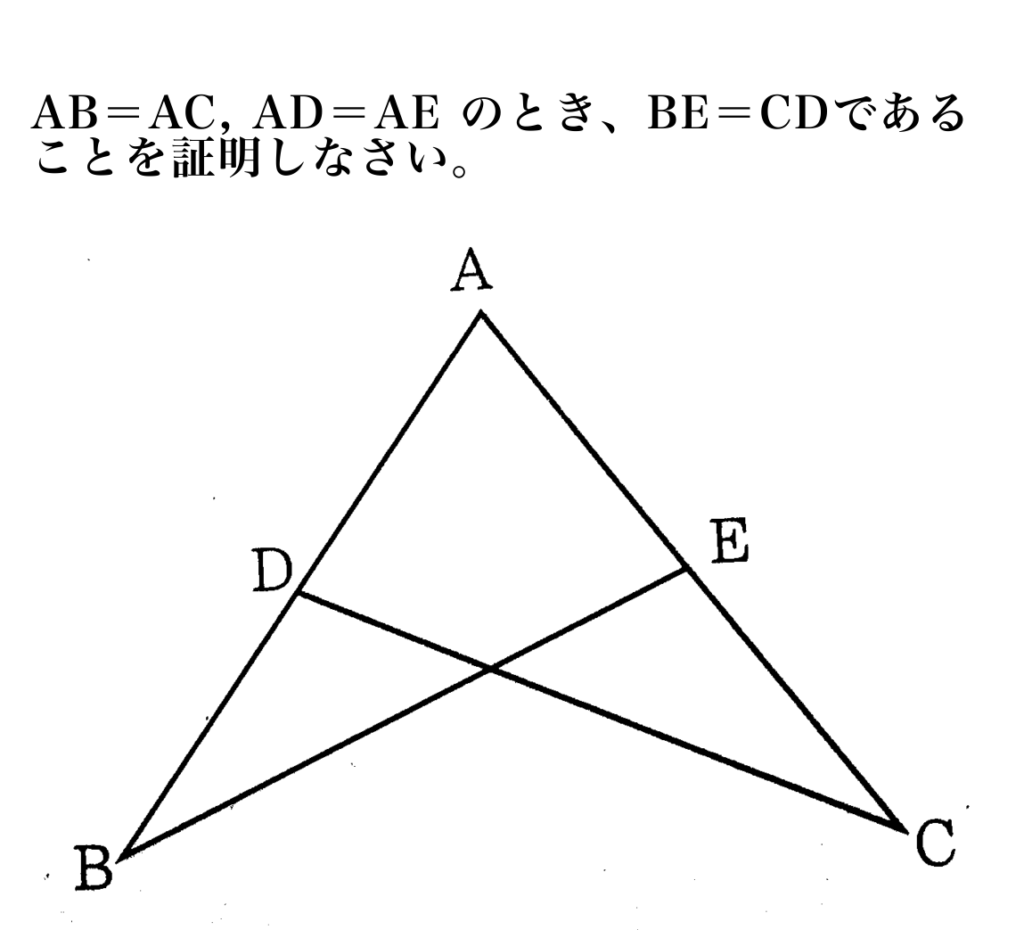
例題としてこの問題を証明してみましょう。
三角形の合同の証明 大まかな書き方
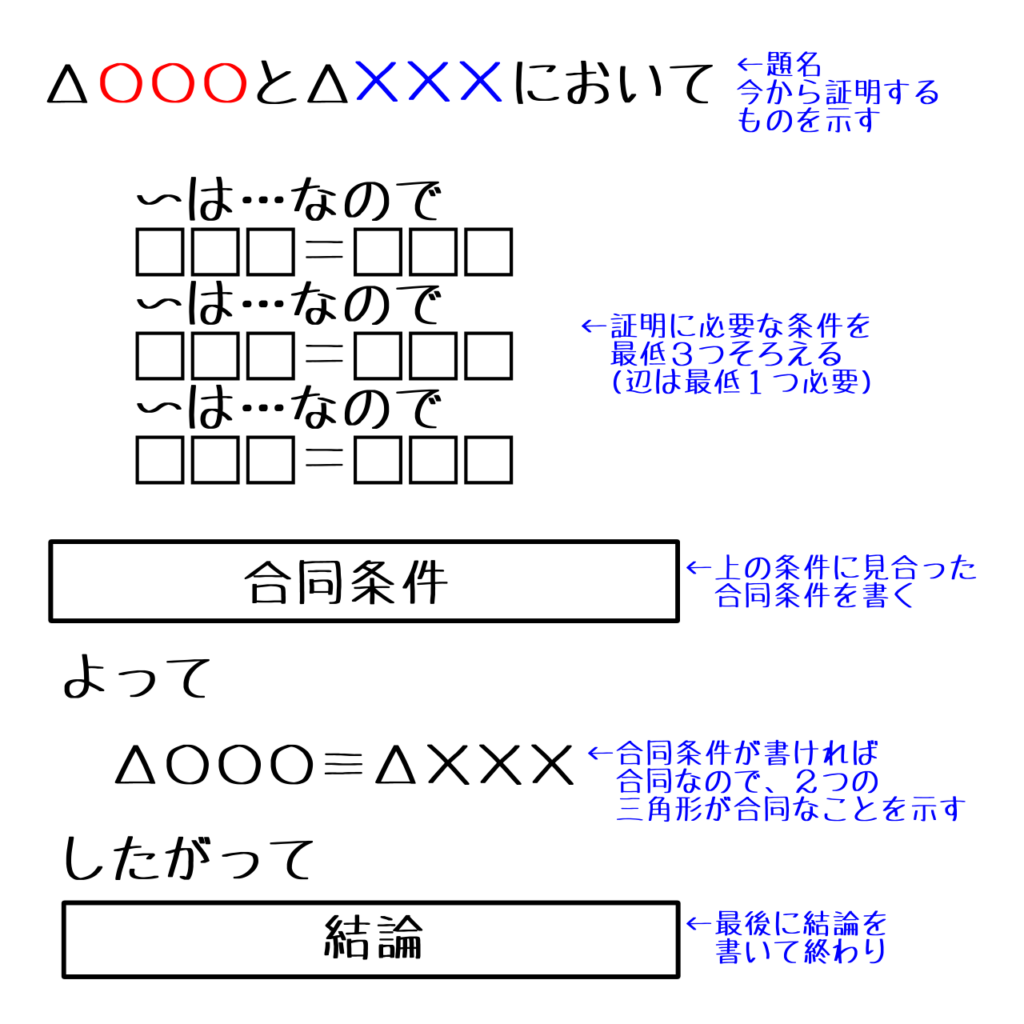
基本的な書き方はこんな感じです。各段落ごとに説明をしていきます。
見出し(題名)部分の書き方
今から合同を証明する2つの三角形を書きます。

この問題を例に説明します。
この問題で合同を証明したい三角形は、△ABEと△ACDです。なので、
△ABEと△ACDにおいて
と書くところからスタートします。
ここでの注意点!
①必ず対応する辺の順番に書くこと
もし、始めを△AEBとしたのなら、後ろも△ADCの順番で書きます。
②△ABE≡△ACDにおいて⇐このように書かないように注意!
これから合同を証明するので、まだ合同とは決まっていません。記号「≡」でつながないようにしましょう。
条件部分の書き方
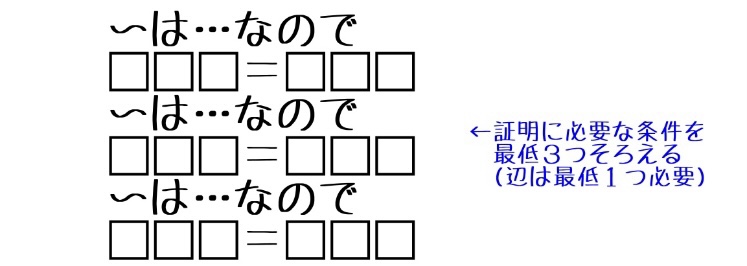
ここの書き方は、学校での習い方が大きく分けて2つあるようです。
①条件の根拠を( )の中に書く
例:〇〇=〇〇(仮定)
②条件の根拠を文章で書く
例:仮定より 〇〇=〇〇
まず、「①条件の根拠を( )の中に書く」の方から書き方を説明していきます。
①条件の根拠を( )の中に書く場合の条件の書き方

△ABEと△ACDにおいて
AB=AC(仮定)
AD=AE(仮定)
このように、まずは問題文から分かることを挙げていきます。
通常の場合、問題文から分かる条件(仮定条件)は1~2つです。
しかし、合同を証明するためには最低3つの条件が必要になります。残りを問題文や図を見ながら自力で導いていかなければならないのです。
この問題の場合、2つの三角形が共に∠Aを使っています。
そうすると、3つ目の条件は∠BAE=∠CAD(共通)です。
ここまでをまとめましょう。
△ABEと△ACDにおいて
AB=AC(仮定)
AD=AE(仮定)
∠BAE=∠CAD(共通)
補足
この問題の場合は、∠Aと書いただけでもどの角を示しているのかが分かるので、「∠Aは共通」や「∠A=∠A(共通)」などの書き方をしても問題ありません。しかし、「∠BAE=∠CAD(共通)」のように、どの辺とどの辺に挟まれた角なのかを明示した方が無難です。
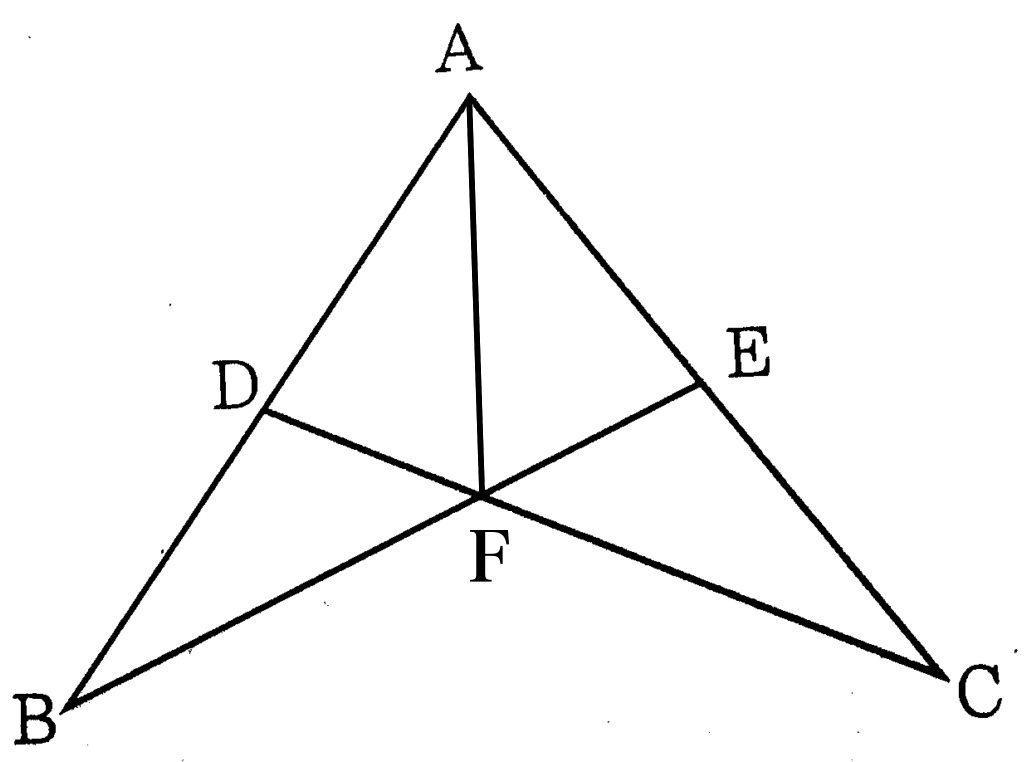
なぜかというと、例えばこのような図になっている場合だと、∠Aと表記しても、∠BAFも∠CAFも∠BACも全部∠Aなので、どれのことを言っているのか分からないからです。
つまり、「∠BAE」のように書けばどんな場合にも通用する、ということですね。
②条件の根拠を文章で書く方法

△ABEと△ACDにおいて
仮定より
AB=AC
AD=AE
共通の角なので
∠BAE=∠CAD
このように、最初に同じである根拠(この証明では「仮定より」と「共通の角なので」)を明示して、分かった条件を書いていきます。
条件部分を書くときの間違い例

仮定より
AB=AC
AD=AE
BE=CD
BE=CDは仮定条件ではありません。今から証明する事柄です。
「~であることを証明しなさい」の「~」の部分は「条件」ではなく「結論」です。合同だと分かったあとで、「だからこれとこれは同じなんだよ」と言えることです。仮定条件のところに書かないように注意しましょう。
合同条件~合同であることの書き方


今まで分かったことから導かれる合同条件は
「2組の辺とその間の角がそれぞれ等しい」です。
そして、合同条件が成立すれば、2つの三角形は合同です。
ここまでの書き方はこのようになります。
条件を( )で書く場合
△ABEと△ACDにおいて
AB=AC(仮定)
AD=AE(仮定)
∠BAE=∠CAD(共通)
2組の辺とその間の角がそれぞれ等しいので
△ABE≡△ACD
条件を文章で書く場合
△ABEと△ACDにおいて
仮定より
AB=AC
AD=AE
共通の角なので
∠BAE=∠CAD
2組の辺とその間の角がそれぞれ等しいので
△ABE≡△ACD
結論部分の書き方

ここでは「したがって」としましたが、
「合同な図形の対応する辺(角)は等しいから」
と書いて、結論を書きなさい!…と指導されるかもしれません。
そのように言われたのであれば、その先生の流儀に従ってください。教科書にもそう書いてあるかもしれません。それに反抗して書かないで、期末テストとかで減点されるのももったいないですしね。
でも、一般的には「したがって」とか「よって」などのつなぎの言葉だけで結論を書いても全く問題ありません。
ちなみに、「合同な図形の対応する辺(角)は等しいから」を書く場合は、結論が辺なら「合同な図形の対応する辺は等しいから」と書き、
結論が角なら「合同な図形の対応する角は等しいから」
と書きます。
さて、最後までをまとめてみましょう。
条件を( )で書く場合
△ABEと△ACDにおいて
AB=AC(仮定)
AD=AE(仮定)
∠BAE=∠CAD(共通)
2組の辺とその間の角がそれぞれ等しいので
△ABE≡△ACD
したがって(合同な図形の対応する辺は等しいから)
BE=CD
条件を文章で書く場合
△ABEと△ACDにおいて
仮定より
AB=AC
AD=AE
共通の角なので
∠BAE=∠CAD
2組の辺とその間の角がそれぞれ等しいので
△ABE≡△ACD
したがって(合同な図形の対応する辺は等しいから)
BE=CD
これで終了です。
「条件を( )に書く方法」と「文章で書く方法」のメリット・デメリット
条件を( )に書く方法のメリット
〇長い文章を書かなくて良いので楽
〇何を書いたら良いか分からない場合はまとめやすい
条件を( )に書く方法のデメリット
〇( )の中に単語1つで収まらない条件の場合は書きにくい
〇解答・解説の書き方はだいたい文章で書く書き方で説明がされているので解答を見たときに「これでいいのかな?」と思ってしまったりする。
文章で書く方法のメリット
〇( )に制限されることなく自分の考えた根拠を説明しやすい
〇解答・解説の書き方はだいたい文章で書く書き方で説明がされているので、間違った場合に違いが分かりやすい
文章で書く方法のデメリット
〇( )書きだけで済むような条件のときには文字数や行数が多くなる分わずらわしく感じる
〇証明を学びたての人はどう書けばいいのか分からなくなりがちなので、扱いにくいことがある
どちらの方法もメリット・デメリットはあります。証明のしかたを学びたての人には、( )書きの方が分かりやすいかもしれません。どんな証明でも、三角形の合同の証明ならこのテンプレで収めることが不可能ではないので。それに、学校で先生がそう教えるのであれば、それに従った方が良いでしょうし。
しかし、私は文章で書く方が後々になって楽になるのではないか、と感じています。そう感じる理由は次の2点です。
①難しい証明になればなるほど( )内に収まるような簡単な理由で説明できるものばかりではなくなる(カッコ内で収めることの方がわずらわしくなる)。
②これから様々な証明問題を解いていく上でいつまでもテンプレに頼ってばかりはいられなくなる(文章で書く練習をしていた方が自由度があって書きやすくなる)
現に、中2で学習する「平行四辺形になることの証明」は三角形の合同の証明テンプレートで証明できるものではない場合が多いです。
しかし、証明の書き方に慣れる手段としてはカッコ書きでの証明も悪くはありません。それを自分なりに発展させていけばそれで良いと思います。
証明において大事なのは、どこが同じなのかを理論的に理解し、理路整然と言葉と式でまとめることです。それができれば、書き方の手法がどうであろうと構わないと私は思います。


コメント