簡単な解き方&必要スキル
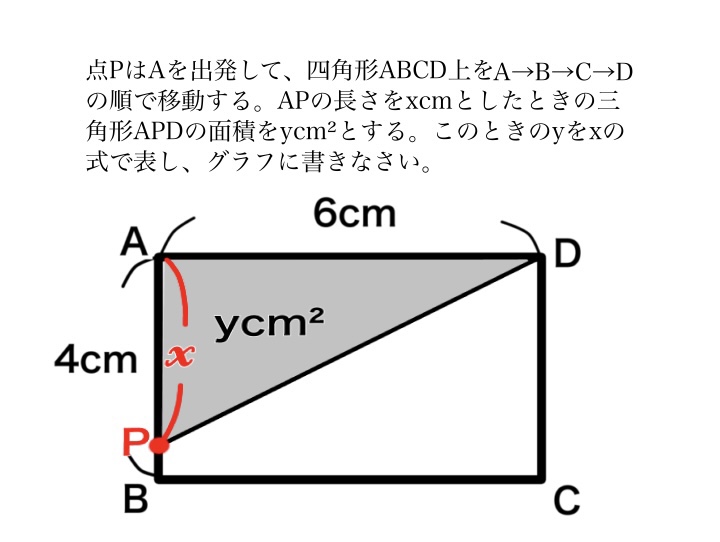
難しそうに見える問題ですが、実は点Pが各頂点にあるときの面積を出してグラフに書けば答えは出せちゃいます。
簡単な解き方
①点Pが各頂点(A、B、C、D)にあるときの面積を出してグラフを書く!
②そのあと直線の式を求める
この解き方に必要なスキル
一次関数の式を求めることができる!
逆に言えば、それさえできれば普通に解ける問題です。以下に説明します。
自信のない方はこちらをご覧ください。
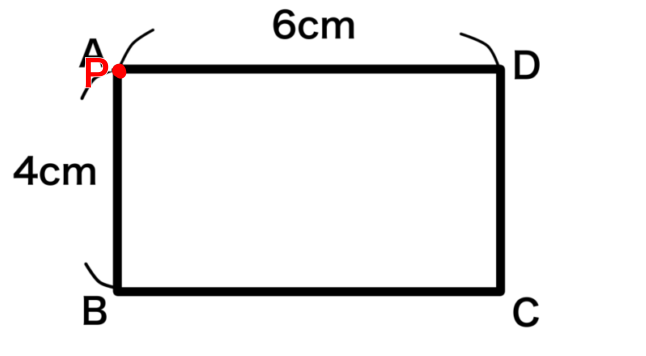
点Pが点Aにあるとき
APの長さは0cmなので、\(x=0\)
⊿APDの面積は0cm²なので\(y=0\)
座標が分かったので(0,0)に点をとります。
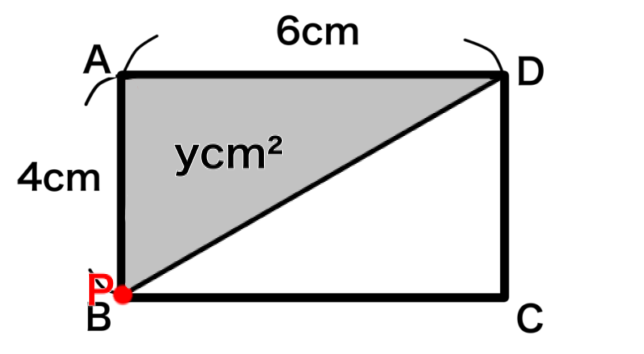
点Pが点Bにあるとき
APの長さは4cmなので、\(x=4\)
⊿APDの面積は
三角形の面積=底辺×高さ÷2より
6×4÷2=12
12cm²なので\(y=12\)
座標が分かったので(4,12)に点をとって線を引きます。
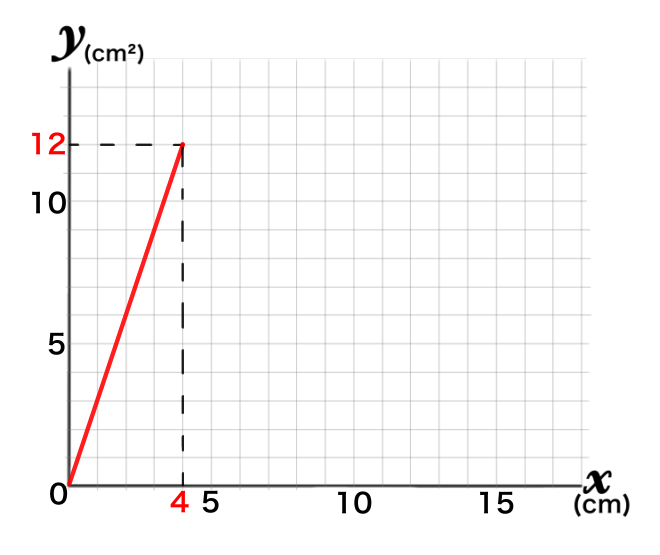
点Pが点Cにあるとき
APの長さは10cmなので、\(x=10\)
⊿APDの面積は
三角形の面積=底辺×高さ÷2より
6×4÷2=12
12cm²なので\(y=12\)
座標が分かったので(10,12)に点をとって線を引きます。
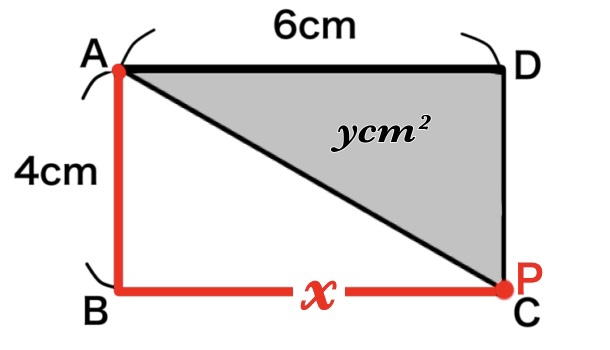
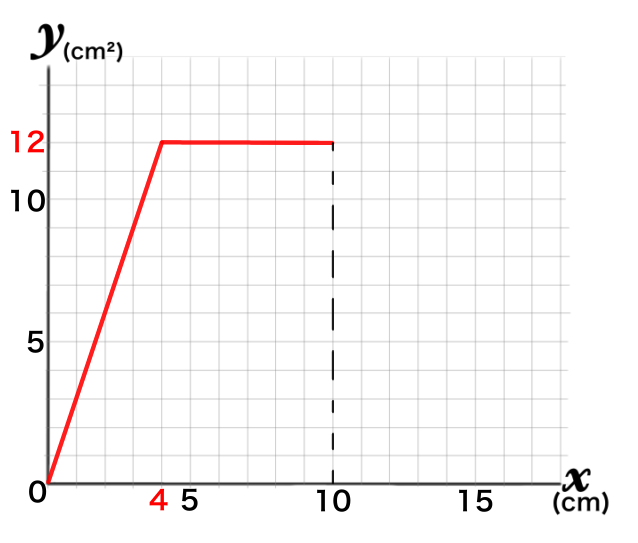
点Pが点Dにあるとき
APの長さは14cmなので、\(x=14\)
⊿APDの面積は
PとDが重なっているので面積は0cm²。
\(y=0\)
座標が分かったので(14,0)に点をとって線を引きます。
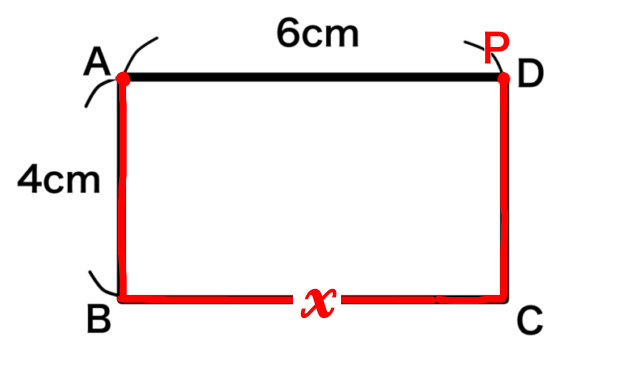
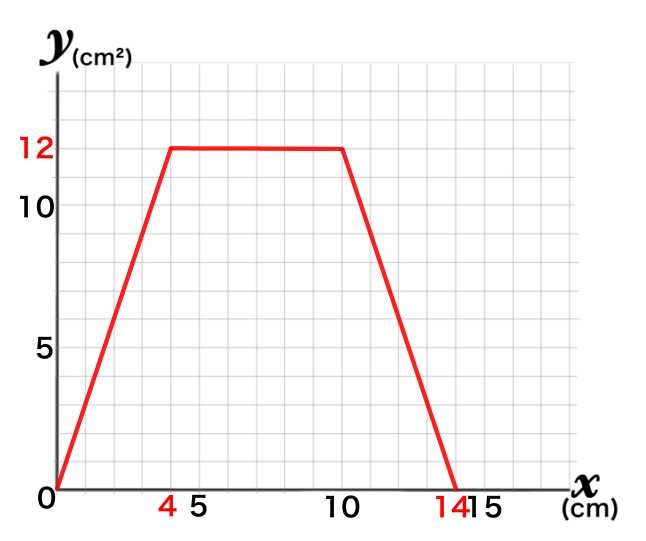
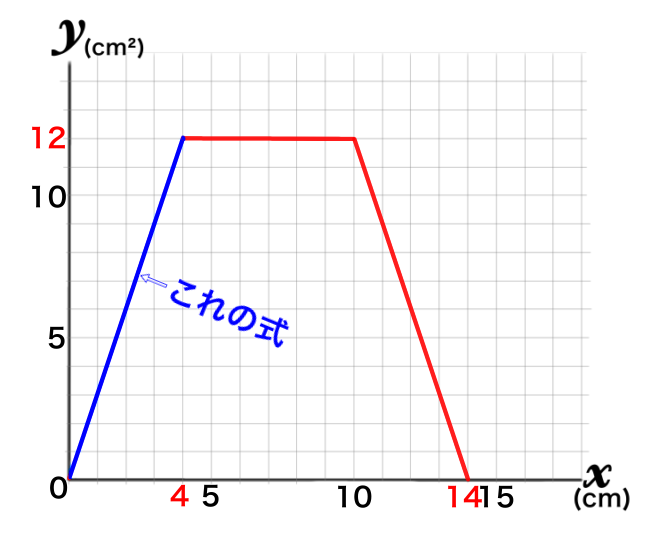
グラフができたので、グラフの式を求めます。
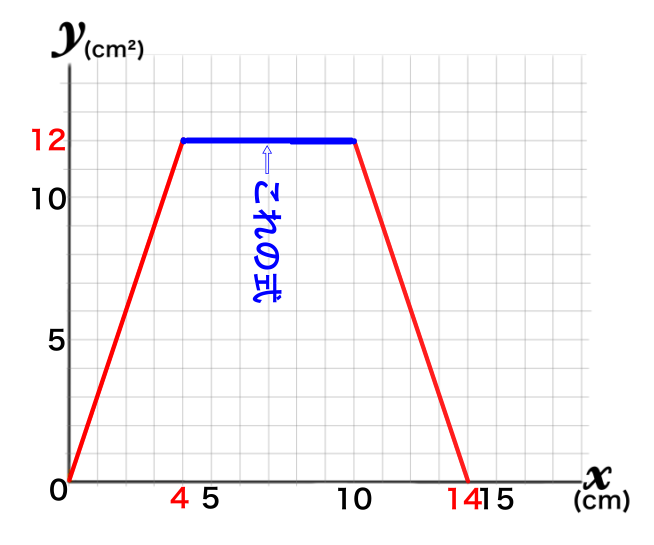
\(4\leqq x\leqq 10\) のとき
グラフはずっとy座標が12なので
\(y=12\)
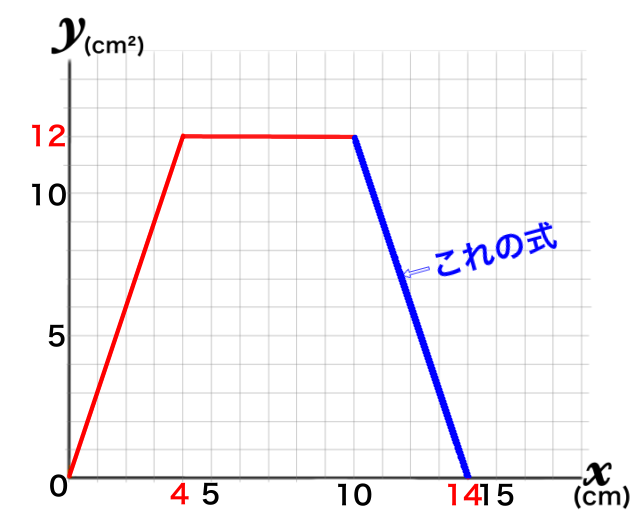
\(10\leqq x\leqq 14\) のとき
グラフ2点(10,12)(14,0)を通るので
\(y=ax+b\) に代入して
\(10a+b=12\) …①
\(14a+b=0\) …②
この2つを連立方程式で解くと②-①より
\(4a=-12\)
\(a=-3\)
①に代入して
\(10\times \left( -3\right)+b=12\)
\(b=12\)
よって
\(y=-3x+42\)
答えのまとめ
\(0\leqq x\leqq 4\) のとき\(y=3x\)
\(4\leqq x\leqq 10\) のとき\(y=12\)
\(10\leqq x\leqq 14\) のとき\(y=-3x+42\)
グラフ

このように考えても解けます。各分岐点の座標さえ分かればグラフは書けるので、それを読み取れば式も出せる!
普通の方法と解き方が反対ですが、考え方はこれが一番楽だと思います。
でも、やっぱり普通の解き方、考え方も紹介しますね⇩
普通の解き方 解くための準備段階:イメージしましょう
次に挙げる準備をしておくと、その後の展開が断然楽になります。まずはイメージしてそれを図に書き留めておきましょう。
3つの三角形パターン
この問題には3つのパターンがあります。
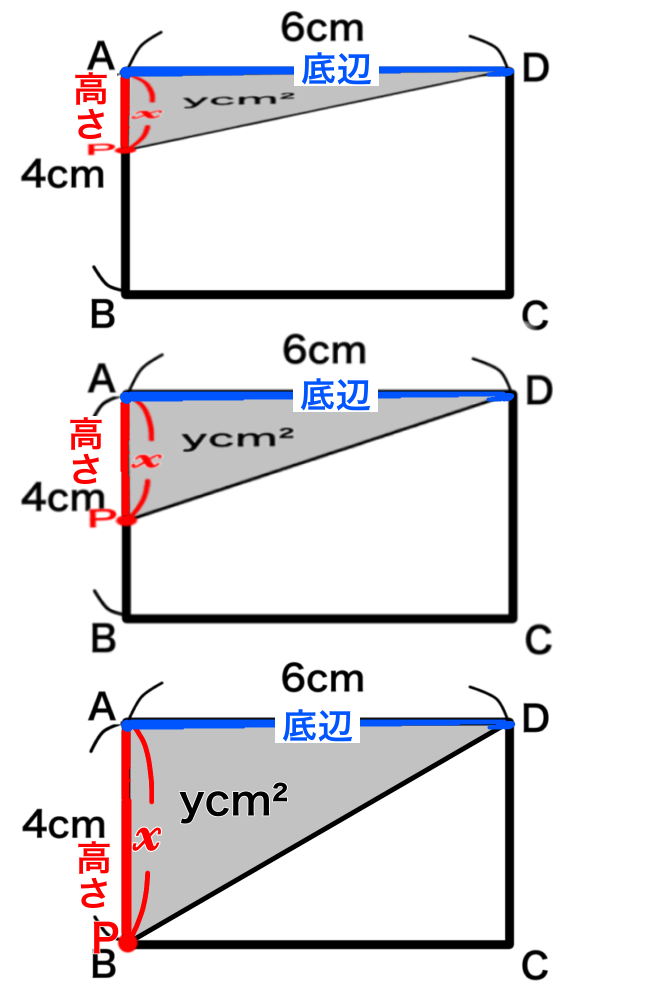
点PがAB上にあるときは、ADを底辺とすると、APが高さになる直角三角形になります。
そして点Pがどれだけ進んでも、APの長さが\(x\) と定められているので、高さは\(x\) のままです。
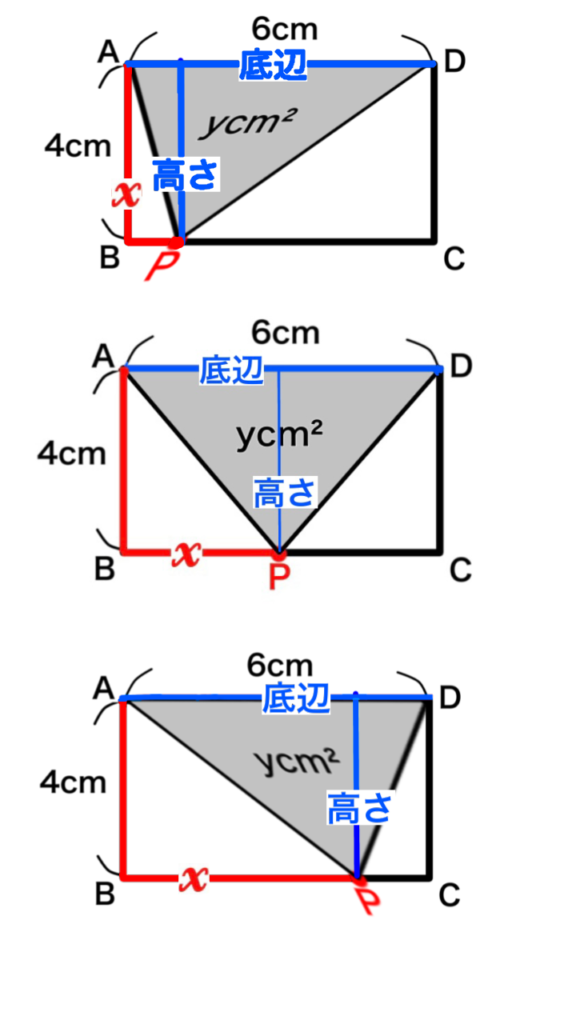
点PがBC上にあるときは、このような三角形になります。
点PがBC上のどこにあっても、底辺も高さも同じであることが分かります。
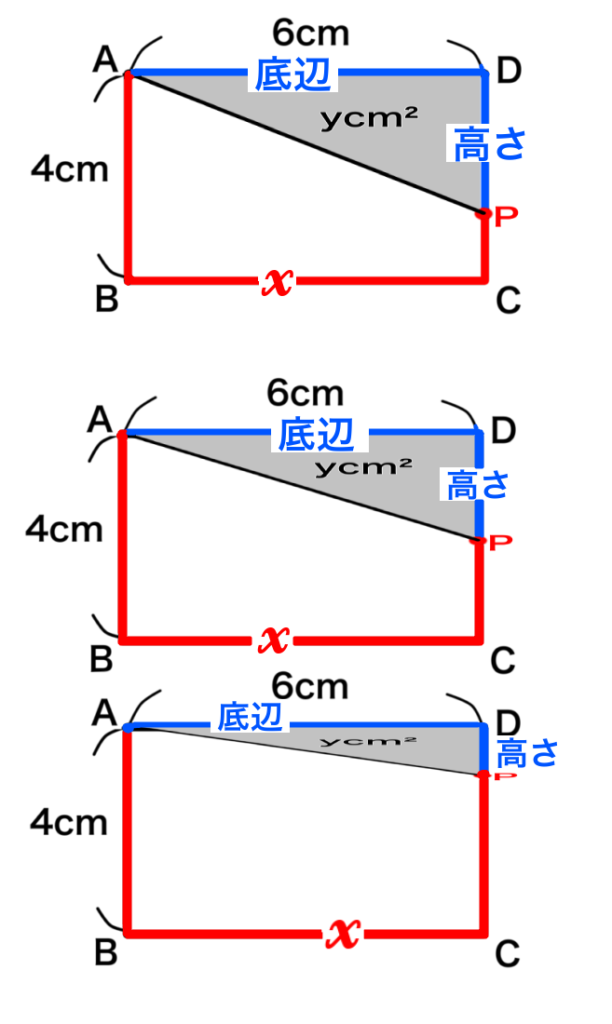
点PがCD上にあるときは、ADを底辺とすると、DPが高さになる直角三角形になります。
点Pが点Dに近付いていくと三角形の面積が小さくなっていくことが分かります。
場面のかわるこの3パターンに分けて面積\(y\) を式で出していくことになります。
点PがAB上にあるとき
変域を確認しよう
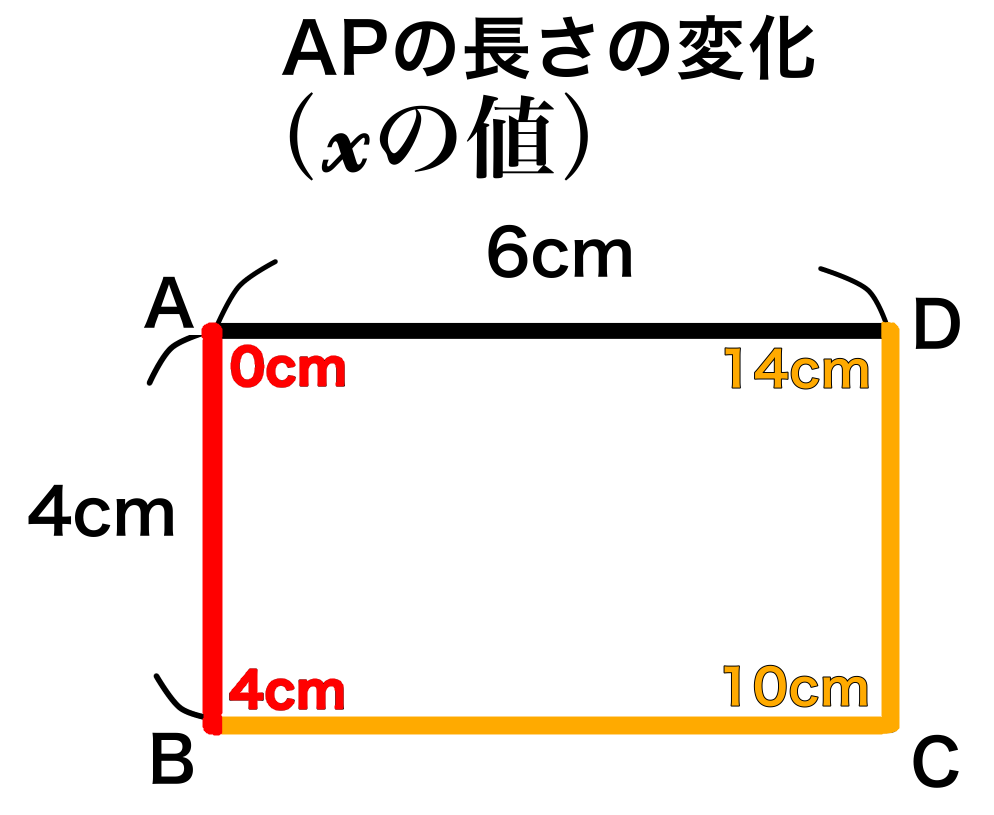
点PがAB上にあるということは、図のように点Pが点Aを出発してから動く範囲は0~4cmの間です。
つまりAPの長さ\(x\)の変域は\(0\leqq x\leqq 4\)となります。
式を求めよう
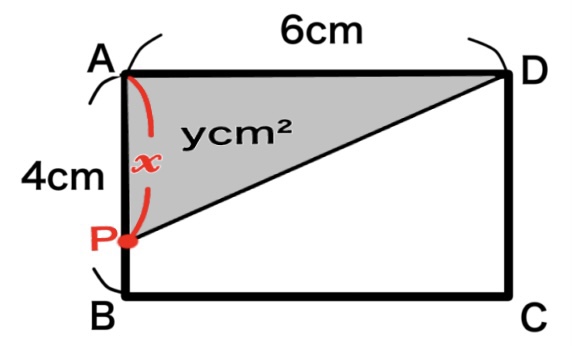
問題文からAPの長さは\(x\) です。
AB上に点Pがあるのは\(x\) の変域:\(0\leqq x\leqq 4\)のときです。
底辺を6cmとすると高さは\(x\) cmなので、三角形の面積は\(y\) なので公式に当てはめます。
三角形の面積=底辺×高さ÷2
\(y=6\times x\div 2\)
\(y=3x\)
よって、\(0\leqq x\leqq 4\)のとき\(y=3x\)
ここまでのグラフを書いてみよう
\(x\) が0~4の間で\(y=3x\) のグラフを書きます。
\(x\)が4までで止めて下さいね!
\(x\)が4のとき、\(y=3x\) に代入すると、
\(y=3x=3\times 4=12\) なので点(4,12)に点を取って、(0,0)からまっすぐに線を引きます。
そうするとこうなります↓

点PがBC上にあるとき
変域を求めよう
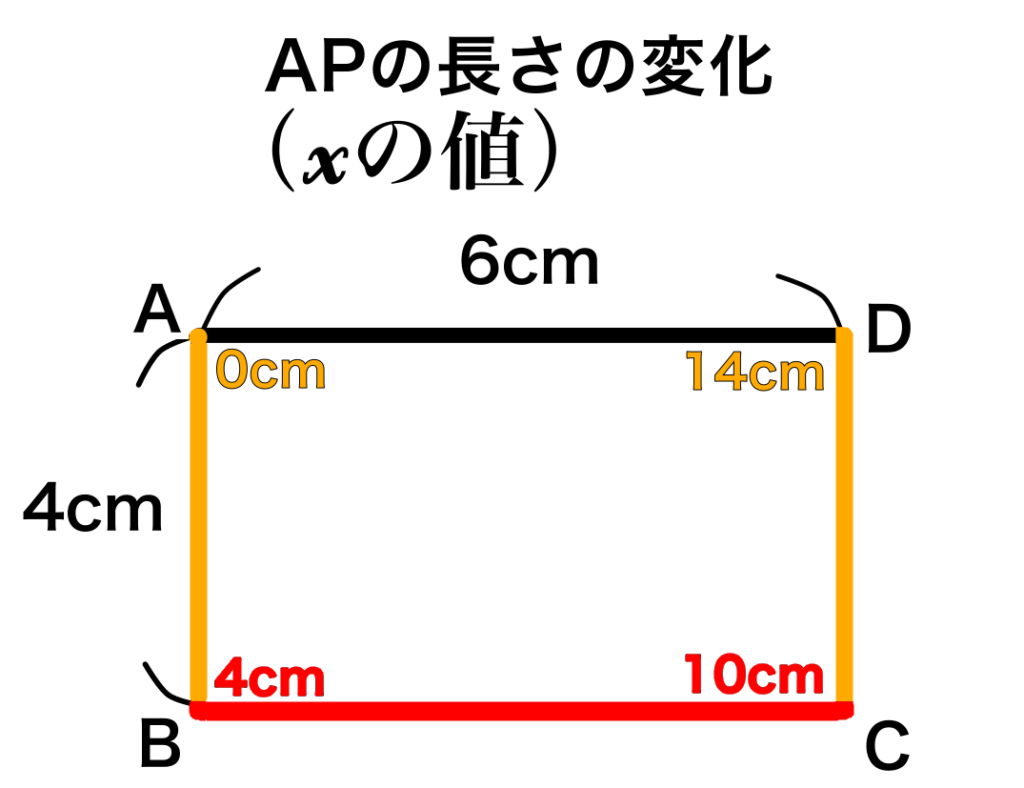
点PがBC上にあるということは、図のように点Pが点Aを出発してから4~10cm移動したときです。
つまりAPの長さ\(x\)の変域は\(4\leqq x\leqq 10\)となります。
式を求めよう
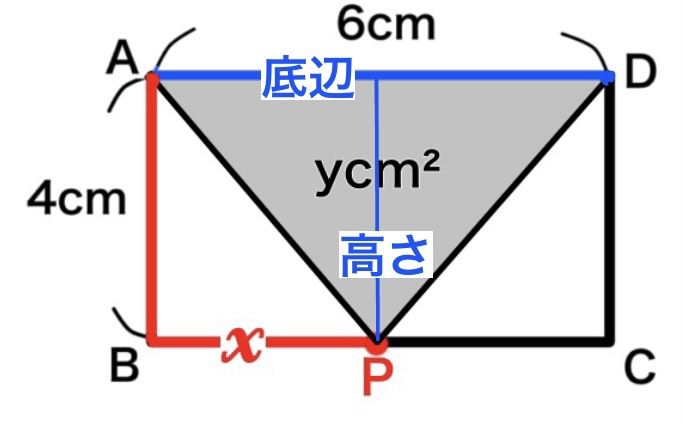
\(x\)はAPの長さなので図の赤線部分になりますが、三角形の面積は底辺と高さで決まるので、この場合\(x\) の値は関係なくなります。
底辺は6cm、高さは4cmになるので、三角形の面積\(y\)はこのようになります。
\(y=6\times4\div 2\)
\(y=12\)
BC上に点Pがあるのは、\(x\) の変域:\(4\leqq x\leqq 10\) のときです。
よって、\(4\leqq x\leqq 10\) のとき\(y=12\)
ここまでのグラフを書いてみよう
\(x\) が0~4で書いた\(y=3x\) のグラフの続きに書きましょう。
\(x\)が4~10までの間は、面積は12のままです。
だからこうなります↓

点PがCD上にあるとき・高さの出し方テクニック
変域を求めよう
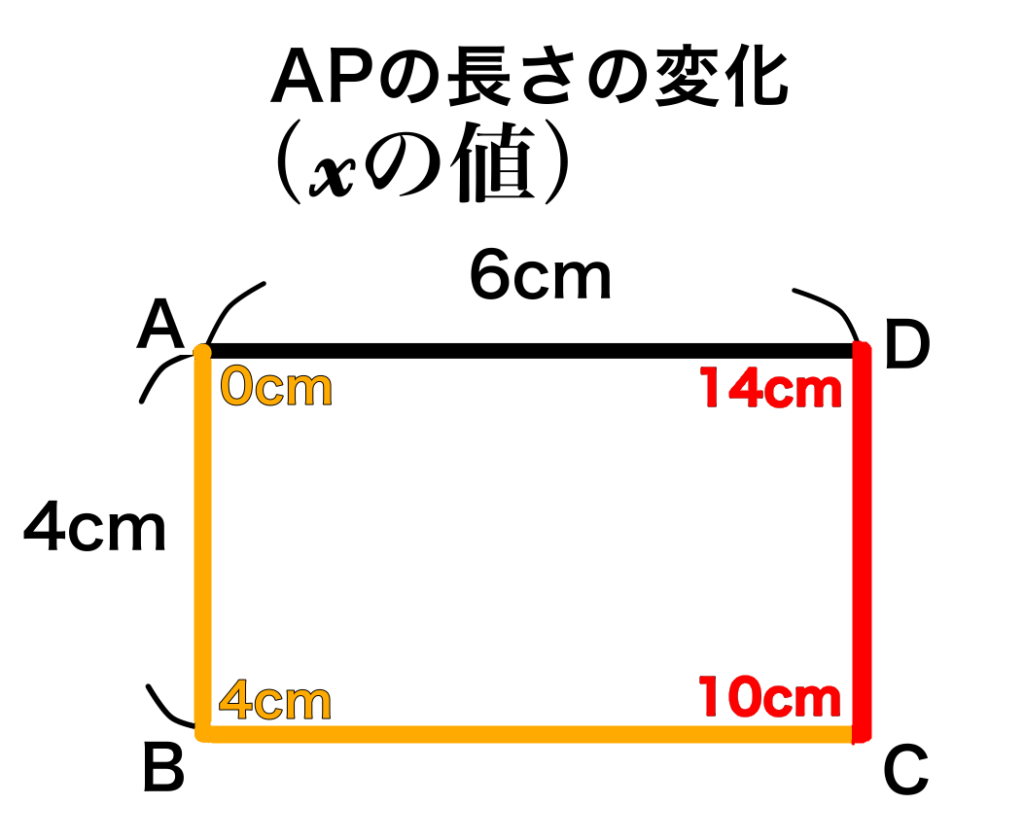
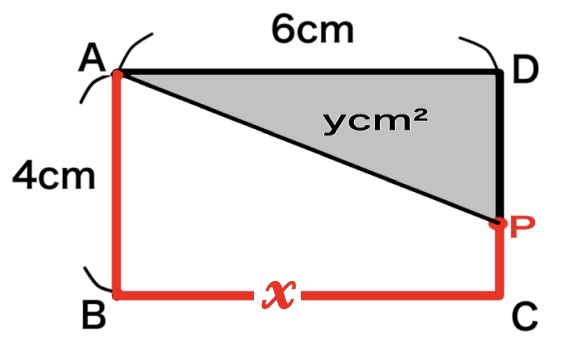
点PがCD上にあるということは、図のように点Pが点Aを出発してから10~14cm移動したときです。
つまりAPの長さ\(x\)の変域は\(10\leqq x\leqq 14\)となります。
式を求めよう
…の前に高さは何センチ?

このとき、底辺は6cmでOKです。
この場合も高さを\(x\) としてしまいがちですが、それは間違いです。

え?だって、高さが分からないんだもん!
分からないから\(x\) でいいじゃん!

APの長さを\(x\) にしているから、高さで\(x\)は使えないんじゃないでしょうか?

そっかぁ。じゃあ、高さは\(y\) ?

\(y\) は面積になってしまうでおじゃる。
\(x\) を使って高さを表すのじゃ。
底辺を6cmとしたときの高さはここです!
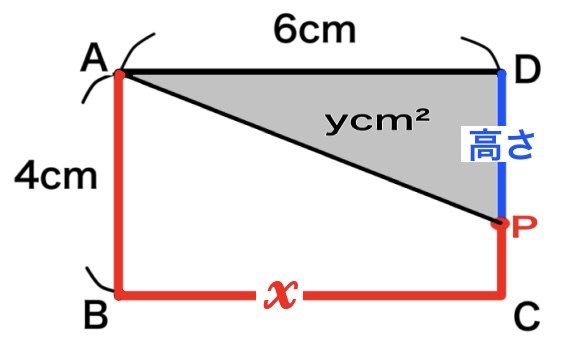
青線で示した部分PDの長さが高さになります。ここが何cmなのかを求めなければなりません。

はぁ?\(x\) を使って高さを表すって何?
無理じゃね?想像もできない。
高さの出し方テクニック
なぜ分かりづらいかというと、\(x\)が曲がっているからなのです。
無理やりまっすぐにして考えましょう。
ということで、点Pの道筋をまっすぐにしておりますのでしばらくお待ちください。
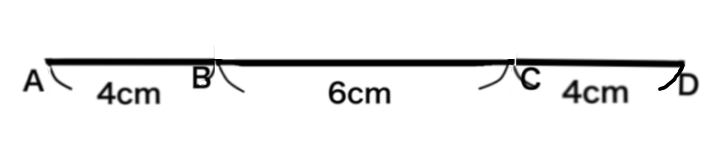
で、まっすぐになったので説明します。
点PはCD上にあります。そしてAPの長さが\(x\)です。
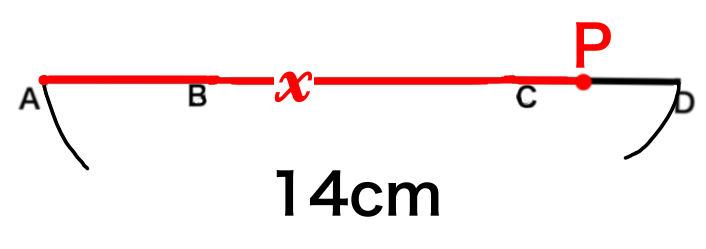
そうすると、PDの長さは、全体の14cmから、\(x\)を引いた値になりますので、
\(PD=14-x\)
となります。
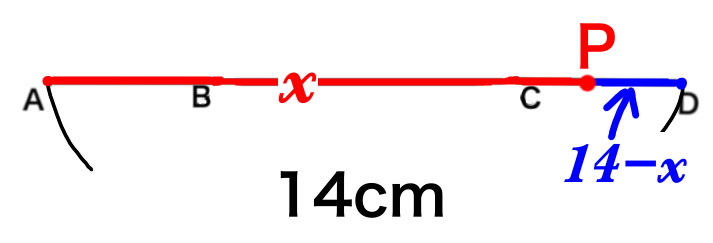
つまり、三角形はこうなります。
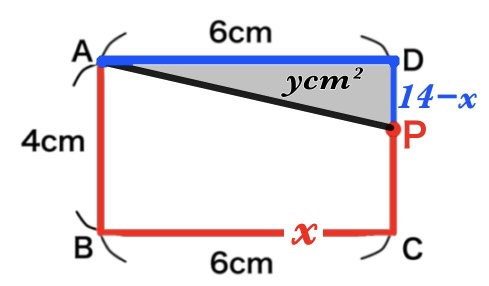
そうすると底辺6cm、高さ\(14-x\)cmなので、面積\(y\) は
\(y=6(14-x)\div 2\)
\(y=3(14-x)\)
\(y=42-3x\)
一次関数っぽく並べると
\(y=-3x+42\)
ここまでのグラフを書いてみよう
今までのグラフの続きに書きましょう。
\(10\leqq x\leqq 14\)のとき\(y=-3x+42\)でした。

切片42!ヤバッ!
どうやって書くの??
などと思われがちですが、全然大丈夫です。
\(x\) が10~14のときだけのグラフです。
\(x=10\)のときと\(x=14\)のときを式に入れて計算すれば座標が出るので、それをつなげばよいのです。
\(x=10\)のとき
\(y=-3\times 10+42=-30+42=12\)
つまり、(10,12)を通るので…

あ、ここから始まればいいってことですね。
\(x=14\)のとき
\(y=-3\times 14+42=-42+42=0\)
つまり、(14,0)を通るので、点を取って線で結ぶと…

…と、こうなります。
これで全部解けました!
答えのまとめ
\(0\leqq x\leqq 4\) のとき\(y=3x\)
\(4\leqq x\leqq 10\) のとき\(y=12\)
\(10\leqq x\leqq 14\) のとき\(y=-3x+42\)
グラフ

これで全行程終了ですが、一応確認事項↓
一応確認事項
点Pが14cm進むということは、点Dと重なるわけですから
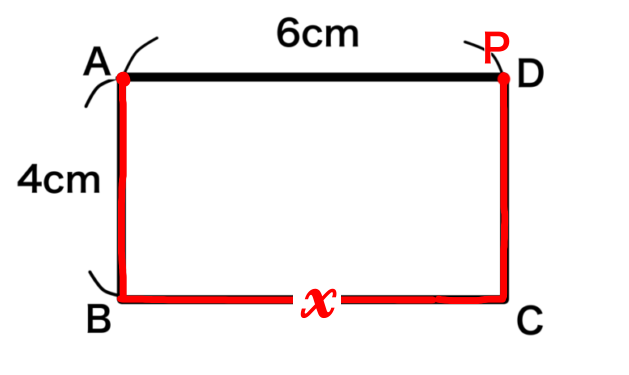
⊿APDは高さが0になるので面積0で当たり前ですね。
まとめ
2つの解き方を説明しました。どちらでも解けますので好きな方で解いてもらってよいと思います。ただ、学校で学習しているのは多分「普通の方」です。そこだけは注意しておいてくださいね!


コメント