一次関数の利用 ちょっと面白い日常生活?(自作)

三輪車で登校?どんな試みしとんねん!

三輪車には通学許可のステッカーが貼ってあるんでしょうか?

こんな感じの。貼ってないと校則違反ですよ。

そこが問題?ウケる!!

いや、問題はこの兄!
弟がバカやっているところを撮影しようとしてるって?
絶対SNS載せるつもりやろ!

うんうん。絶対やるね!
弟もそのために三輪車に乗って登校しようと思ったんじゃない?

その場合、ヘルメットは必要なんでしょうか?

そこが問題?ウケる!!
(1)の解き方 解答・解説
さて、真面目に問題をやっていきます。笑
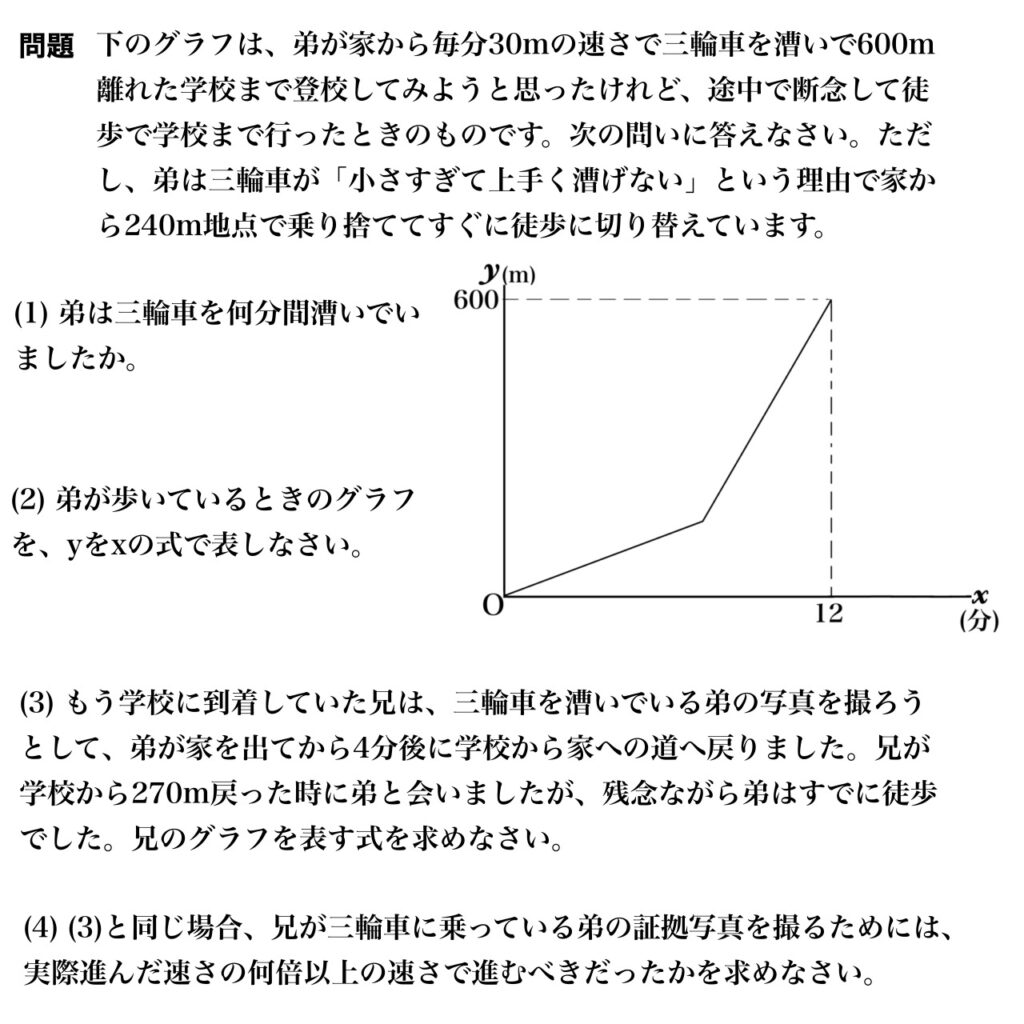
問題文を見ましょう。(前置き長すぎたのでもう一回貼ります)

「毎分30mの速さ」
「240m地点で乗り捨てた」
とあることから、乗っていた時間は導き出せます。
時間=道のり÷速さ なので
240÷30=8
答えは8分間
(2)の解き方 解答・解説
まずは、(1)で分かったことを図に書き込みましょう
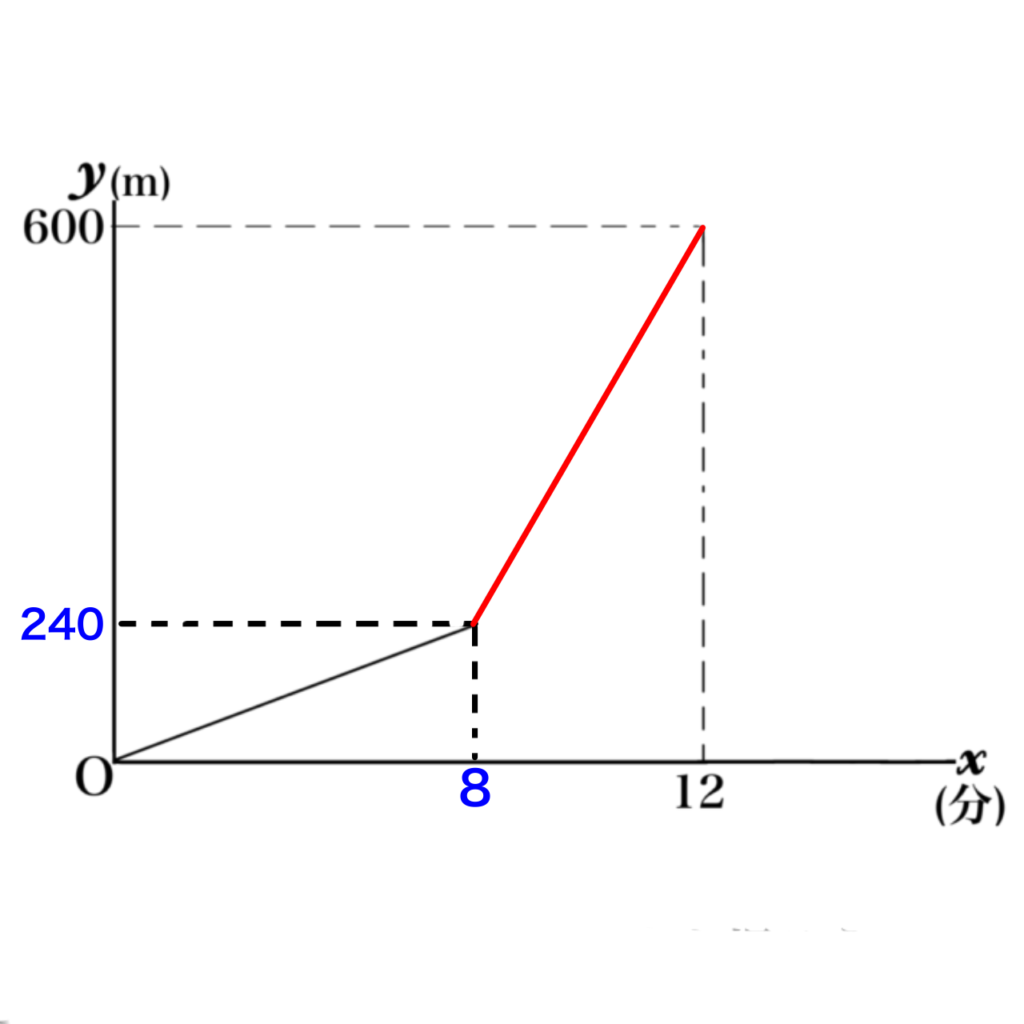
赤で示した線の式を求める問題です。この問題は難しそうに見えますが、基本がわかっていれば解ける問題です。

え!わかんない!

2点を通る直線の式の求め方が分かっていれば
この問題は解けるのじゃ
この記事の「例題4」を見るでおじゃる

2つ解き方があるやつ?
でも2つの点が分からないと解けないよ

それをグラフから読み取るのじゃ
基本問題と応用問題の違いはここです!
基本問題は「2点(2,-1)(5,-4)を通る直線の式を求めなさい」のように条件が与えられていますが、応用問題はこの2点をグラフから読み取らなければいけないのです。
でも、読み取ってしまえば基本と同じ解き方で解けます!
赤く塗った線の中で\(x\)座標も\(y\)座標も分かっている点が2つあるはずです見つけてみましょう!

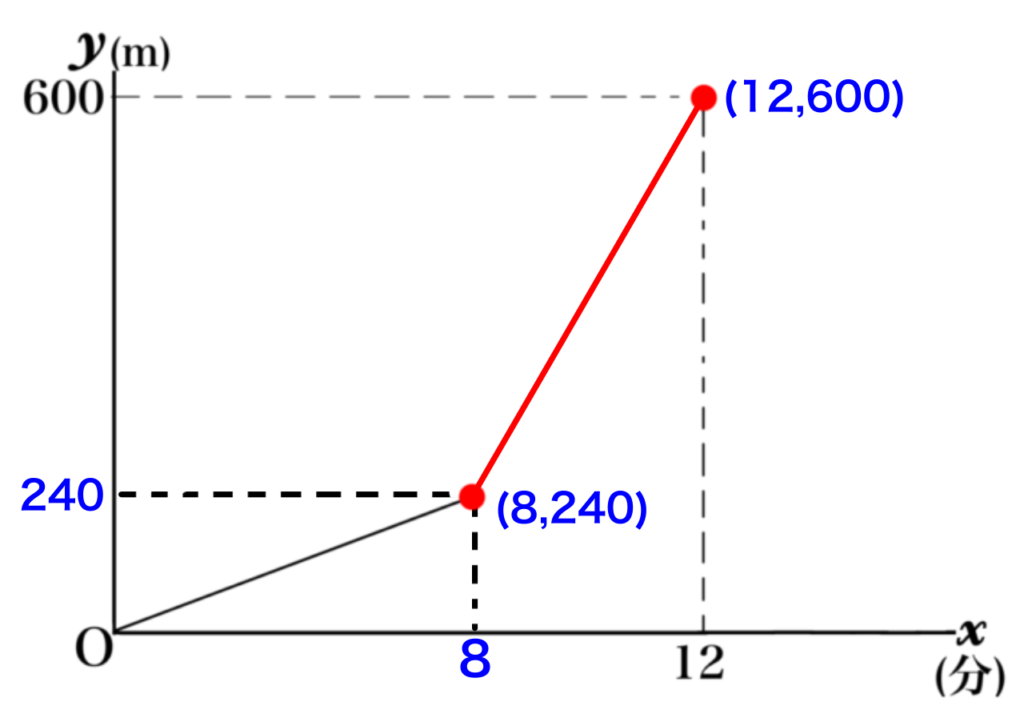
この2つ?
(8,240)(12,600)

それでおじゃる!
その2点を通る一次関数の式を求めれば良いでおじゃる。

え?そうなんだ!
じゃあ連立方程式で解こうっと♪
と、いうことでマイさんはこのように解きました。
\(y=ax+b\)に(8,240)と(12,600)をそれぞれ代入して2つの式を作ります!
まず(8,240)を代入して
\(240=a\times8+b\) だから、
\(8a+b=240\) ……①
次に(12,600) を代入して
\(600=a\times12+b\) だから、
\(12a+b=600\) ……②
②-①をして
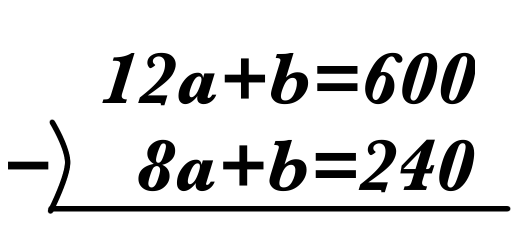
\(4a=360\)
\(a=90\)
①に代入して
\(8\times90+b=240\)
\(720+b=240\)
\(b=240-720\)
\(b=-480\)
\(y=ax+b\)に\(a=90\) と\(b=-480\)を代入して
\(y=90x-480\)

できた!正解?

正解でおじゃる!
と、こんな感じで解けます。
「座標を読み取って直線の式を求める」
これができるようになれば、それ以降の問題も解けるチャンスが広がってきます!
ここでは連立方程式を使いましたが、もちろん最初に傾きを求める方法でも解けます。
別解
(8,240)(12,600)この2点を通るから傾きは、
\(\dfrac{600-240}{12-8}=\dfrac{360}{4}=\)\(90\)
\(y=ax+b\) の\(a\)に\(90\)を代入して、
\(y=90x+b\)
(8,240)を通るから、\(x=8\),\(y=240\)を代入して、※((12,600)を代入してもOK!)
\(240=90\times8+b\)
\(b+720=240\)
\(b=240-720\)
\(b=-480\)
よって、\(y=90x-480\)
(2)の問題でよくやる間違い

「y座標が240からスタートしているグラフだから」という理由で
切片を240⇒\(y=ax+240\)
にしてしまう
切片は必ず「直線とy軸の交点」です。
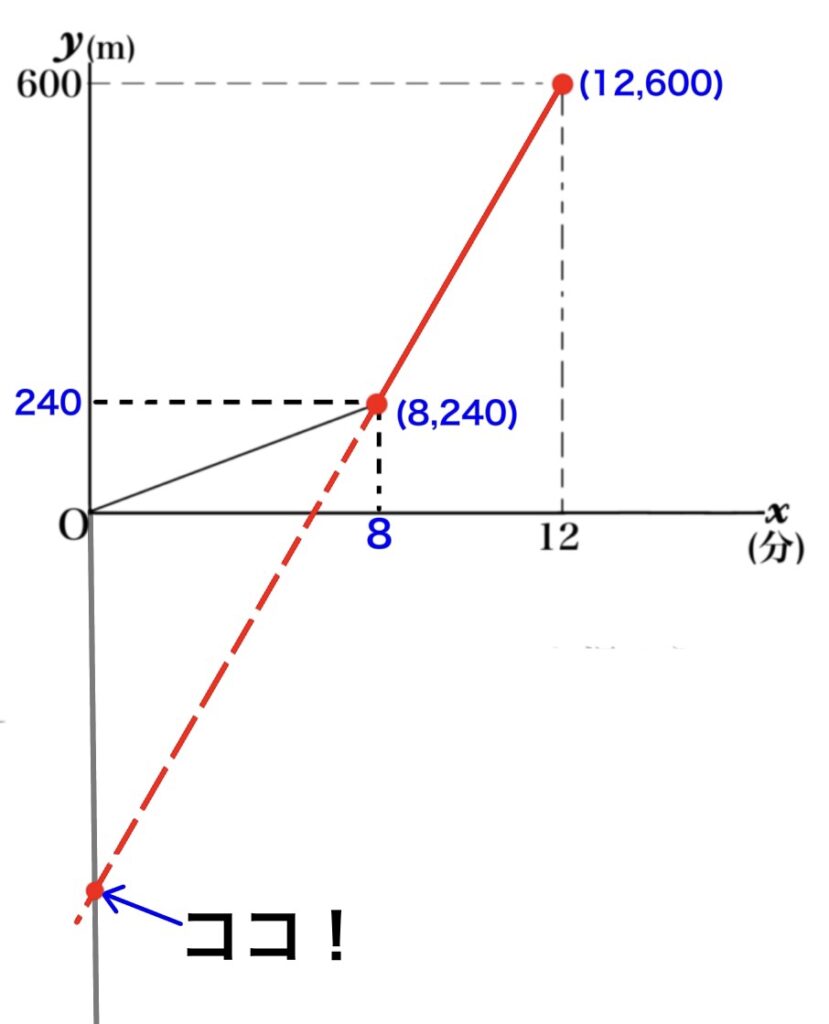
見た目では分かりにくいので、計算をして求めることになります。解くときには注意しましょう。
(3)の解き方 解答・解説

さて、ここからは読解が必要になります。
〇兄は学校に到着している⇒兄がいる地点は600m地点
〇弟が家を出てから4分後に学校から戻っている⇒兄が出たのは\(x=4\)のとき
つまり、(4,600)から兄のグラフは出現します。
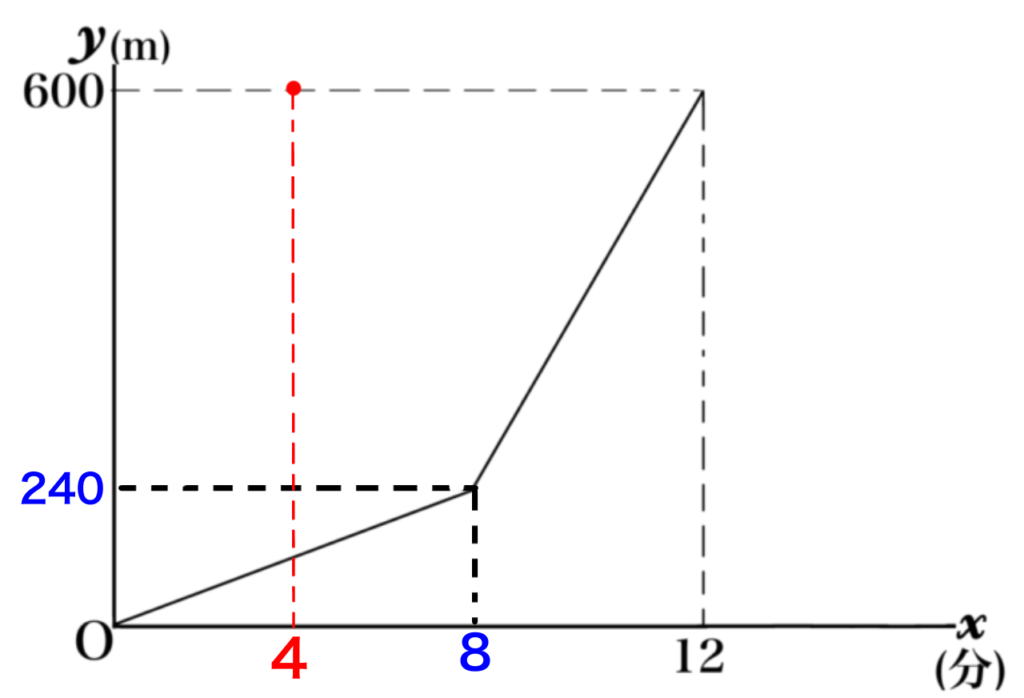
学校から270m戻っている⇒600-270=330
弟と会ったのは、グラフの330m地点です。
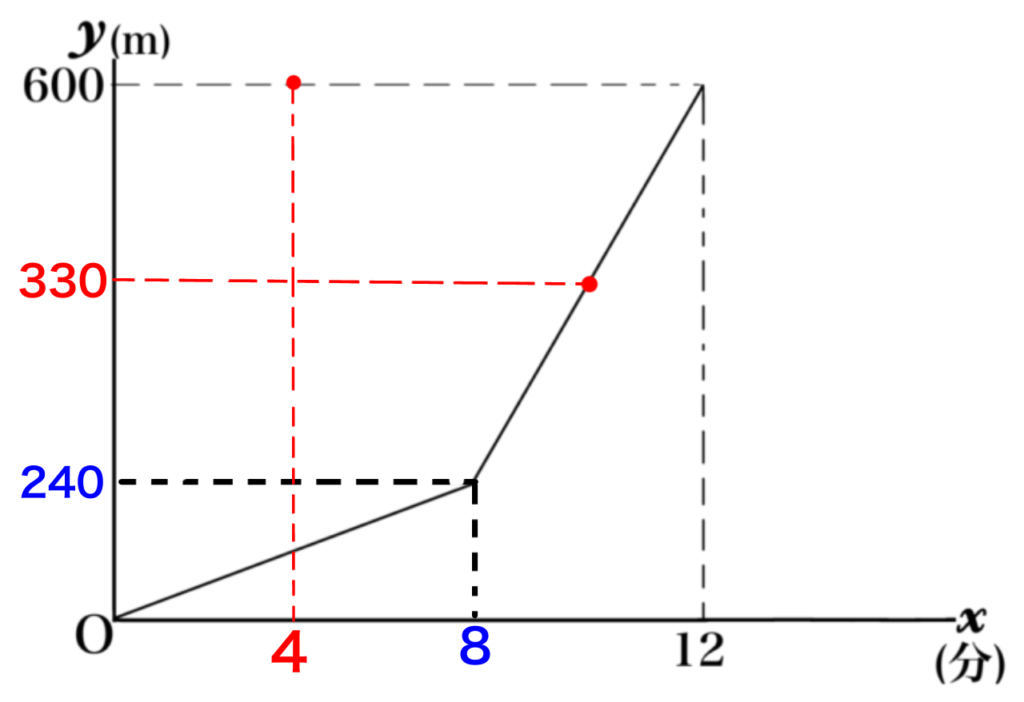
この2点を結んだ直線が、兄のグラフになります。
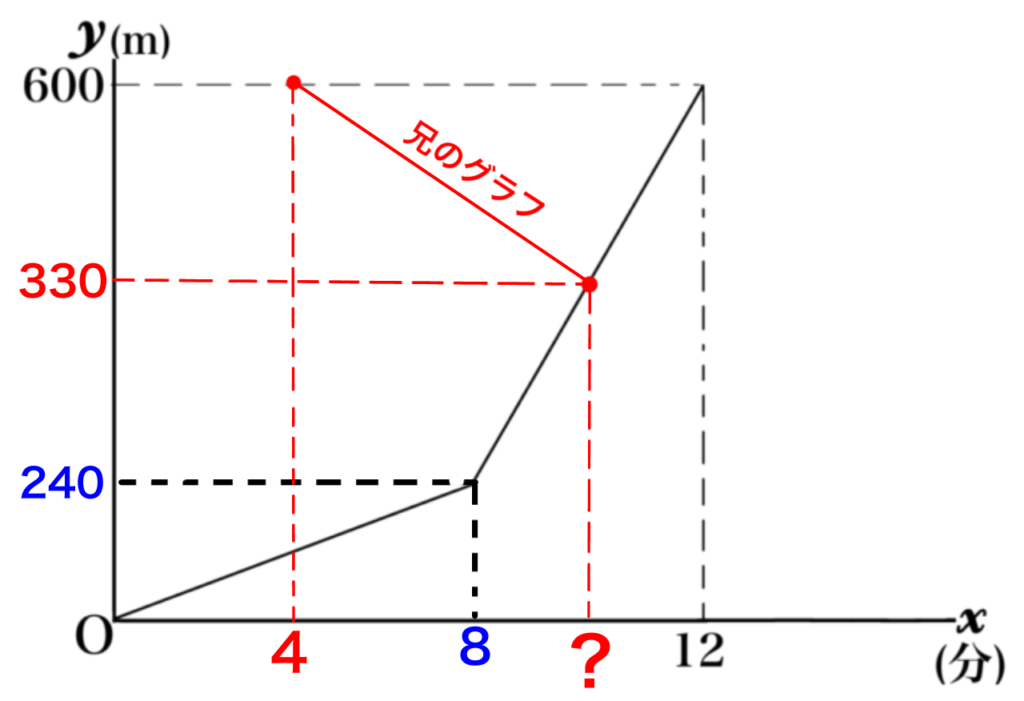
でも、直線の式を出すには、傾きや切片が分からない限り2つの点の座標が必要です。
(4,600)は分かっていますが、もう1点必要です。
そのためには、?の座標を知る必要があります。
グラフをよく見ると、(?,330)の点は、さっき問題(2)で出した直線の式、
\(y=90x-480\) 上の点ではないですか!
グラフ上の点は、必ず式の条件を満たします。
つまり、\(y=330\)を直線の式\(y=90x-480\) に代入すれば\(x\)座標は出てきます!
\(330=90x-480\)
\(90x-480=330\)⇐右辺と左辺を逆にしただけです。
\(90x=330+480\)
\(90x=810\)
\(x=9\)
ということは、?は9です!
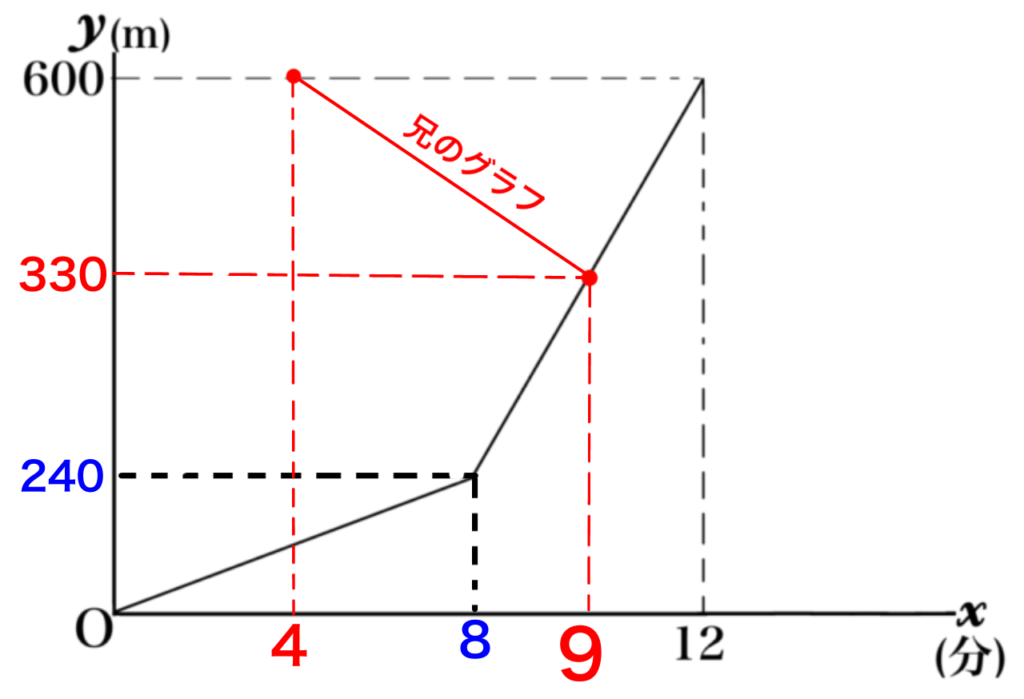
そうすると、兄のグラフは2点(4,600)(9,330)を通る直線です。ここまで分かれば、(2)の問題と同じです。連立方程式で解くか、傾き(変化の割合)を出してから求めるか、どちらかで求められます。
連立方程式で求める場合
\(y=ax+b\)に(4,600)(9,330)それぞれを代入していきます。
(4,600)を代入すると
\(600=4a+b\) ⇒\(4a+b=600\) …①
(9,330)を代入すると
\(330=9a+b\) ⇒\(9a+b=330\) …②
②-①で連立方程式(加減法)をしましょう。
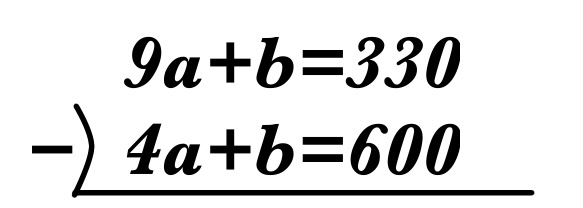
\(5a=-270\)
\(a=-54\)
①に代入します。
\(4\times\left( -54\right)+b=600\)
\(-216+b=600\)
\(b=600+216\)
\(b=816\)
よって、\(y=-54x+816\)
これで正解!!
…なのですが、こんな数が出てきたら
「え?間違ってる?」
と思って、計算し直したり、自信がなくて答えを消しちゃったりする人もいますよね!
そこで用いたいのがこれ!
「答えが正しく出ているらしい?をだいたい判断できる方法」
以下を参考にして下さい。
一次関数の応用問題で「答えが正しく出ているらしい?」をだいたい判断できる方法
【①傾きの符号が正しいかどうか判断する】
右上がり⇒傾きは+、右下がり⇒傾きは-
符号ミスはしやすいので、第一に確認しておきましょう。
【②傾きの数字が多分正しい?判断する方法】
他のグラフの傾きと比べてみる

注目点1:弟の歩きのグラフ(8分から12分の間の黒線のグラフ)
(2)の解答より、傾き90
注目点2:三輪車に乗っている時のグラフ(0分から8分までの黒線のグラフ)
8分で240m進んでいるので、240÷8=30
よって傾き30
多分正しい?をグラフを見ながら判断してみましょう。
傾き-54、切片が816でした。特に切片の数値は「間違った?」って思っちゃいますよね。
◎符号が「-」。グラフも右下がり。
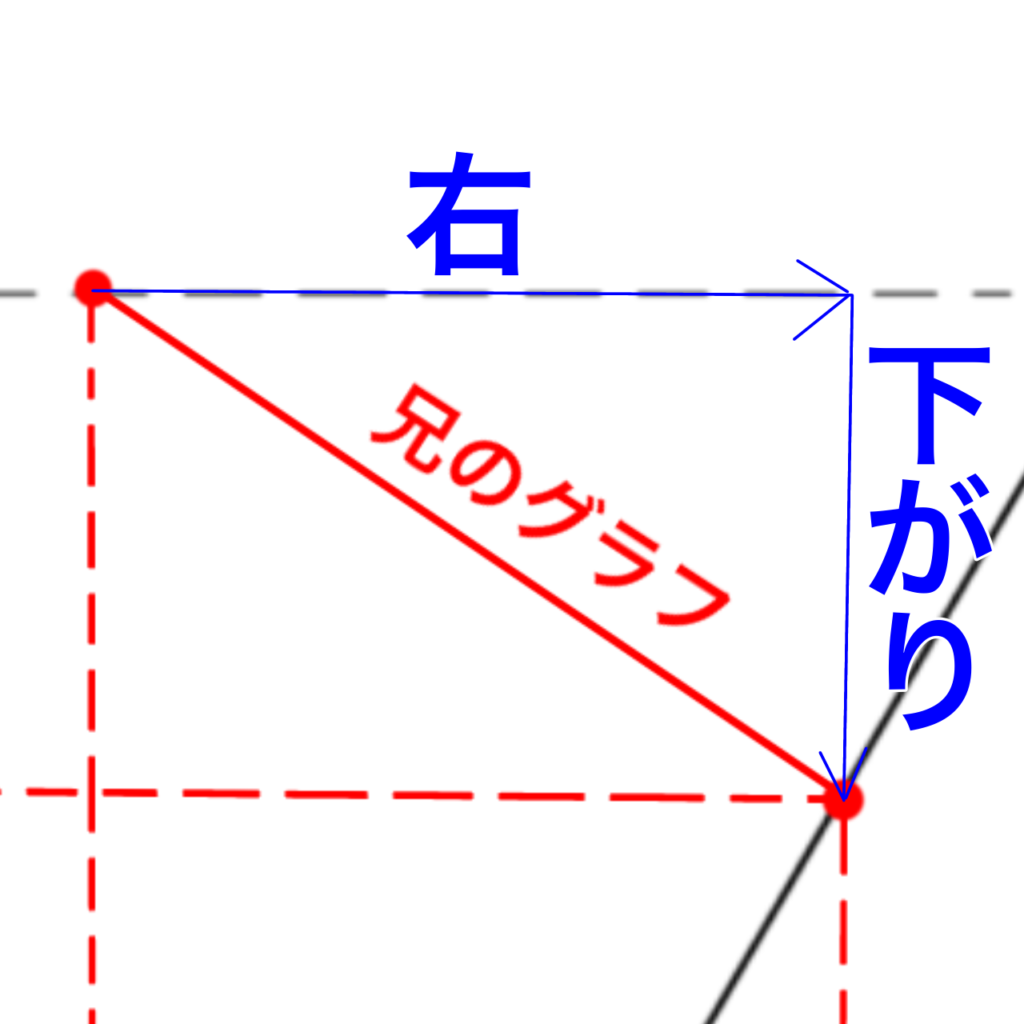
とりあえず間違いありません。
◎傾きの数値を他のグラフと比較してみるとだいたいそれっぽい。
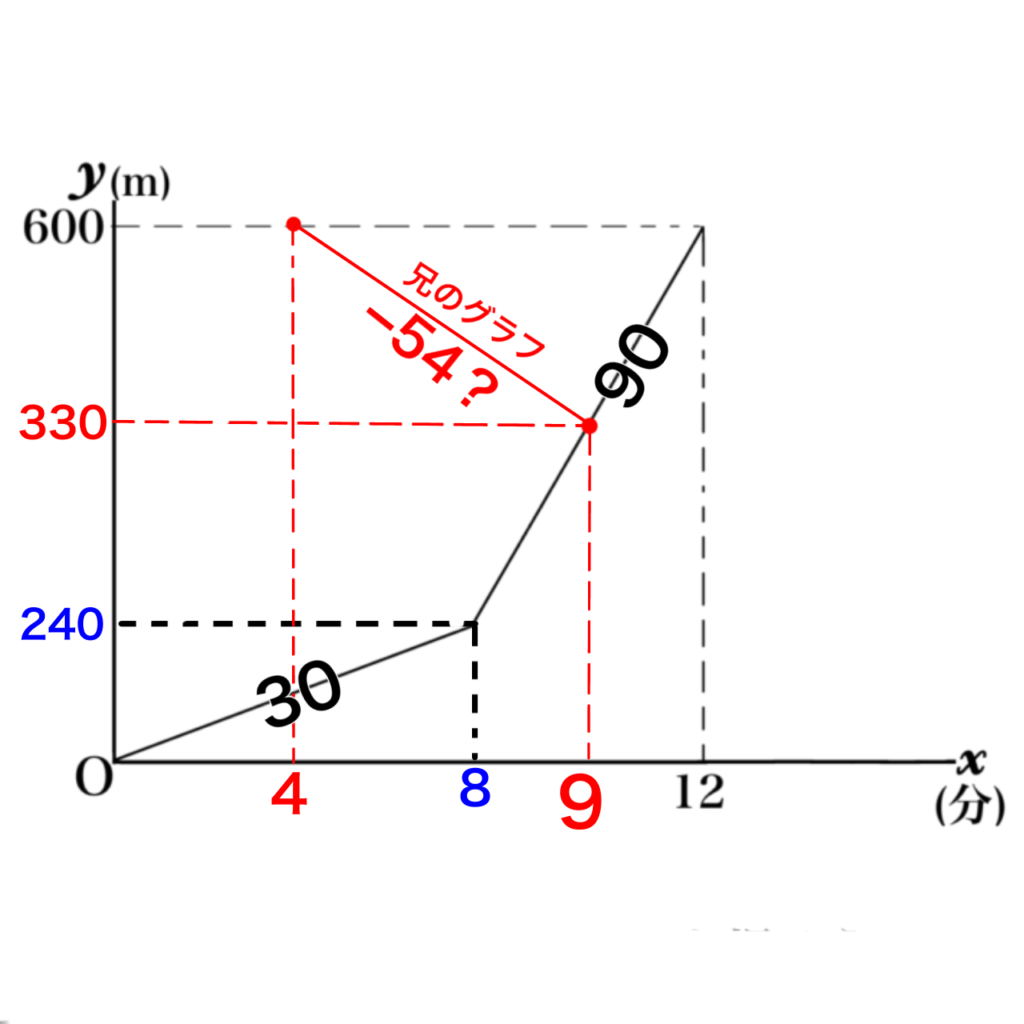

上がるか下がるかの違いはあるけれど、
30よりは傾斜が急だし
90よりはゆるやか。
だいたい54っぽくね?

な~るほど。っぽいね!
【切片が正しいかどうかを判断する方法】
グラフを延長して\(y\)軸のどの辺に来るかを確認する
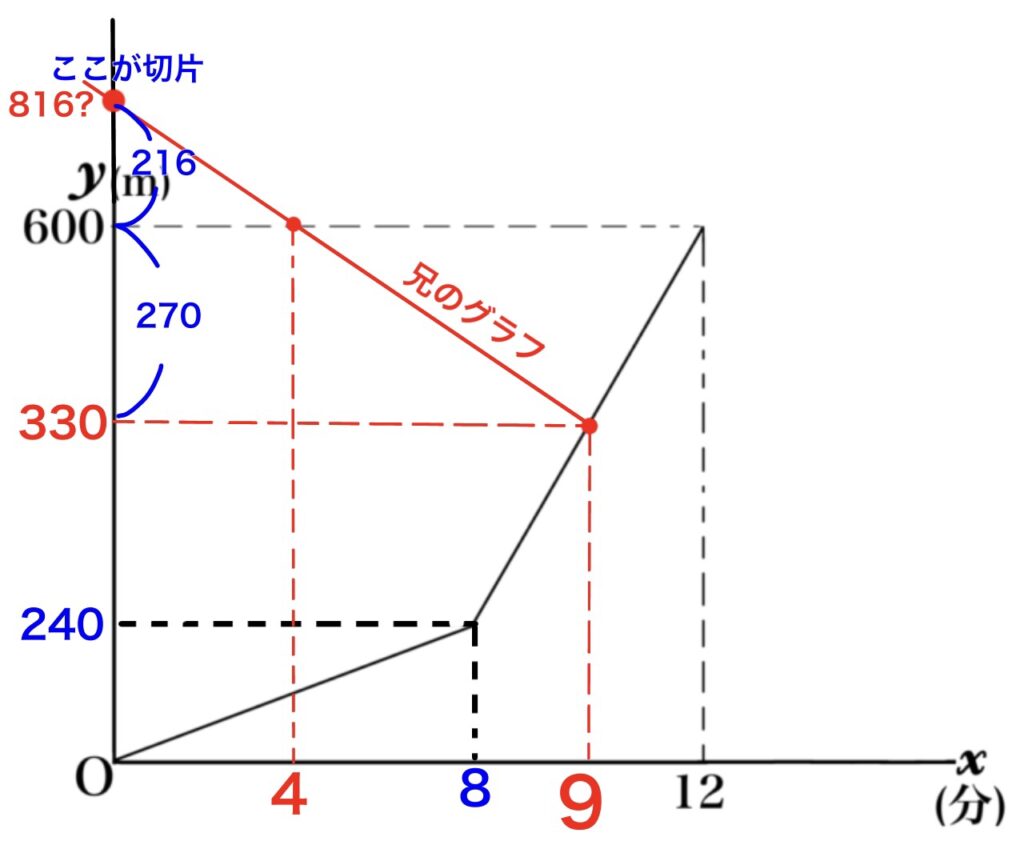

こうやってみるとだいたい合ってるっぽいよね?

それっぽいです!
こうやって「だいたい合っている」ことを確認します。
グラフ的にだいたい合っていて、計算が間違いなければ、「答えは間違っていないだろう」と推測できますので、その場合は自信を持って答えを書いてください!
(4)の解き方 解答・解説

グラフを見て考えましょう。弟が三輪車に乗っているのは8分後までです。
つまり、下の図のココまでには弟に会わなければいけません↓
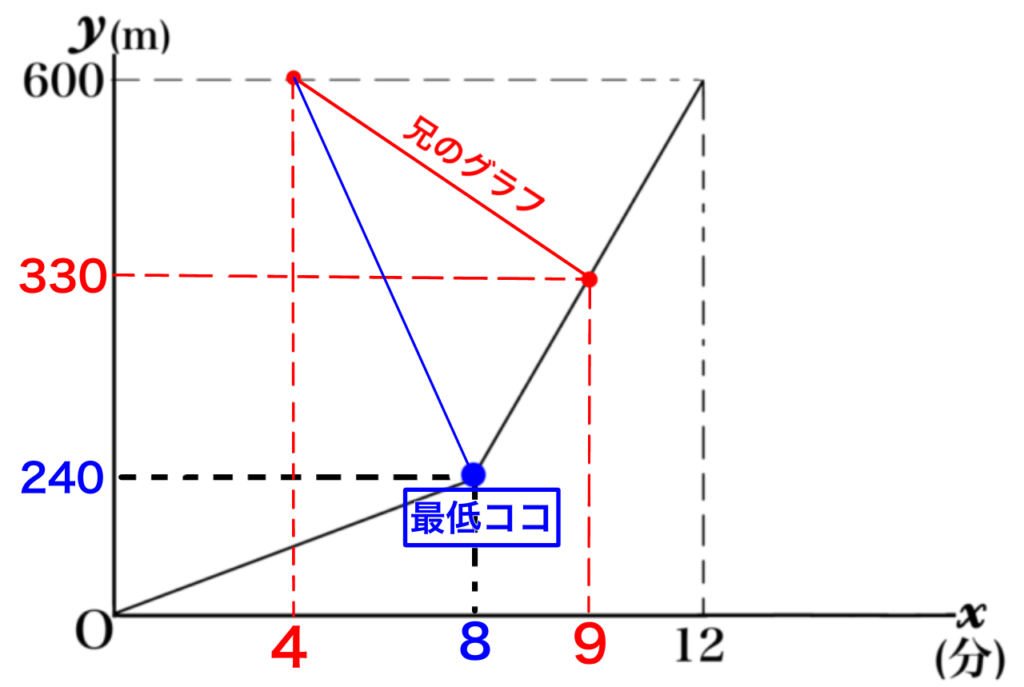
(4,600)(8,240)この2点を通る直線の傾き(=速さ)で進むのが最低条件です。
この2点の傾きを求めましょう。
\(\dfrac{600-240}{4-8}=\dfrac{360}{-4}=-90\)
最低必要な速さ 傾き-90⇒分速90m
(3)の解答より、兄のグラフの傾き-54⇒分速54m
最低でも何倍の速度で進むべきだったか?
90÷54=\(\dfrac{90}{54}=\dfrac{5}{3}\)
よって、\(\dfrac{5}{3}\)倍以上
これで完答です!
今回は直線の式の求め方を連立方程式を中心に解説しましたが、他の方法でも当然問題なくできますので、好みの方法で解いてください。答えがあっていればOKです。
最後に

乗り捨てた三輪車は誰が回収したのでしょうか?

そこが問題?ウケる!!
数学の問題としては「そこが問題?」って感じですけど、
実際本当に乗り捨てていたら、現実社会ではそれこそが大問題ですよね。
基本があやしいな、と思う方はこちらをご覧下さい。
一次関数のこれまでの記事はこちらです⇩



楽しく覚えるならこちらもおすすめです!

コメント