和 差 積 商 とは
和⇒たし算
差⇒ひき算
積⇒かけ算
商⇒わり算
例
\(x\) と \(y\) の和は?⇒\(x+y\)
\(x\) と \(y\) の差は?⇒\(x-y\)
\(x\) と \(y\) の積は?⇒\(x\times y\)⇒\(xy\)
\(x\) と \(y\) の商は?⇒\(x\div y\)⇒\(\dfrac{x}{y}\)
大なり 小なり とは
不等号「>」⇒大なり
不等号「<」⇒小なり
不等号「≧」⇒大なりイコール
不等号「≦」⇒小なりイコール
…と言ったりします。私はあまり使いませんけど。
例
\(x\) 大なり5⇒ \(x >5\) (\(x\)は5より大きい)
\(x\) 小なり5⇒ \(x <5\) (\(x\)は5より小さい・5未満)
\(x\) 大なりイコール5⇒ \(x\geqq 5\) (\(x\)は5以上)
\(x\) 小なりイコール5⇒ \(x\leqq 5\) (\(x\)は5以下)
「以上」・「以下」はその数を含みます。
\(x\geqq 5\)⇒\(x>5\) か \(x=5\)
5でもOKだし、それより大きくてもOK。
「より大きい」「より小さい」「未満」はその数を含みません。
\(x <5\) ⇒5ではダメ。5より小さければOK。
(「4.999999………9」でも5より小さいからOK。)
絶対値とは
「0からの距離」を意味します。
例:絶対値3
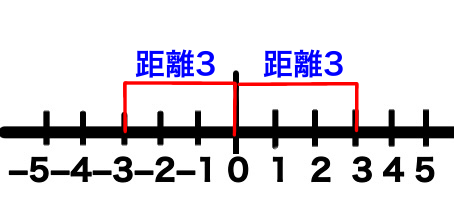
上の図のように、+3も-3も0からの距離は3なので、
どっちも「絶対値3」です。だから、
絶対値3の答えは、3と-3です。
こんな問題もあります。
問題 -5の絶対値を求めよ。
考え方は同じです。-5は、0から5個はなれているので、距離は5。
つまり、絶対値5です。
絶対値は、-でも+でも「数字の前の符号がない(+になる)数」と考えれば良いでしょう。
変域とは
「どこからどこまでの範囲か」ということです。不等号(<,>,≦,≧)を使って表します。
例題:10個のリンゴがあります。何個まで食べられますか。食べる個数を \(x\) として変域で表しなさい。

私は1個で十分です。

私は3個食べちゃう!

10個食べてもいいの?ならフツー10個挑戦するでしょ!
と、人によって様々ですね。もしかしたら1個も食べたくない人もいるかもしれません。つまりこの場合、食べる数は人によって0個から10個まですべて可能性があります。それを不等号を使って表すのが変域です。
\(0\leqq x\leqq 10\)
このように、間に「 \(x\) (ここでは食べる個数)」 をはさんで、どこからどこまで変化する可能性があるかを表します。これが変域です。
注意点!
間違い例1(今の例題の場合でのよくある間違い)
\(x\leqq 10\)
これだと、\(x\)は10以下ならOKになっちゃって、マイナスの数でもOKということになっちゃいます。つまり「-1個食べる」が可能ということです。

-1個食べる…
1個吐きだ…

はい!その想像はやめよう!
間違い例2(今の例題の場合でのよくある間違い)
\(0<x<10\)
不等号の下に「=」がないと、0や10は含まないことになります。つまり「食べない」という選択、「全部食べる」という選択ができなくなっちゃいます。

でも1度に10個なんて食べませんよね。普通。

だよね!私やっぱ3個無理かも。
\(1\leqq x<3\)くらいかな。

2.9はアリなんか~い!!
そこまで行ったら3個全部食え!ww
「自分なら…」とか「実際…」などの考えではなく、可能性があること全部を表しましょう!フードファイターの方なら10個くらい楽勝かもしれませんしね。
弦とは 弧とは
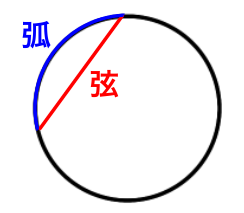
弦⇒円周の2点の間をつないだまっすぐな線
弧⇒円周の一部分
イメージとしては弓ですかね。

矢をつがえて引っ張る方を「弦」、弦を張ったときに曲がる方が「弧」って感じです。
母線とは?
円を…
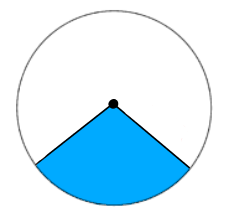
ケーキを切るように、中心からのばした線(半径)で切った青い部分がおうぎ形です。
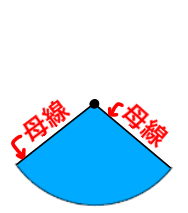
おうぎ形の線で、切る前は元々半径だった線を母線と言います。

おうぎ形の母線同士をくっつけて丸めると円錐ができますが、円錐の頂点から底面につながる図のラインも、元々の円の半径と同じ長さなのでこれも「母線」と言います。
係数とは?
文字に付いている数字のことです。厳密に言えば、文字とかけ算でつながっている数字が係数です
\(3x\)
\(x\) に付いている3が係数です。
\(4x^2-\dfrac{1}{2}x-1\)
\(x^2\)に付いている4が\(x^2\) の係数です。
\(x\)に付いている\(-\dfrac{1}{2}\) が\(x\) の係数です。
文字の付いていない\(-1\) は係数とは言わず「定数」と言います。次の項目「定数とは?」をご覧下さい。
定数とは?
「定まった数」ということなので、一般的には「文字が付いていない普通の数字(分数や小数なども含む)」を定数と言います。
文字は普通、その時によって1になったり2になったり色々な値をとります。
そうすると例えば\(3x\) は、
\(x=1\) のとき3になり、\(x=2\) のときなら6になります。このように場合によって値が変わっていく数を「変数」と言いますが、逆に定数は1つの値に固定された数です。
「変数」じゃない数が「定数」ということです。
つまり、\(3\) とか\(-5\) とか\(-\dfrac{1}{2}\) なども、値が定まっているので「定数」になります。

え?だって\(3\) とか\(-5\) は整数じゃないの?
\(-\dfrac{1}{2}\) だって分数だよね?

「定数」というのは「変数」に対して使われる言葉じゃ。
「値が変わらない数だよ」という意味で言われるのじゃ。

それぞれ名前はあるけれど、「動物」に対して「人間」
「男」に対して「女」という違う区分けがあるということですね!

お!今日は冴えておるのぅ。そういうことじゃな。

「今日は」は余計です!

なーるほど!
とにかく、値が変化しない数を定数と呼ぶわけです。
補足
例えば「1つに決まっている数なんだけど、今は分からないから\(m\) に置いておく」のような場合だと、この\(m\) は「定数」になります。
次数とは?
\(3a\) のように、「×(かける)」を省略して1つのまとまりになったものを「項」と言いますが、項にある文字の数が「次数」です。
\(3a\)⇐\(a\)という文字が1つあるから「次数1」
\(2xy\)⇐\(x\)と\(y\)で2つ文字があるから「次数2」
\(4x^3\)⇐\(x^3\)は、\(x\)が3個を意味するので「次数3」
ちなみに、\(-5\) は、文字が1つもないので「次数0」です。
+やーで繋がれた式(多項式)の場合
一番多い次数が代表になって、式全体の次数を決めます。
\(2x^2-3x+1\)
この場合は、\(2x^2\)が次数2、\(-3x\)が次数1、\(+1\)が次数0なので、
次数が一番多いのは「2」です。なので、式全体は「次数2」となります。
補足
「次数2」の式のことを「2次式」と呼びます。
「次数3」の式なら「3次式」となります。
くくる とは?
式を共通の数や文字を使って( )でまとめることを言います。これは中3で出てくる因数分解の一種です。
例:\(2x+8\)
各項\(2x\) も\(8\) も2の倍数です。つまり2が共通しているので、2を外に出してまとめることができます。
\(2x+8=2\left( x+4\right)\)
これが「くくる」という作業になります。
( )内に2をかけると元に戻ります。
「くくる」のイメージ画(画力は仕様ですw)

ただ普通に流している髪。

これを元の状態
\(2x+8\)
とします。

ゴムでくくった髪。

「2」というゴムで髪をまとめました。

ほどけば元に戻ります。

アイちゃん、くくってる~!

あ!あたしのことだわ!
こんにちは。「くくる」です。

ほどくと何倍になるんですか?

作者の画力次第!

それなら絶対くくったままだよ~。
作者、画力ないもんww

うるさいでおじゃる!
補足
2でくくった場合、( )内は元の数を2で割った数が入ります。
\(2x+8\)
\(=2\)\(\left( x+4\right)\) ⇐2で割った数
3でくくったら、( )内は元の数を3で割った数が入ります。
\(6x-9\)
\(=3\)\(\left( 2x-3\right)\) ⇐3で割った数
展開 とは?
「くくる」の逆です。(「くくる」を押すと項目にジャンプします)
\(2x+8=2\left( x+4\right)\)
これが「くくる」でしたが、
\(2\left( x+4\right)=2x+8\)
このように、分配法則を使って( )をはずすことを「展開」と言います。
\(\left( x+3\right)\left( x-5\right)\)
\(=x^2-5x+3x-15\)
\(=x^2-2x+15\)
このようにかけ算をして( )をはずすのも分配法則なので「展開」と言います。
補足
展開⇔因数分解
因数分解されてあるものを計算して( )をはずすのが「展開」
展開されてあるものを( )でまとめるのが因数分解。
2つは逆の性質を持つ言葉だと理解しておきましょう。
平方 とは?
2乗のことを「平方」と言います。
5²(5の2乗)は「5の平方」とも言えます。
よく文章問題で、
「\(x\) に2加えた数の平方は」
みたいな出題の仕方を見ますが、これの意味は
「\(x\) に2加えた数の2乗」と同じ意味です。
つまり、\(\left( x+2\right)^2\) ということですね。
補足
聞き慣れない言葉のように感じますが、実は小学校のときから使っている言葉なんです。
面積の単位「cm²」これを「平方センチメートル」と読みますよね?
「cmの2乗」と書いて「平方センチメートル」。
平方=2乗
分かれば難しい言葉ではありません。
数学の文字 x y n P Q r ‘(ダッシュ)
x とは? xの書き方は?
わからない数、不明な数、求めたい数を文字で表すときの代表です。
なぜ\(x\) になったかは諸説あるようですが、とりあえずわからない数は\(x\) にしておけばよい、って感じです。
xの書き方
一画目が赤、二画目を青で示しました。
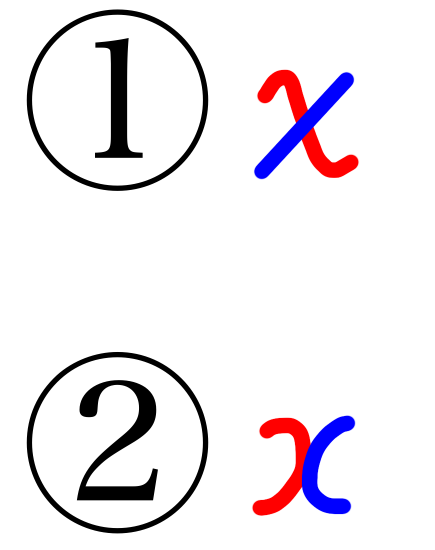
一般的にこの2つの書き方があります。個人的にはどっちでもいいと思います。
ただ、様々なご意見を伺うと、①はギリシャ文字の「χ(カイ)」と同じになるから、②の書き方の方がいいとおっしゃる方が多い気がします。
ちなみに私は、小学校~中1くらいまでは②の書き方で、中2~大学くらいまでは①の書き方でした。今は②で書いています。
現在②で書いている理由は、小学校では算数で\(x\) が出てくるときに②の書き方で教わるようなので、それに合わせて②で書いています。中学生や高校生はどっちで書いても受け入れてくれますが、文字自体が初めての小学生は混乱する可能性があると思うからです。人によって使い分けるのも面倒なので小学生に基準を合わせています。
でも、数学の文字は筆記体で表されているので、そういう意味では①の方が正しい気もします。だから私は見分けがつけばどっちでも良いと思います。
y とは? なぜ y なのか y の書き方
2つ目のわからない数、不明な数、求めたい数を文字で表すときの文字です。
\(x\) がすでに使われているとき、もう1つわからない数があるときに\(y\) を使うのが一般的です。
なぜ\(y\) なのか?
単にアルファベット順で\(x\) の次が\(y\) だからです。
\(x\) の次にわからない数は\(y\) 。それだけの話です。
y の書き方
\(y\)
筆記体でこんな感じで書きます。
でも、みんなが\(y\) だと判断できる書き方であれば、多少違っても問題ないと思います。
n とは?
通常、分数や小数ではなく「ここには整数が入るよ」というときに使う文字として使用されます。
「number(数)」の頭文字です。
ちなみに、2つ目の整数の場合は\(m\) を使います。

さっきの\(x\) と\(y\) の規則だとアルファベット順でしたよね?
\(m\) はアルファベット順で\(n\) 前ですよ?

\(n\) の次は\(o\) じゃろ?
\(o\) だと「0(ゼロ)」と間違えやすいから\(n\) 近辺の文字ということで\(m\) になったそうじゃ。

意外とテキトーだね
P とは? Q とは?
座標や動点などの1つの点を文字で表すときにPを使います。
英単語「point(点)」の頭文字です。

アルファベット順でPの次がQだから2点目はQなんだね?

その通りでおじゃる。

でも座標はAやBで表す場合も多いですよ。

A、Bの方が感覚的にしっくりくるからでおじゃろ?
「絶対Pじゃないとダメ」というわけではないでおじゃる。
r とは?
中学では「半径」を表すときに出てきます。
英単語「radius(半径)」の頭文字です。
’(ダッシュ)とは?
1つの点を動かしたあとの点や1つの式を変形しただけのものを表すときに使ったりします。
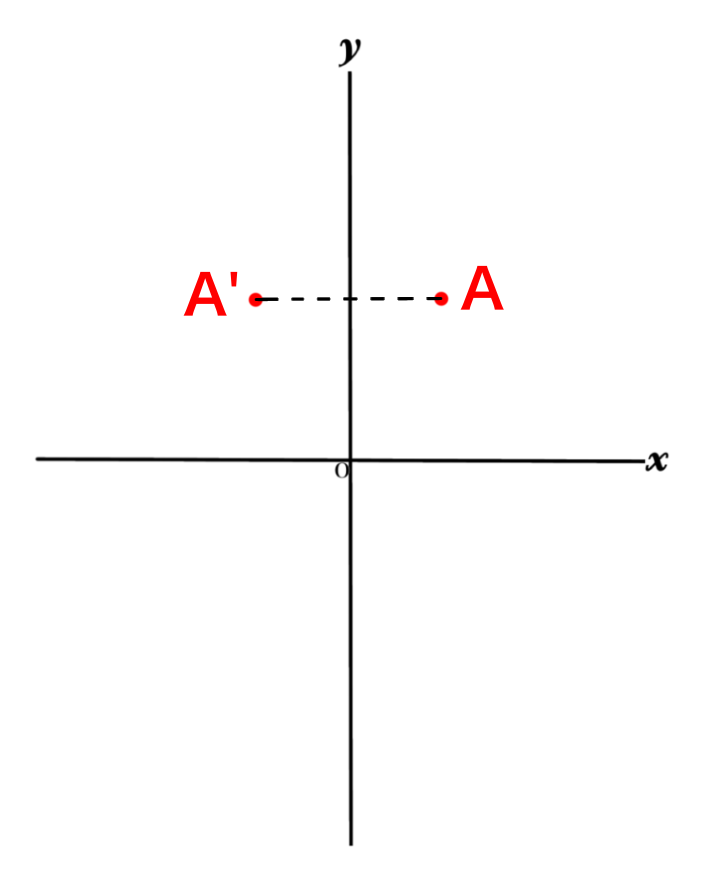
点Aを\(y\) 軸対称に移動した点を
「A’」としたりします。
もちろん、Bなどに置かれる場合もありますけどね。
\(2x+y=1\) …①
この式を\(y=\) の式に変形すると
\(y=1-2x\) …①’
こんな感じで使ったりもします。
元々のものを何かの法則で変化させた場合に使うことが多いです。


あ、変形した!
だからダッシュ?

ちなみに「妾」は自分のことをへりくだって言う昔の言葉ですね。
普通女性が使うはずですが…。

雰囲気じゃ!雰囲気!!

わーい!テキトー!!
数学の文字まとめ
どの文字がどういう場面で使われるのか、というのは「昔からの習慣」として伝わってきているものが多いです。決まった文字を使った方が図を見たときにみんな共通で意味を理解できるようにするためだと思います。
でも、「絶対こうじゃなきゃダメ!」というものではありません。ある程度は覚えておいた方が良いとは思いますが、「よくこの文字で置かれているなぁ」程度の認識でOKです。
何を示しているのかが分からなくならないように配慮する。
それが一番大切だと思います。
そうじゃないと自分で文字に置いたものが、何が何だか分からなくなって、自分自身が混乱するということにもなりかねませんから。


コメント