まずは基本の規則
同符号同士のかけ算、割り算
⊕×⊕=⊕ ⊕÷⊕=⊕
⊖×⊖=⊕ ⊖÷⊖=⊕

異符号同士のかけ算、割り算
⊕×⊝=⊖ ⊕÷⊝=⊖
⊖×⊕=⊖ ⊖×⊕=⊖

乗法(かけ算)と除法(わり算)の符号の決まりはこれだけです。あとは符号を間違えずにかけ算、割り算をするだけです。
累乗の基本事項
3² ⇒ 3を2回かけて下さいという意味(3×3=9)
5³ ⇒ 5を3回かけて下さいという意味(5×5×5=125)
累乗の注意点
数字の上に付いている□²や□³のような小さい数を「指数」と言いますが、指数は基本的に直前のものにしか効果はありません。ですので、
ー3² の2乗は、すぐ直前の3にしか効果がありません。
つまり、
ー3²=ー3×3=ー9 となります。
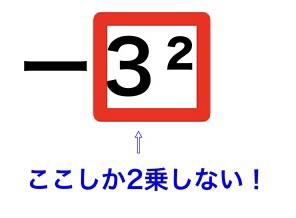
しかし、
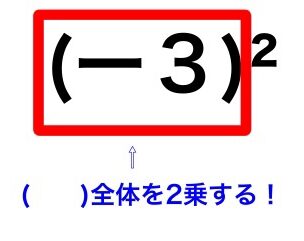
(ー3)² ⇐このように( )の外に指数が書かれた場合は、( )の中全体を累乗します。
つまり、
(ー3)²=(ー3)×(ー3)=9 こうなります。
人を惑わすようなこんな問題もあります。
(ー3²) ⇐( )はあるけれど、2乗が中に入っています。
この場合は、( )がない時の計算と同じです。直前の3にしか累乗の効果は及びません。
(ー3²)=ー3×3=ー9 こうなるということですね。
この注意点の他のよくあるミスを挙げていきます。
よくある累乗の計算ミス
① 3²=6 としてしまう
3²は、3を2回かけるから…3×2 としてしまうミスです。
これは多少慣れた人でもやってしまいがちなミスなので注意しましょう。
正しくは、3²は、3を3を2回かけるから…3×3=9 です。
②1²、1³
「同じ数を2回かけるんだ」と分かっていても、1²=2⇐間違い 正解は1²=1×1=1
「同じ数を3回かけるんだ」とわかっていても、1³=3⇐間違い 正解は1³=1×1×1=1
なぜか、1のときに累乗の間違いをする人は多いです。気持ちは分かりますけど注意しましょう。
3つ以上の数のかけ算とわり算
(ー2)×(ー5)×3
(ー4)÷(ー3)×(ー6)²
このような計算の手順を紹介します。
計算の手順
(ー4)÷(ー3)×(ー6)² この計算を例に説明していきます。
まずは式を書きます。
1,累乗がある場合は累乗の計算をする (図1)
2,計算結果の符号を決めてしまう(図2)
3,「÷の後ろは分母、それ以外は分子」として、式を分数にする。(動画1)
4,約分がある場合は約分をして答えを出す。(動画1)
5,最後に符号を間違っていないか確認する。(動画1)
(ー4)÷(ー3)×(ー6)²
図1⇩

図2⇩
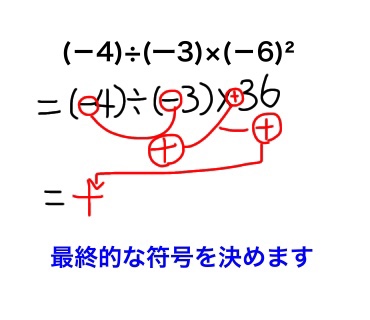
動画1⇩
このような手順で進めれば、ミスも確実に減ります。
3つ以上の数のかけ算、割り算で注意しておきたいことは、次の2点です。
①符号のミス
②かけ算、割り算の順番のミス
①の「符号のミス」には充分注意をすることが大切になります。先程の手順にも書いてあったように最後にも符号が合っているかどうかを確認しましょう。
②のかけ算・割り算の順番について説明をします、
例題 6 ÷ 3 × 2
この計算を3 × 2から計算すると間違います。
6 ÷ 3 × 2 = 6 ÷ 6 = 1 ☜間違い
6 ÷ 3 × 2 = 2 × 2 = 4 ☜正解
「かける」と「わる」って同じ順番だから、どっちから計算してもいいんじゃない?
そう思う人もいると思います。さて、それではなぜ上のような間違いになってしまうのでしょうか?
下の動画をご覧ください。
やり方としては⇩の方が簡単です。
さて、それではこの辺に注意をして問題をやってみましょう。
この単元の練習問題を作成しました。
もし良かったら下の問題をやってみてください。
問題
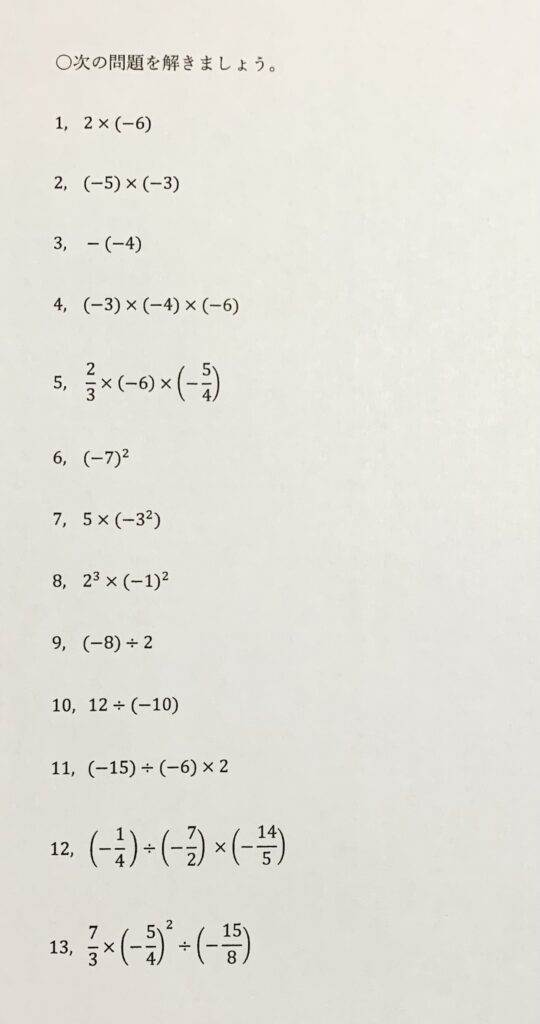
下に解答解説動画がありますので、参考にしてみて下さい。
解答と解説動画
解答解説動画
動画を見る暇がない人などは、以下に解答を貼っておきますので確認してみて下さい。
この後は、なぜ同符号同士の×÷が+になって、異符号同士の×÷が-になるのかを説明します。
興味があればご覧ください。
⊕×⊖=⊖ ⊖×⊖=⊕ になるのはどうして?
500円もらうことを「+500」とすれば、
500円あげることは「ー500」となります。
機会(チャンス)が2回あることを「+2」とすれば、
機会(チャンス)が2回失われることは「ー2」となります。
図3の左側を「自分」として見て下さい。
500円もらう機会が2回あれば、1000円得をします。
+500×(+2)=+1000円
500円もらう機会が2回失われれば、1000円損をします。
+500×(ー2)=ー1000円
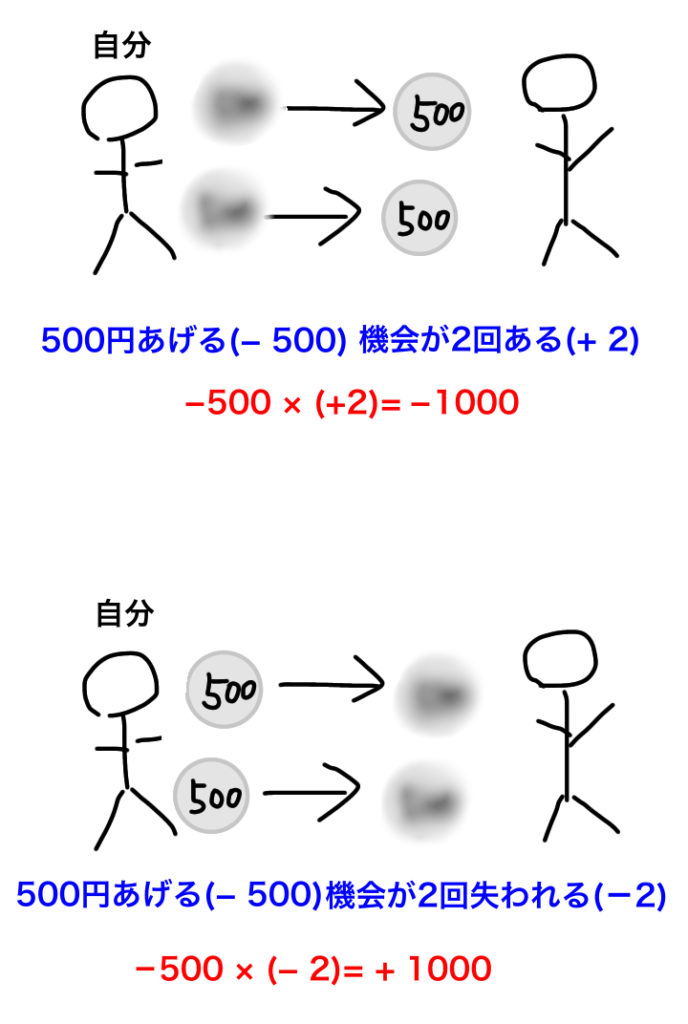
500円あげる機会が2回あれば、1000円損をします。
ー500×(+2)=ー1000円
500円あげる機会が2回失われれば、1000円得をします。
ー500×(ー2)=+1000円
図3
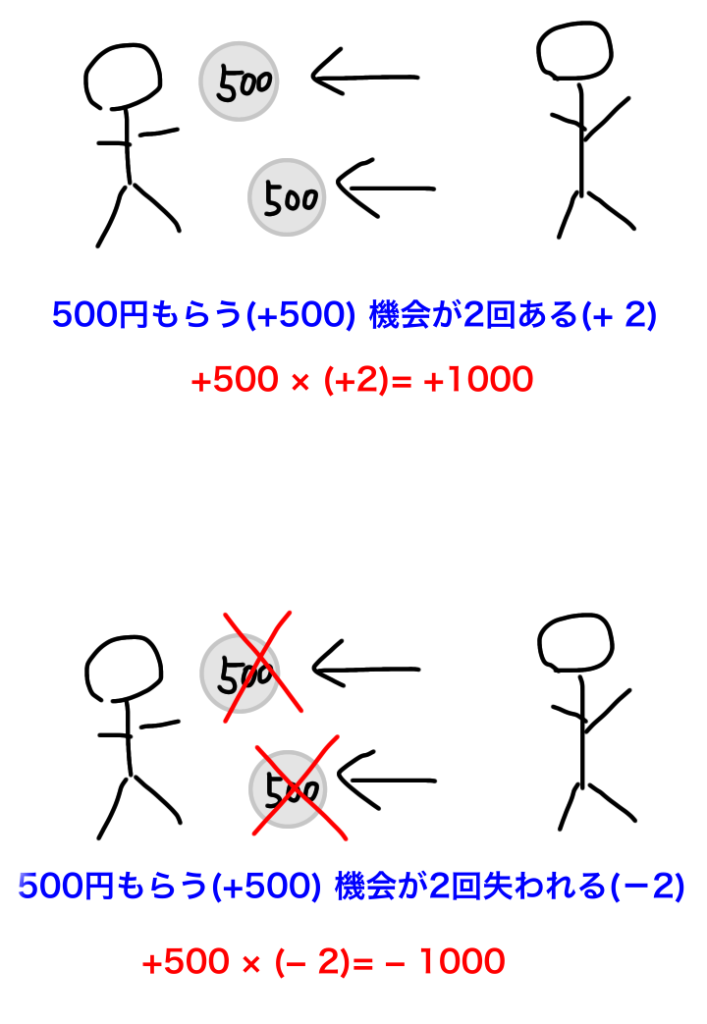
図4
このような例で考えると分かりやすいかな?と思い提案してみました。
数学はただ単に公式で覚えるよりも、イメージで覚えた方が理解しやすいです。
どのようなイメージで計算が成り立っているのかを教える人は伝え、習う人は覚えるのが一番です。
しかし、深堀りして覚えることを望んでいない人に、教える側だけが一生懸命伝えようとしても効果は薄いです。「なぜこうなるんだろう?」という疑問が沸き上がってきた時にすかさず教えられるように、教える側の人は準備しておきたいですね。


コメント