この動画を見て納得できればOK!
まずは解き方を確認してみましょう。
この動画を見て「そうやるのか!」と思えればOK!あとは問題練習してみましょう。
納得できましたか?
見ても「なんで?」と思うときは、下の解説をご覧ください!
代入法の混乱ポイント
※上の動画とは違う例題です。下の式を使って説明します⇩
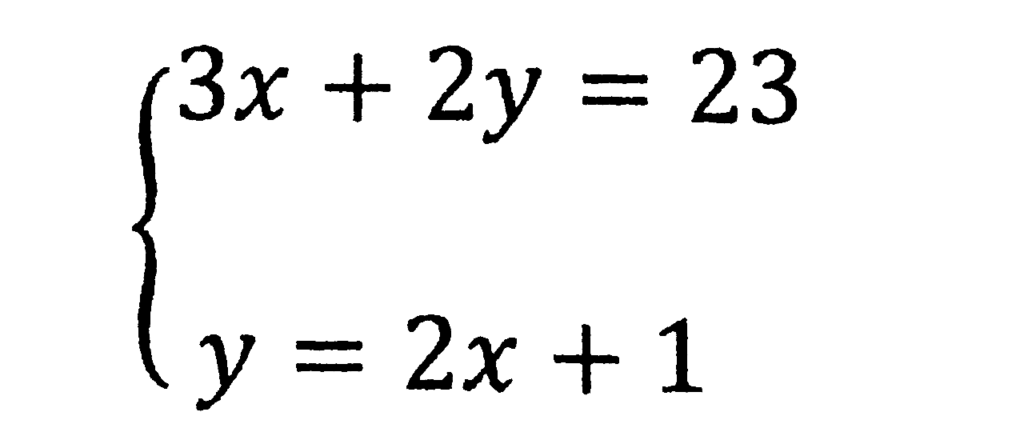
連立方程式で代入法の式を見たときや、解き方の説明を聞いたときの違和感。
「yのところに2x+1を代入って…なにごと?」
そう思った人、けっこういるんじゃないでしょうか。
代入法で引っかかる人の多くが思うこと。
「何が同じなの?」
「なんでこれが入るの?」
「yの代わりに入れるって何?」
このような疑問だと思います。
でも、こういう式だったらどうでしょう?
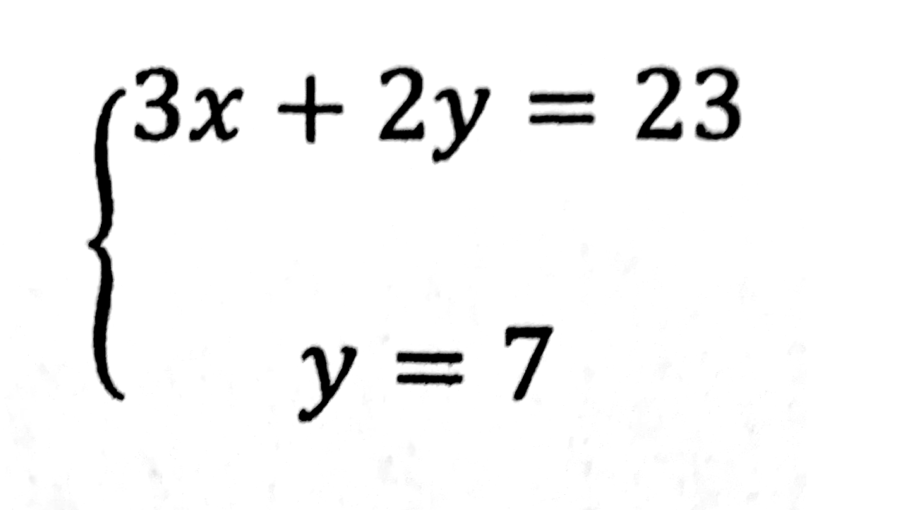
式の書き方に違和感はあるかもしれませんが、
「y=7だから、yに7を入れればいいのかな?」
と、思えるんじゃないでしょうか。
でも、y=2x+1のようになっていると、y は「数字の代わりに入っているもの」と理解しているので、
「2x+1って数字じゃなくて『式』じゃん!」
と、感じてしまうのだと思います。これが混乱のポイントです。
この混乱をなくすための説明をしたいと思います。
ひとまとまりの数
y=(普通の数字)の場合
先程の例で説明します。
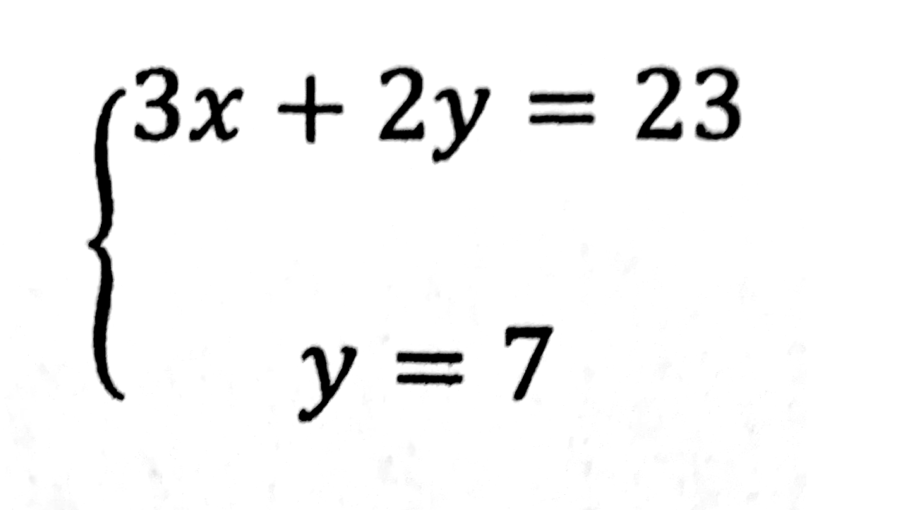
これであれば、上の式の y に7を入れて解けばいいので、下のようになります⇩(解き方解説動画も参照してください)
3x+2×7=23
3x+14=23
3x=23-14
3x=9
x=3
このように計算できます。
これは、連立方程式の加減法でも同じような計算が出てくるので、加減法をクリアした人ならば問題なくできるでしょう。
「1つの数」と考えること
全部が数字の場合
しかし、これが先程の例
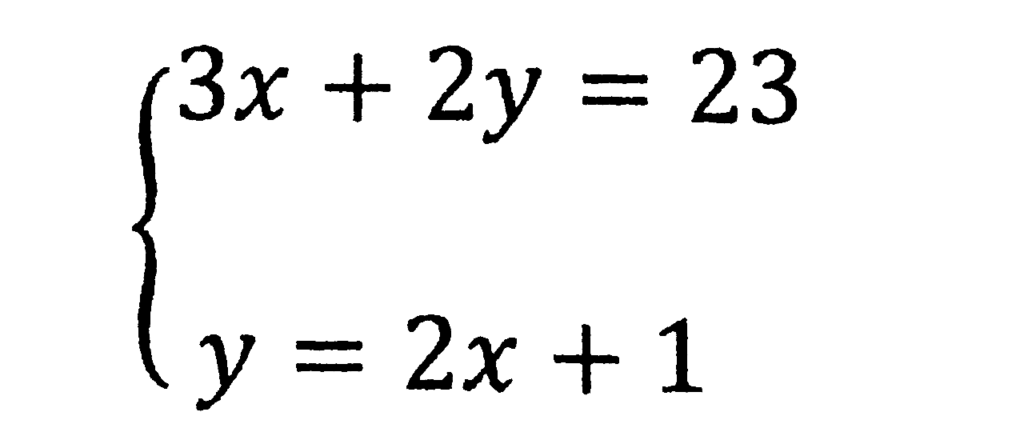
このようになると
「…?」
となる人が多いです。
ここで重要な考え方!
2x+1を、1つの数と考えること!
「数?え~?式じゃん」そう思う人も多いでしょう。
それじゃあ例えば、
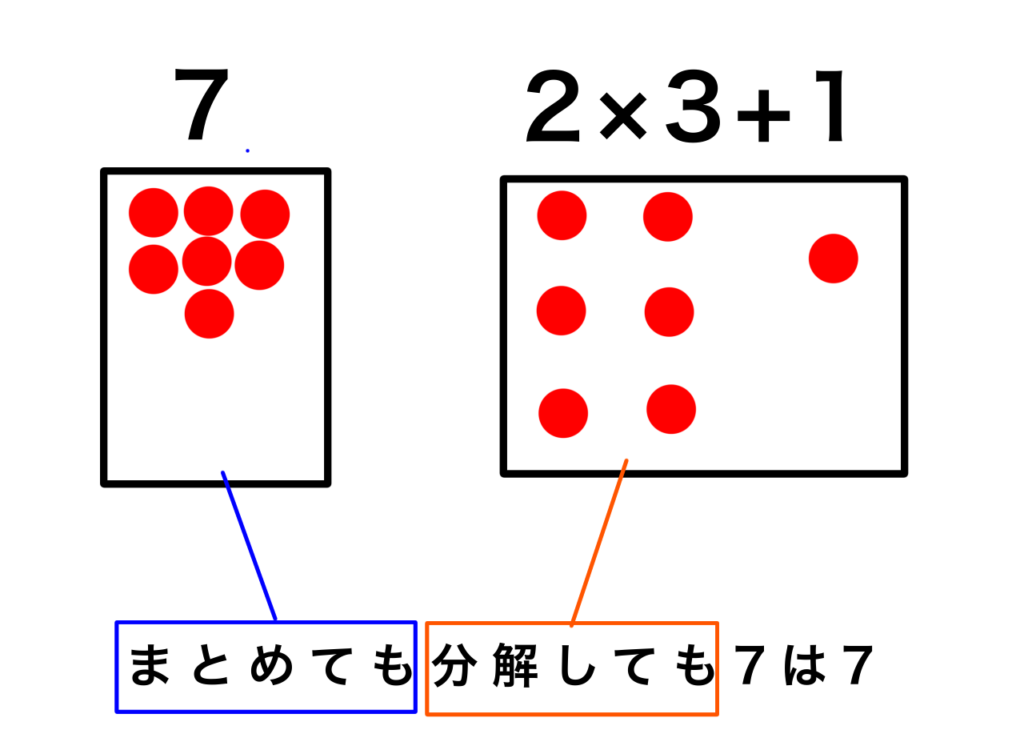
y= 7
y= 2 × 3+1
この2つを見比べてみてどう思いますか?
形は違うけれど結局計算すれば何も変わらないですよね?
それではこれを代入するとどうなるでしょう?
y に 2 × 3+ 1を代入します。でもこの数は7を分解しただけで、元々「1つの数」なので、これを( )でくくって、y=(2×3+1)として計算します。
3x+2 × (2 × 3 +1)= 20
↑(結局カッコ内を計算すると7)
3x+2×7 = 20(こうなります)
2x+14 =20
2x=20-14
2x= 6
x= 3
当然、7 を代入したときと同じになりますよね。
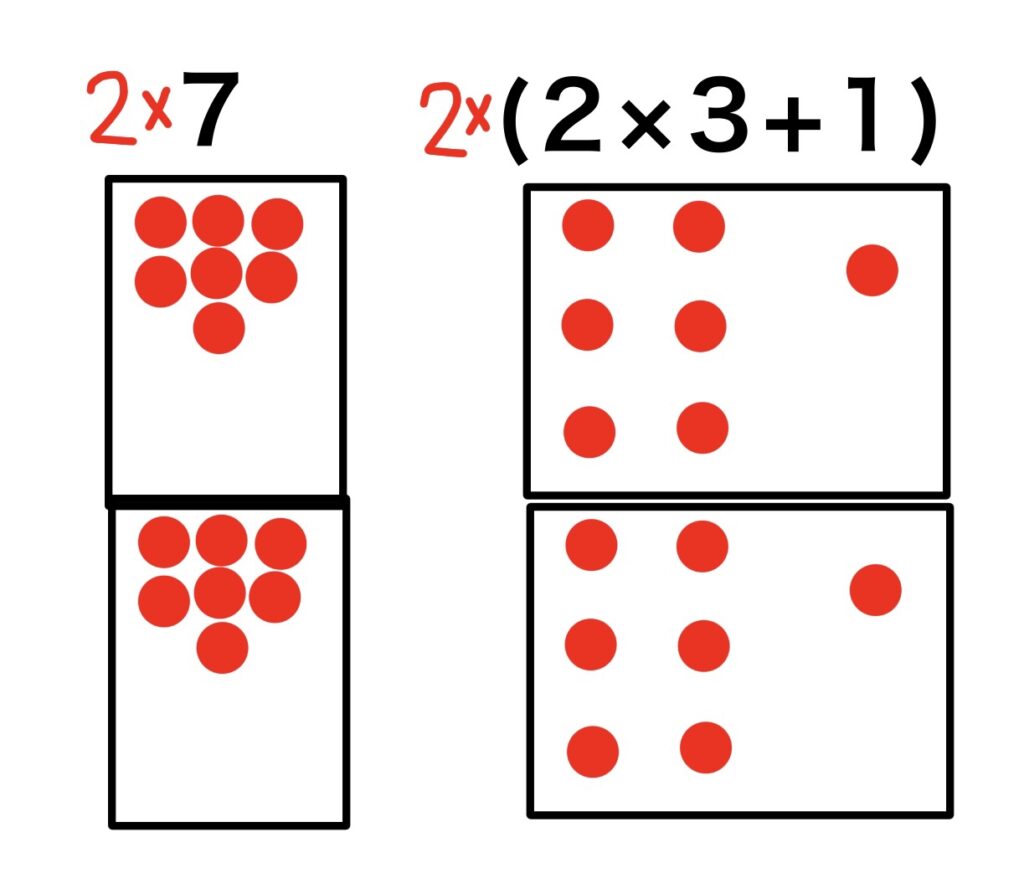
2倍しても数は同じ。
文字 x を使った場合
「2x+1」のような「数」は、x がいくつなのか分かっていないだけで、もし x がいくつなのか決まれば「1つの数」になります。
x=1のときは2×1+1=2+1=3
x=2のときは2×2+1=4+1=5
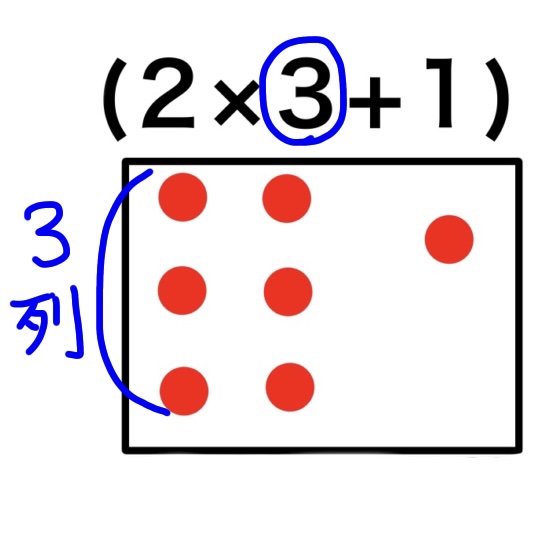
図Aでは x=3 なので
x=3 のときは2×3+1=6+1=7
になっています。
図 A ⇩
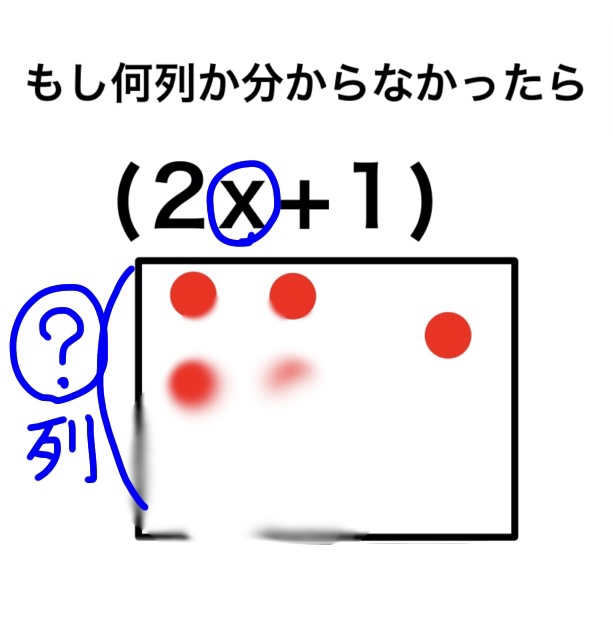
図Bは何列あるのか分かりません。だから、x の正体がまだ分からないので x のままにしておいて、「2x+1」としているだけです。
2×3+1の「3」が「 x 」に変わっただけの「1つの数」なのです。
(2x+1) と、カッコをつけて「1つの数である」ことを確認して、計算することになります。
「これで1つの数なんだ」という感覚を持てるようにしましょう。そうすると、代入法の考え方もスムーズにいくと思います。
図 B ⇩
実際に計算してみましょう
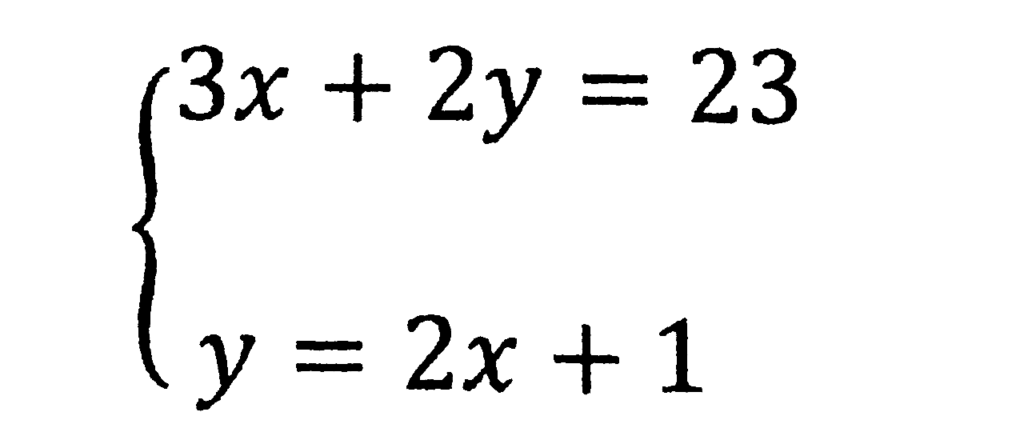
まずは、下の式y=2x+1にカッコをつけて、「1つの数」であることを確認します。
y=(2x+1)
そして上の式 3x+2y=23 の y のところに(2x+1)を入れます。
3x+2(2x+1)=23
計算していきます。
3x+4x+2=23
3x+4x=23-2
7x=21
x=3
下の式にx=3を代入
y=2×3+1
y=6+1
y=7
よって、x=3,y=7
この問題はこれで終了です。
連立方程式の代入法について、解き方、考え方が分かってもらえたら嬉しいです。
動画でもう一度確認しよう。
最後に、もう一度確認のために解説動画を用意しました。後半は一番最初に載せた動画と同じですが、前半に「数のまとまり」の説明を要約してあります。見て確認してみて下さい。


コメント