連立方程式とは
まず連立方程式っていうのは、数が分からないものが(下の式ではxとy)、1つの式に2つあります。
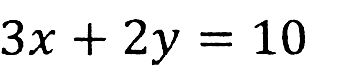
2つの分からない数があるままでは、解けるわけないんです。
それじゃあ2つの式を用意するので、それなら解けるよね?って問題なんです。
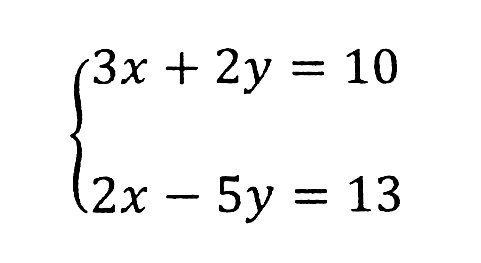
2つの式を使って、xかyかどっちかを消して計算しましょう!というのが連立方程式になります。
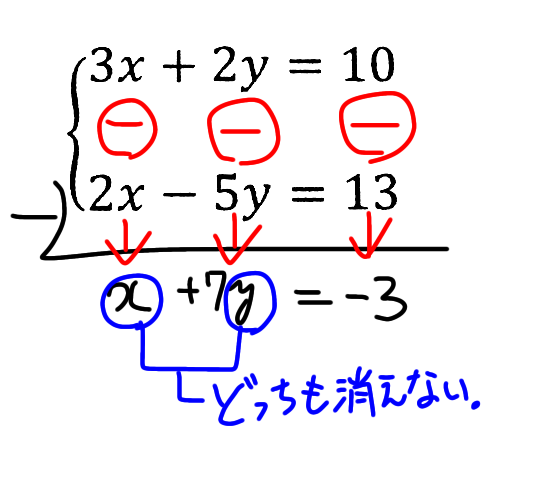
ただ、この式の場合はこのまま足し算や引き算をしても仕方ないです。
例えば足し算したら5x-3y= 23。

引き算してもx+7y=-3ってなるだけで、xもyもどっちも消えませんので答えが出ません。
じゃあどうすればいいか?
どっちかの文字が消えるように、式を何倍かしてやろうという方法を使います。
連立方程式の解き方のイメージ
それぞれの式を何倍かして数字を合わせ、それで足したり引いたりすることによって、xかyかのどっちかを消してやろうっていう考え方です。
手順
○xかyかの数字を合わせるために式全体を何倍かする
○数字を合わせたら足すか引くかして、xかyのどちらかを消す
手順的に言うと、まずはこの2つです。
xとyのどっちを消してもいいです。「こっちのほうが簡単かな」でもいいし「こっちの方を合わせたい」でもいいです。法則さえ間違っていなければどっちを消そうとしてもオッケーです。
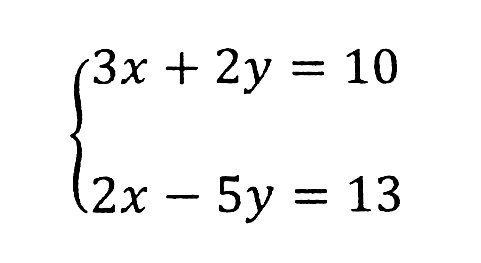
ここでは、xを消すために、xが付いている数字を合わせるとしましょう。xの方の数字は3と2なので、最小公倍数は6です。
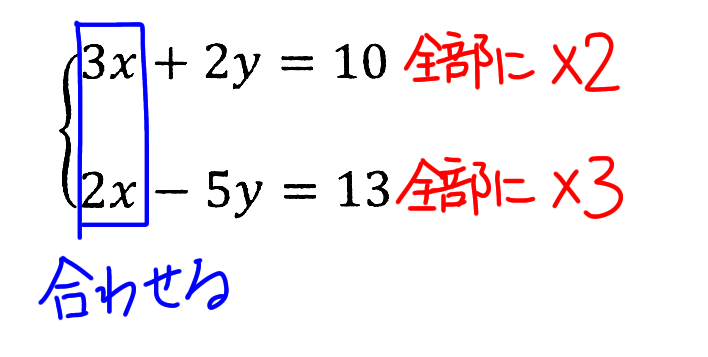
6に合わせるためには、3xの方を2倍、2xの方を3倍すれば、両方とも6xになりますよね。でもxの部分だけを 2倍、3倍としてしまったら、左辺(左側)=右辺(右側)だという式の性質が失われてしまいます。簡単に言うと、一部分だけに2倍とか3倍とかするのは不公平だということです。なので、この2倍、3倍というのは、それぞれの式全体を2倍、3倍しようという考え方になります。
上の式を2倍すると、6x+4y=20で、下の式を3倍すると、6x− 15y= 39(下図参照)。
これで式を足したり引いたりして計算しましょう。
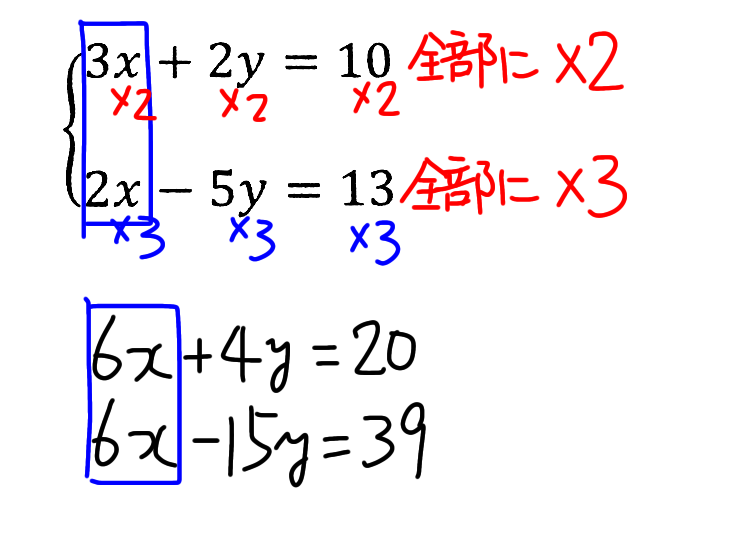
計算をするときのポイントとしては、この揃えたxを0にするように計算するのです。
両方ともxの係数(xの前についている数)は+6なので(前に+が省略されている)、足したら12になってしまいます。これでは消えません。消して0にするのが目的です。

そうするためには、引き算をします(下図参照)。

片方の答えを出すまで
引き算に決まりましたので上の式から下の式を引きます。ひき算になるということは、下の式に全部にマイナスがかかります。ひき算の場合、下の式全部の符号を逆転させるのを忘れないでください。そうすると、+6xと− 6xになるので、これでxが消えます。そして、yの方は、4y+15yで19y。イコールの右側の数字の方は+20と-39なので-19。そうすると19y=-19になるので、両辺を19で割ってやるとy=-1となります(下図参照)。

もう一つの答えを出すまで
y=− 1 っていうことが分かったので、これをどの式かに代入をしてxを出していきます。どの式に入れてもいいです。
でも、この一番下の式に入れるのはオススメしません。なぜ下はオススメしないかっていうと、この式のように引き算になってると、図を見ても分かるようにプラスがマイナスになったりマイナスがプラスになったりしてます。ゴチャゴチャしていますよね?こんな状態だと、元々どっちの符号だったのか分かりにくくてミスしやすいんです。だから一番下の式に入れるのはオススメしません。
オススメは元の式です。元々の式は、何倍とかしていないので式が簡単です。何倍かした式だと数が大きくなって複雑になる可能性があります。とはいえ、どれに入れても答えは出るので、やりやすいと判断した式に入れましょう。
ここでは1番上の式に入れることにします
1番上の式、3x+2y=10のyのところに− 1を入れます。そうすると、3x+2×(-1)=10となるので(下図参照)、
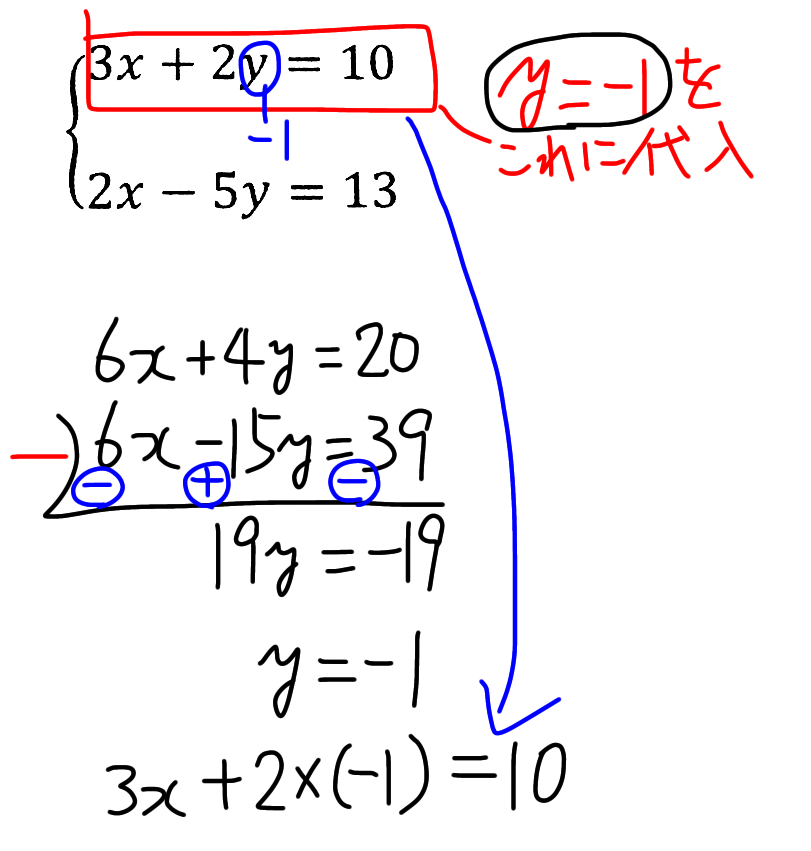
計算して3x-2=10。− 2 を移行して、3x= 10 +2。
3x= 12。xについている3で両辺を割って、x= 4。という感じでxの答えができます。そうすると答えはx=4,y=-1となって終了です(下図参照)。

これで一連の解き方は終了です。
でもここでは、今度はyの数字を合わせて解いた時の計算もやってみます。
もう一つの解き方もやってみます
同じ問題について違う解き方をしてみましょう。
今度はyを合わせたいと思ったとします。そうするとyに付いている数字の2と5を合わせるわけです。
ということは、上の式を5倍、下の式を2倍すればいいということになります(下図参照)。

そうすると上の式は15x+10 y= 50。下の式は2倍なんで4x−10y=26。今度はそろったyの符号が逆です。+10と − 10だったらこの時点でゼロになりますよね(下図参照)。
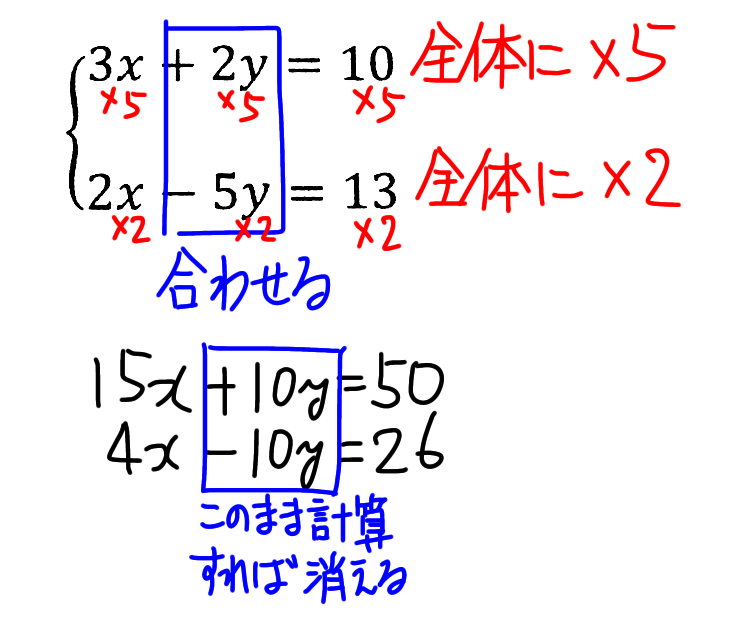
そうすると、今度は足し算ということになります(下図参照)。
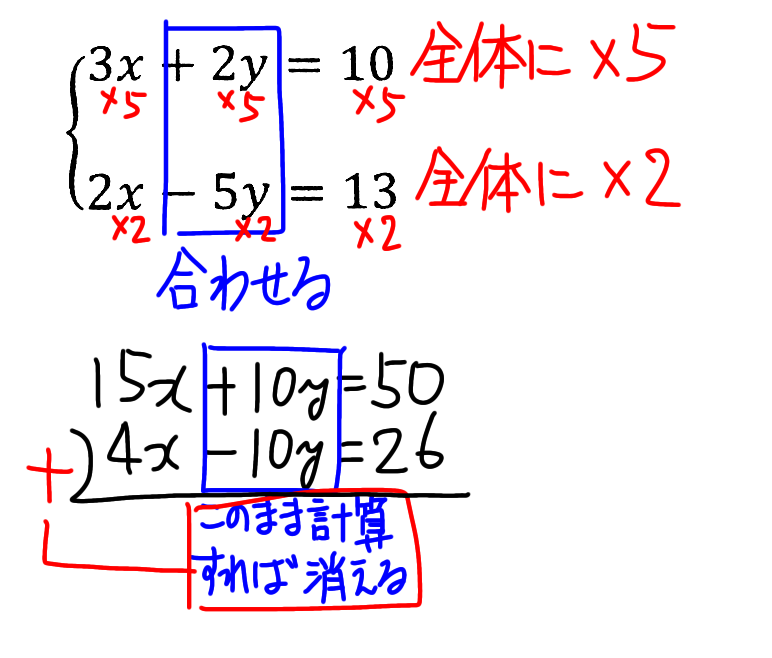
この2つの式を足すということは、下の式の符号を変えずにそのまま計算すればいいってことです。
そうすると19x=76。両辺を19で割って、x=4(下図参照)。

xが出たので、このx= 4をどれかの式に代入していきます。先ほども言ったように、本当は元々の式に入れて解いた方が数が大きくならないので計算しやすいのですが、ここでは、わざと数が大きくなった式、15x+10y = 50に入れてみましょう。どれに代入しても解けるということを実践してみたいと思います。
xに4を入れると、
15 × 4 +10 y = 50
60 +10y = 50
60を移項して
10y= 50 − 60
10y = − 10
y = − 1(下図参照)
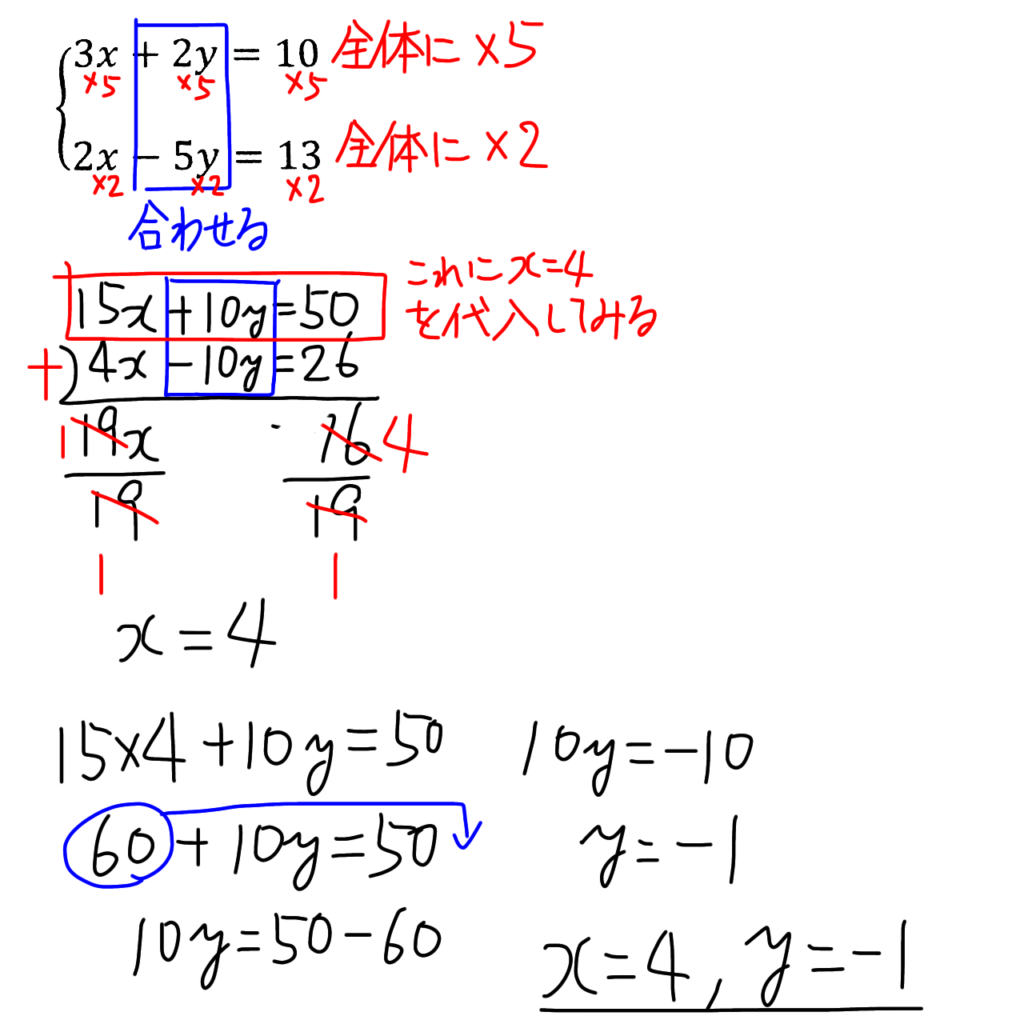
さっきの答えと同じになりました。そうならないとおかしいんですけどね。
この場合はそれほど複雑にならなくて済みましたが、式によっては何倍かした式に代入をすると、計算自体が複雑になって、計算ミスをしてしまう原因になることもあります。できるだけ簡単に計算しやすい式を選んで代入しましょう。
さて、それではいつでもこんな風に「どっちの式もかけ算して何倍かしなきゃいけないのか?」というと、もちろんそういうわけではありません。
目的はxか yか、どちらかに付いている数字をそろえることです。だから掛け算しなくてもxかyの数字がそろっているのだったら、そのまま足したり引いたりして答えを出せばいいですし、1つの式だけをかけ算をして数字がそろうのなら片方だけかけ算すればいいです。
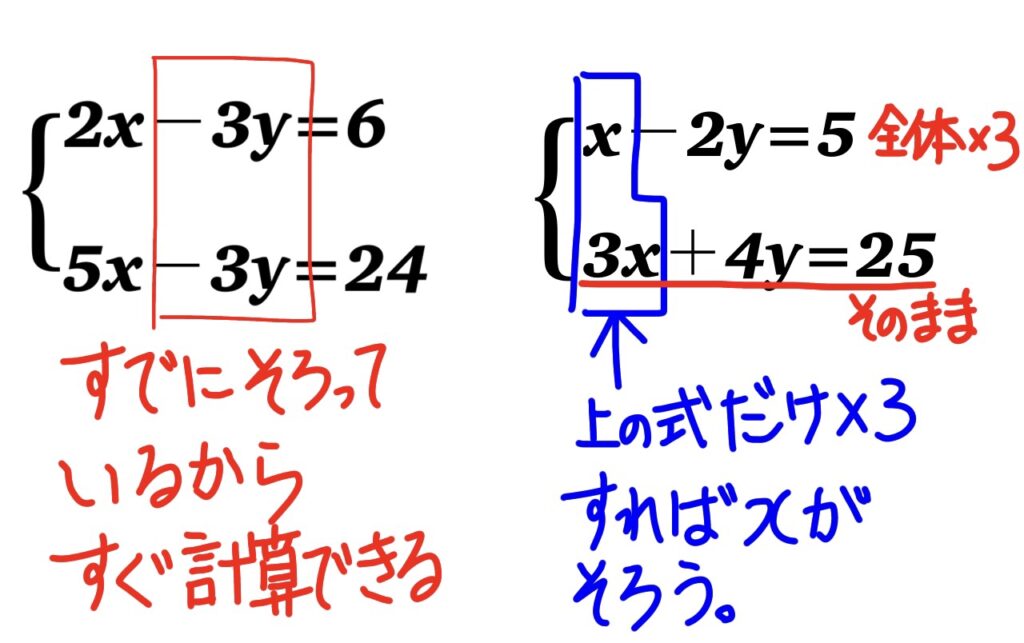
あくまで目的はxの数字かyの数字を同じにすることです。それを忘れないでください。
連立方程式(加減法)の注意点
1,数を何倍かするときは式全体を何倍かすること!
2,xかyかどちらかを同じ数にそろえるように何倍かすること!(しなくてもそろっていればそのまま計算してOK!)
3,2つの式を足すのか、引くのかの判断を間違えないようにすること!
4,計算は常に「+」なのか「ー」なのかを意識して計算すること!
5,符号を入れ替えたりして+かーかの区別がつきにくくなった式には代入しないこと!
なぜ2倍、3倍しても答えが出るの?
式を2倍するとか3倍するとかで答えが出せると言いましたけど、私が現役のとき思ってたんです。「2倍とか3倍とかしたら答えも2倍3倍になっちゃうんじゃないの?」って。同じように思っている人はいませんか?
なんで2倍3倍しても答えが出せるのかを説明します。興味がある人はご覧ください。
例えば、100円のもの3個買って、60円ものを2個買ったとします。300円と120円合わせて420円になります。(下図参照)
この式を全部2倍していきます。
そうすると計算はこうなります。
2×3 × 100円+2×2 × 60円=2×420
6×100円+4×60円=840
こうやって全部2倍したとしても金額(円のところ)は変わりません。

結局、式を何倍したところで、全部を同じ数をかけるんだったら、元々求めたい数は変わらないということですね。これは「等式の性質」を使っています。全部に同じものをかけたり、割ったりしても「=」になるということは変わらないんです。ですので、安心してかけたり割ったりしましょう。もちろん、「式全体を同じ数で」という制約は付きますけどね。


コメント