二次方程式の解き方の基本パターンを小分けにしてじっくり解説！

二次方程式には大きく分けて3つの解き方あります。

1、平方根を使った解き方

2、因数分解を使った解き方

3、解の公式を使った解き方

学校で習うのは1,3,2の順番です。しかし、解くときの順番としては1,2,3の順番で考えるのが一般的だと思います。

ここでは1,2,3の順番で説明をします。

平方根を利用した解き方

使われる場面	2乗の数と数字だけのとき（例：x²－16＝0）
解き方	数字を移項して「⬜︎² =数字」の形を作って2乗をはずす

例題１　ｘ²＝□

	数字を右辺に移項します
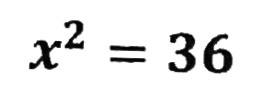	2乗して３６になる数は＋６とー６です
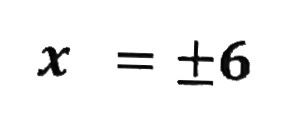	これで答えです。

一次方程式の場合、「x＝□」のように求めていきますが、この方法の場合は「x²＝□」という形を作って、「2乗すると36になる数は何か？」のように考える計算になります。例題2も見てみましょう。

例題2　〇ｘ²＝□

	まずは数字を移項します
	方程式と同じように x²＝□の形を作ります
	2乗して10になる数は 整数にはないので √　を使います
	これで終了です

x²に数字（係数）が付いている場合は、その係数で両辺を割って「x²＝□」の形に持ち込みます。ここまでの流れは、x² になっているだけで、一次方程式と同じ感覚ですね。そしてそこから平方根を求めて答えになります。

例題3　答えが分数になるタイプ

	数字が右辺にあるので、 x²＝□の形を作ります
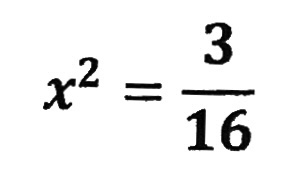	分数になった場合は、 分母と分子それぞれの平方根を 考えます。 16→±４、3→±√３なので
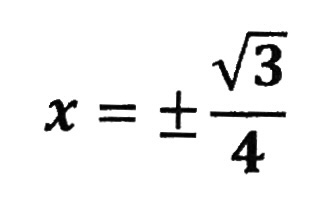	このようになって終了です

分数になっても同じことです。分数の場合は、分母と分子のそれぞれで平方根を考えるようになります。

ここまでが大丈夫そうであれば次をご覧ください。ここからはちょっと形が違います。ポイントは（x－□) や (x+□) のような（　　）をひとまとまりの数と見ることです。

例題4　( )²＝□（答えが整数）

	（　）内を「１つの文字」 と考えて数字を移項します
	2乗して36になる数を 考えて2乗をはずします
	これでー3が 移項できますので、 移項します
	両方が整数なら、 足し算、引き算が できるので ＋とーに分けて 計算します
	３＋６＝９、 ３－６＝ー３ なので
	これで終了です

例題5　( )²＝□（答えに√を含む）

	2乗して18になる数を 考えて 2乗をはずします。
	これで＋２が移項 できますので、 移項します。
	√ の外に出せるものが あれば出します。
	整数と√　はこれ以上 計算できないので、 これで終了です。

ここまでが「平方根を利用した解き方」です。使える場面は少ないですが、この解き方ができる場合はこの解き方が一番簡単です。覚えておきましょう。

因数分解を利用した解き方

この解き方をする時は、必ず右辺が0であることを確認して解きましょう！

例題1　( )( )=0にするパターン

	左辺を因数分解します。 たしてー3、かけて―10 なので、 ー５と＋２です。
	(x-5)と(x+2)のかけ算を 意味しています。 (x-5)か(x+2)のどちらか が０でない限り、 かけて０には ならないので どちらかが０です。
	あとは数字を 移項すれば 答えになります。
	これで終了です。

これが基本に則した解き方です。この理屈が分かっていれば、因数分解をした後、「符号を逆転して答え」というように考えても問題はないでしょう。

（x－5)(x+2)=0 ⇐符号を逆にして

x=5 , x=－2 ⇐すぐに答えを出してもOKです。

ただ、これは「x－5=0、x+2=0 のそれぞれの方程式を解いて移項したから、結果的に符号が逆転することになるんだ」という理屈は頭の片隅に入れておいてください。それが頭に入っていれば、下の例題2のような場合でも同じように解けます。

例題2（すでに因数分解されているパターン）

	もうすでに 因数分解されています。 展開しないように 注意しましょう。
	例題1と同じです。 どちらかが０に なります。
	あとは、 方程式の要領で 解きましょう。
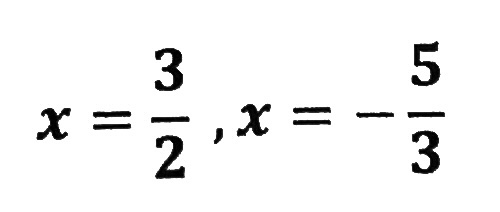	これで終了です。

この後の「例題3」「例題4」は、考え方は同じですが、初めてだと「どうやるんだ？」と思うかもしれないので、答えの出し方や考え方を確認しておいてください。

例題3　( )²＝０になるパターン

	乗法公式を用いても 良いですし、 たしてー６、 かけて９ で因数分解しても OKです。
	この式は、 (x-3)(x-3)=0 の意味です。
	どちらかが ０になります。
	しかし、 どちらも同じ式 なので
	同じ答えに なります。
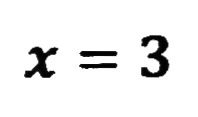	その時は、 答えは１つで OKです。

例題4　共通因数でくくるパターン

	xが共通しているので、 xでくくります。
	xと(x-5)のかけ算を 意味しています。
	どちらかが０に なるので
	答えはこうなります。

例題4のような共通因数でくくる因数分解は忘れられがちなので、しっかり頭に留めておいてください。

解の公式を使った解き方

この解き方をする時も、必ず右辺が0であることを確認して解きましょう！

覚えよう！解の公式

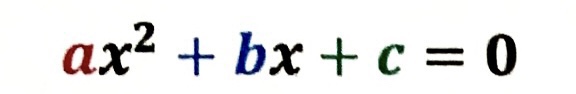
x²の係数をa、xの係数をb、それ以外（定数項）をc としたとき、それらを代入すれば二次方程式はすべて解けるというありがたい公式が「解の公式」です。

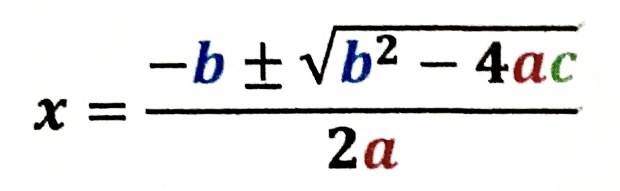
ちょっと複雑ですよね。でも、歴代の中3生はみんなこれを覚えて解いています。何題か練習すれば自然と覚えるので、練習して覚えていきましょう。

例題1　普通に計算を頑張れば解けるパターン

	解の公式に 入れてみましょう。
	a=2,b=－1,c=－5 です。 公式にそれぞれを 入れます。
	√ の中は、 2乗とかけ算を 先に行いましょう。
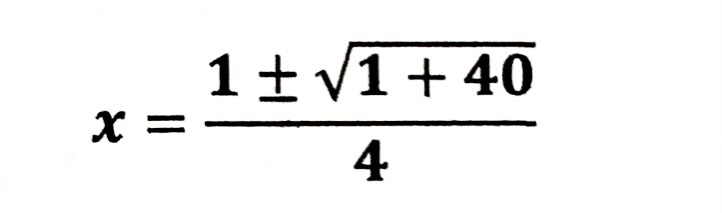	√ の中をまとめます。
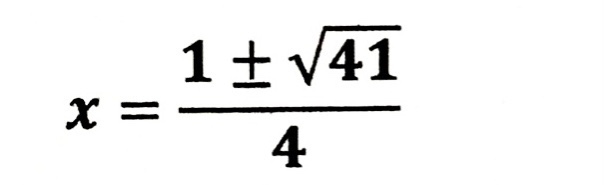	複雑に見えますが、 慣れるまで 繰り返し ましょう。

例題2　最後に約分をするパターン

	xの係数が偶数の時は 最後に約分を することになるので 注意しましょう。
	a=1, b=2, c=－7を 解の公式に入れて いきます。
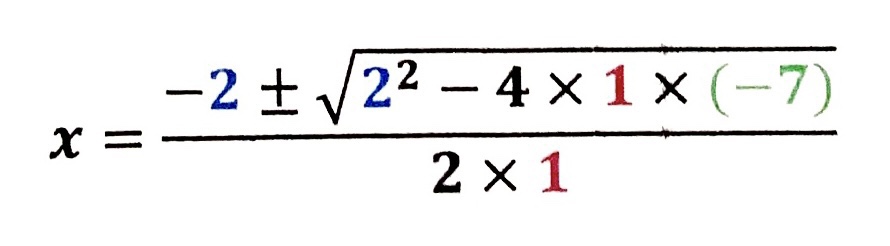	例1と同じ要領で 計算をします。
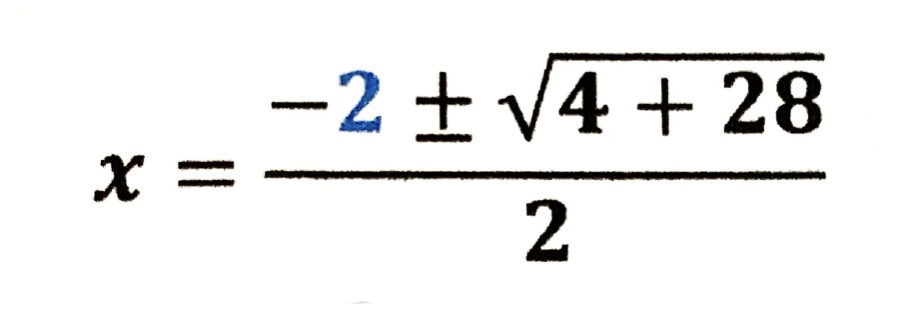	√ の中をまとめると…
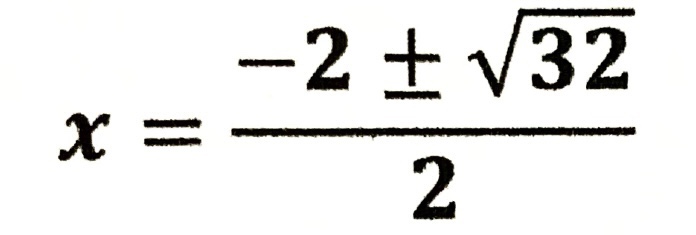	√ の中が簡単にできます。 □√○の形にできるものは 必ずしなければ なりません。
	各整数が2の倍数に なりました。 こういう時には 約分ができます。
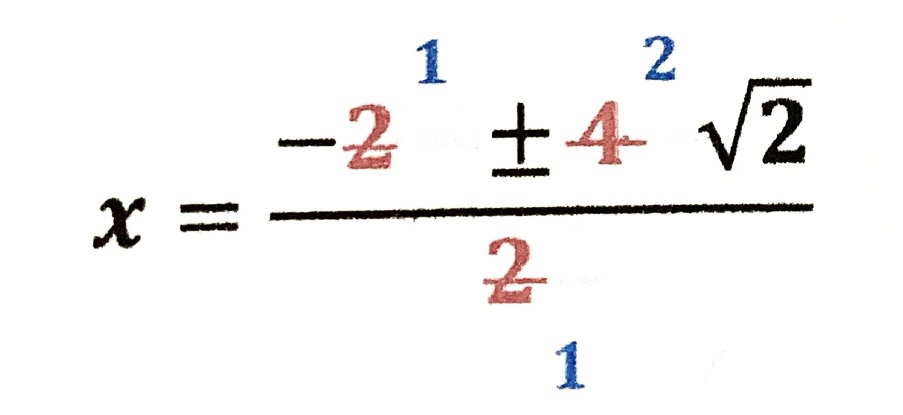	全部を一気に 約分します。
	分母が１になった ので、省略して 答えになります。

なぜ全部一緒に約分しないといけないのか

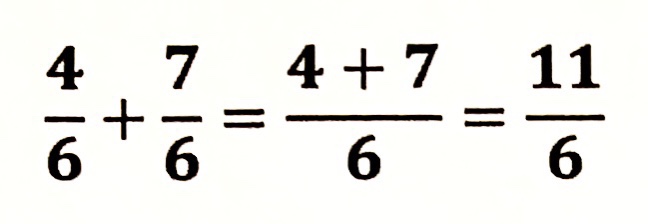○		普通に計算した答え
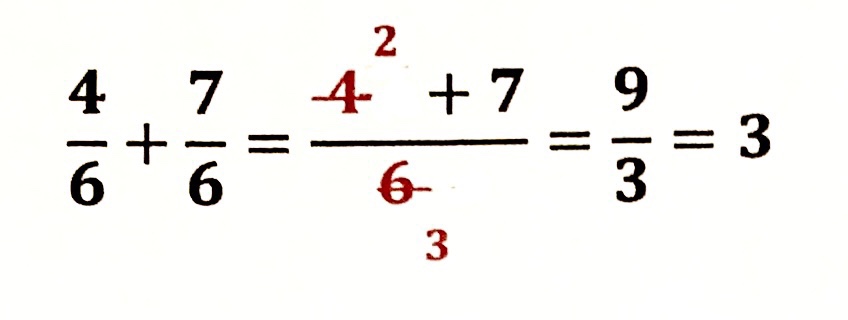×		片方だけ約分するとこうなる

分母は2つの数（ここでは４と７）の共通の分母です。片方だけで約分してしまうと、もう片方の分母も変わってしまいます。 だったのに、いつの間にか に変化しちゃってるのです。これでは計算が違ってしまいます。

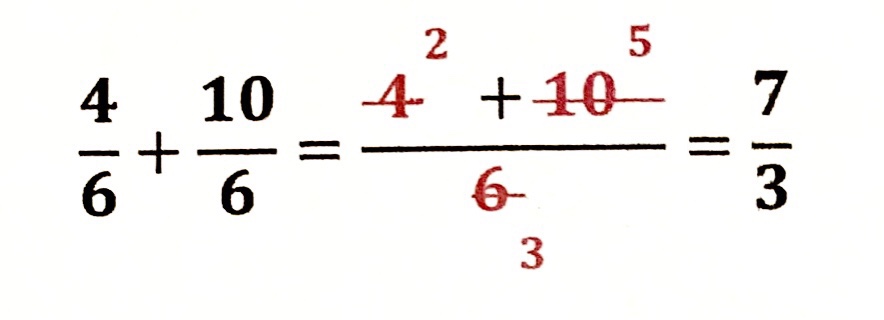	両方を一緒に約分 するなら、 どちらも平等に 約分されるので 問題ありません。
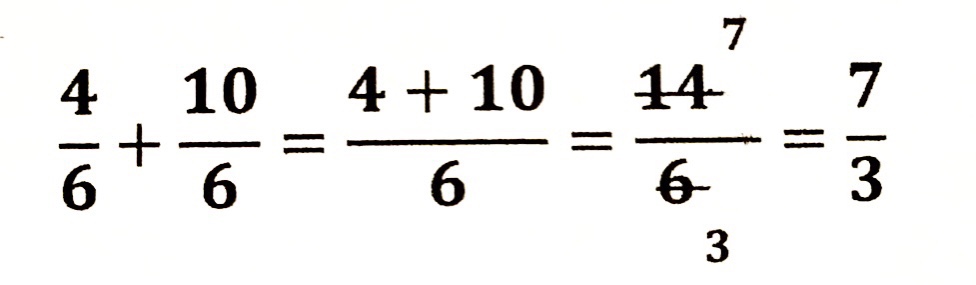	普通に計算したものと 答えも同じになります。

これは解の公式を使う時だけでなく、数学全般で使う計算方法なので覚えておきましょう。

こう考えれば…

二次方程式は究極的には「解の公式」を使えば全部解けます。

①平方根を使うパターンで紹介したこの式

x²－36＝0⇒１x²＋０x－３６=0

こう考えれば、解の公式に入れて解くことができます。また、

x²－36＝0⇒(x－6)(x＋6)=0

とすれば、因数分解の考えでも解けます。

②（x－3)²－36＝0

このパターンも、式を展開して

x²－6x＋9－36＝0

x²－6x－27＝0

（x－9)(x＋3)＝0

と、していけば因数分解でも解けますし、もちろん解の公式に入れて解くことだってできます。

「何個も方法があると、どれを使ったらいいか分からなくなる。」

ではなく、

「簡単な方法で解けるなら解いて、できないなら最終手段解の公式」と考えてみましょう。イメージとしては、

先制攻撃	平方根
メイン武器	因数分解
必殺技	解の公式

こんな感じです。

①平方根の解き方が使える問題は

x²－数字=0

( )²ー数字=0

この２パターンに限られているので、最初に使えるかどうかを見た目で判断

②平方根パターンでなければ因数分解で解く！

③それも無理なら必殺！解の公式！

そんな感覚でやってみると良いと思います。