20年以上の授業の中で体験したよくあるミスを挙げていきます。式の計算は色々なミスが出やすいところです。
「人のふり見て我がふり直せ」という言葉がありますが、間違いに気をつけて解くことで正解率は向上します。どのように計算すれば良いのかを理解していきましょう。
【よくあるミス①】符号のミス
間違い例
\(\left( 3x-4y\right) -\left( 2x-3y\right) =\)\(3x-4y-2x-3y\)
このようにしてしまうミスがよくあります。
本当は
\(\left( 3x-4y\right) -\left( 2x-3y\right) =3x-4y-2x+3y\)
このようになるのが正解です。
方法は正負の数と同じです。( )の前のマイナスをプラスに変えたら、後ろの( )の中の符号は全部逆になります。
( )の間の符号を+に直して、後ろの( )内の符号を変えてから( )をはずして計算しましょう。
(3x−4y)−(2x−3y)
=(3x-4y)+(-2x+3y) ⇐( )の前の符号を+にして、( )内の符号を逆にする
=3x-4y-2x+3y ⇐かっこをはずす
=3x-2x-4y+3y ⇐文字の同じもの同士(同類項)を集める
=1x-1y ⇐同類項を計算する
=x-y ⇐文字の前が1になったら1は省略。
これは分かっていてもうっかりやってしまいがちなミスです。マイナスが出てきたら注意して解きましょう。
【よくあるミス②】xが残ってしまうミス
間違い例
\(2x-2x=x\)
このミスもよくあります。
2 − 2 = 0です。
この計算は0xとなりますが、0 は何をかけても0なので、xをかけても0です。ですから、xも消えます。
\(2x-2x=0\)
これが正解です。
よく出題される問題にはこのようなものがあります。
\(2x-3y-5x+3y\)
これを計算していくとこうなります。
2x-3y-5x+3y
=2x-5x-3y+3y ⇐同類項を集める
=-3x ⇐-3y+3y=0になって消えます!
【よくあるミス③】( )内の累乗のミス
間違い例
\(\left( 3x\right) ^{2}=3x^{2}\)
( )の中が掛け算の式の場合、2乗は数字にまで効果が及びます。数字も文字も全部を2乗しましょう。
(3x)² ⇦( )の外に2乗がある時が注意!
=3²×x² ⇦どちらも2乗します。
=9x²
これが正解です。
【よくあるミス④】分母と分子が混ざってしまうミス
間違い例
\(15ab\div 5a^{2}b=3a\)
文字式の割り算は分数にして計算をしましょう!分数に抵抗がある人もいるかもしれませんが、使い方によっては分数は結構使えるヤツです!
そして分母に残れば分母の数。分子に残れば分子の数です!それ以上計算してまとめないように気をつけましょう。
\(15ab\div5a^{2}b=\dfrac{15ab}{5a^{2}b}\ =\dfrac{3}{a}\)
このような計算になります。
こうやって分数にすると分子と分母が明確になるので 、間違いが少なくなります。分数にしないで頭の中で計算したり…
315ab÷5a²b
このように問題文を約分していくだけで求めようとしたりすると、「3a」って答えたくなっちゃいますので、文字式の割り算は分数にして計算しましょう。
【よくあるミス⑤】うしろのかけ算を先に計算してしまう
間違い例
\(6x^{2}y^{2}\div 2xy\times 3x\)
\(=6x^{2}y^{2}\div 6x^{2}y\)
\(=y\)
これもよくある間違いの一つです。
「割り算と掛け算は同じ順番だから、どっちを先に計算してもいいじゃん!」と思うかもしれませんが、前から順序よく計算していくと、答えが違うことがわかります。
6x²y²÷2xy×3x ⇦前の割り算を計算して
=3xy×3x ⇦かけ算して
=9x²y ⇦答えです
これが正解になります。
なぜこのような間違いになってしまうのか?
これは、割り算をかけ算に変えると、÷の記号の後ろの数だけが逆数になるからです。
\(\dfrac{6x^{2}y^{2}}{1}\times \dfrac{1}{2xy}\times \frac{3x}{1}\)
こうして見ると何が間違いなのか気付くと思います。
最初に後ろのかけ算をするということは分母の2xyと分子の3xをかけてしまっているのです。それが間違いの原因なわけですね。
そのような間違いを避けるためには、かけ算割り算は全部一気に分数にして計算しましょう。そうするとこの間違いを防げます。

このような感じです。
④と⑤のミスは、分数を用いることで解消されます。
【たまにあるミス①】分数のたし算・引き算で通分しない
間違い例
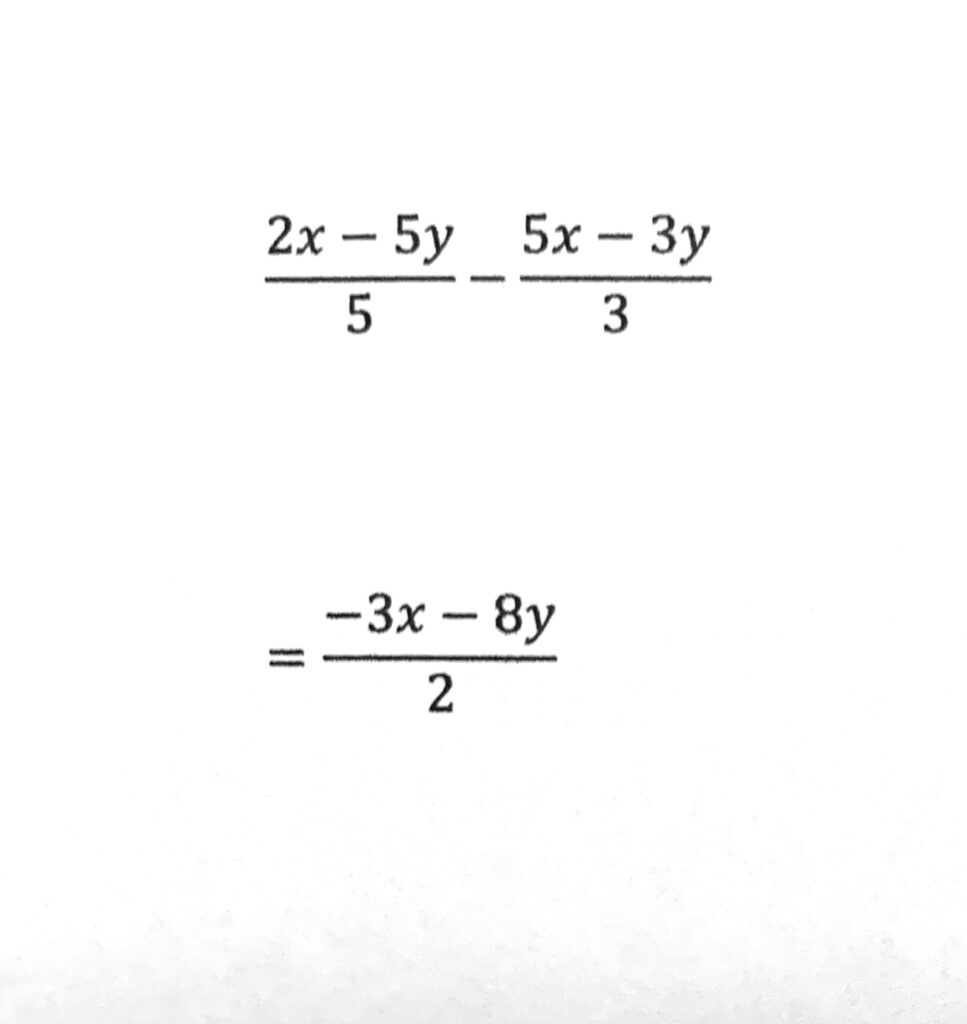
このように、分数を通分せず、分母は分母、分子は分子で足し引きしてしまう間違いです。
分数のたし算引き算は通分して計算しないと計算できませんので注意しましょう。
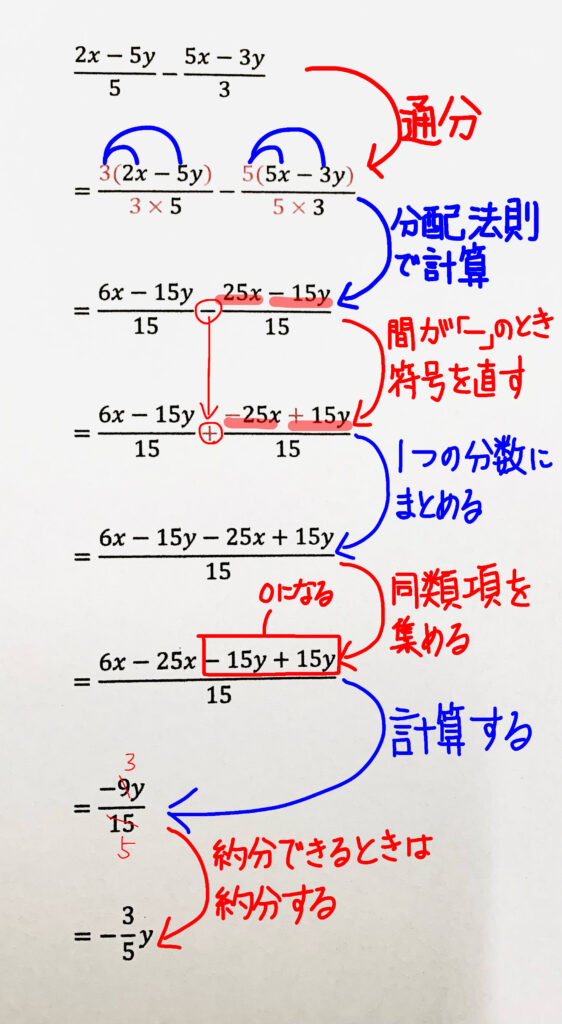
文字式になると普通の分数とは違う計算のように感じてしまう人もいると思いますが、小学校からやってきた通分と何も違いはありません。分母と分子に同じ数をかけて、分母の数を合わせればいいだけです。
ただ、上の例題は、分数以外にも「ー」を「+」に変える計算、0xになる計算もあるので、間違いやすいものの集合体ですね!これまで挙げてきた間違いやすいところの総復習として確認してみて下さい。
<分数補足>分数の約分で間違いやすいところ
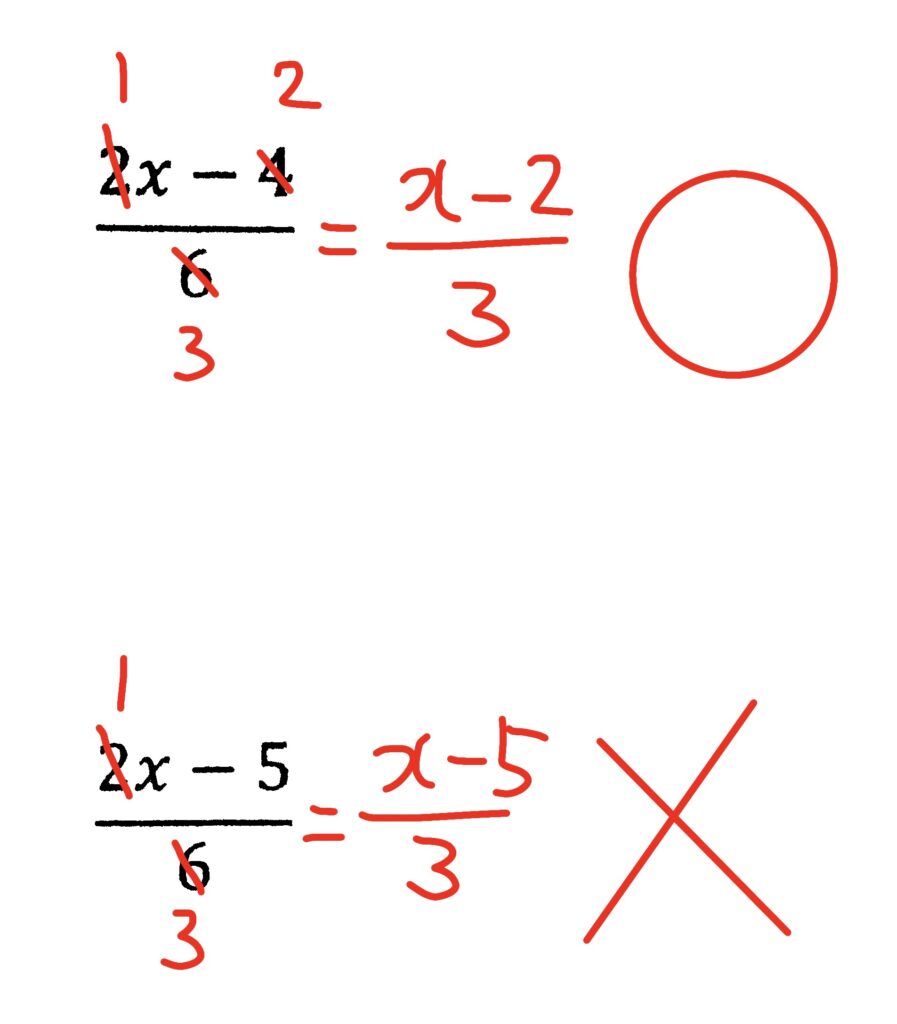
上の式のように、全部が一緒に約分できる時は約分できますが、下の式のように、片方しか約分できない場合は約分はできません。
それはなぜでしょう?下の計算をご覧ください。

上の式は約分できますが、下の式が約分できない理由がお分かりいただけたでしょうか。
分数の足し引きの場合は、分母が分子の2つの項(上の例では2xとー5y)の共通の分母なので、片方の都合だけで約分できない、ということですね。
よくやってしまいがちなミスなので注意しましょう。
【たまにあるミス②】分配法則を使用する時のミス
間違い例
2(3x-4y)+(2x-3y)=6x-8y+4x-6y
このように、先頭の数字を全部にかけてしまうミスです。
分配法則で掛け算をするのは、直後にある( )にだけです。「+」や「ー」でつながれたあとのものにまでかけないように気をつけましょう。
2(3x-4y)+(2x-3y) ⇐( )で閉じられている分にだけかける
=6x-8y+2x-3y ⇦分配法則の計算
=6x+2xー8y-3y ⇦同類項を集める
=8x-11y ⇦まとめて答え
このようになりますので、間違えてしまう人は気をつけて下さい。
この他に、同類項じゃないのにまとめてしまうミスという、すごくやりがちな特Aクラスのミスがあります。でもこれは別記事で詳しく説明したいと思います!


コメント