【三角形の合同条件】なぜそれで合同だと言えるのか？を徹底解説

①３組の辺がそれぞれ等しい

３つとも辺が等しければ合同である。…この条件に疑う余地はないですね。

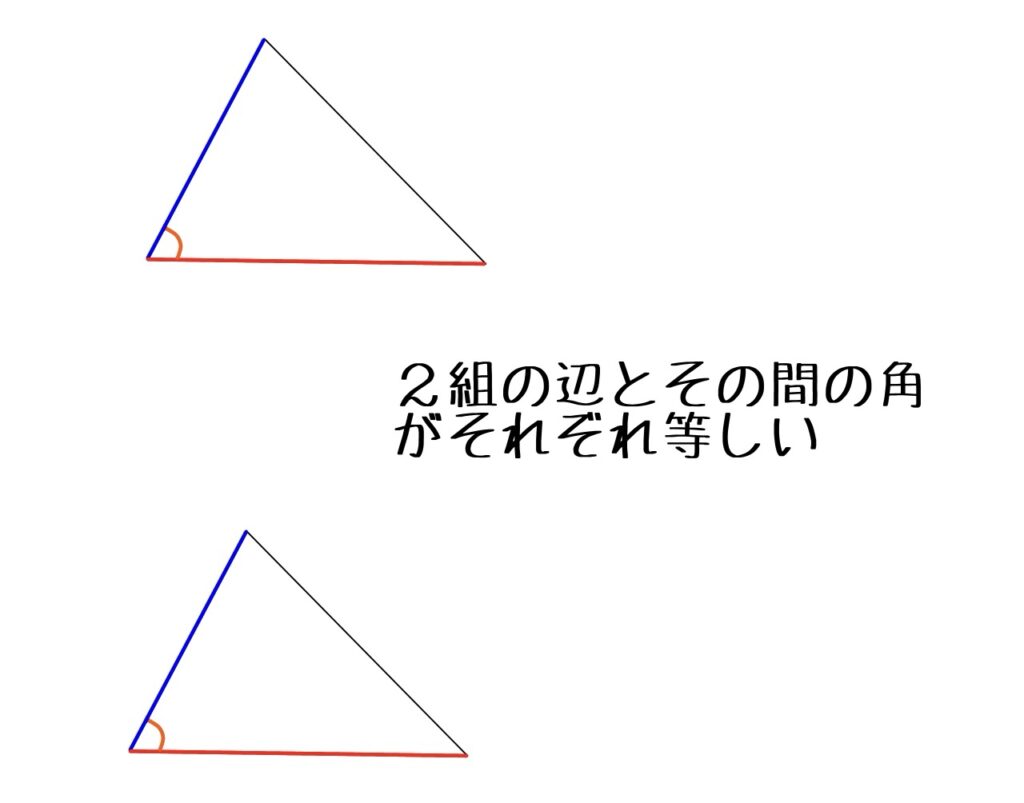
②２組の辺とその間の角がそれぞれ等しい

絶対「２辺の間の角」でないといけません。詳しくは後ほど。

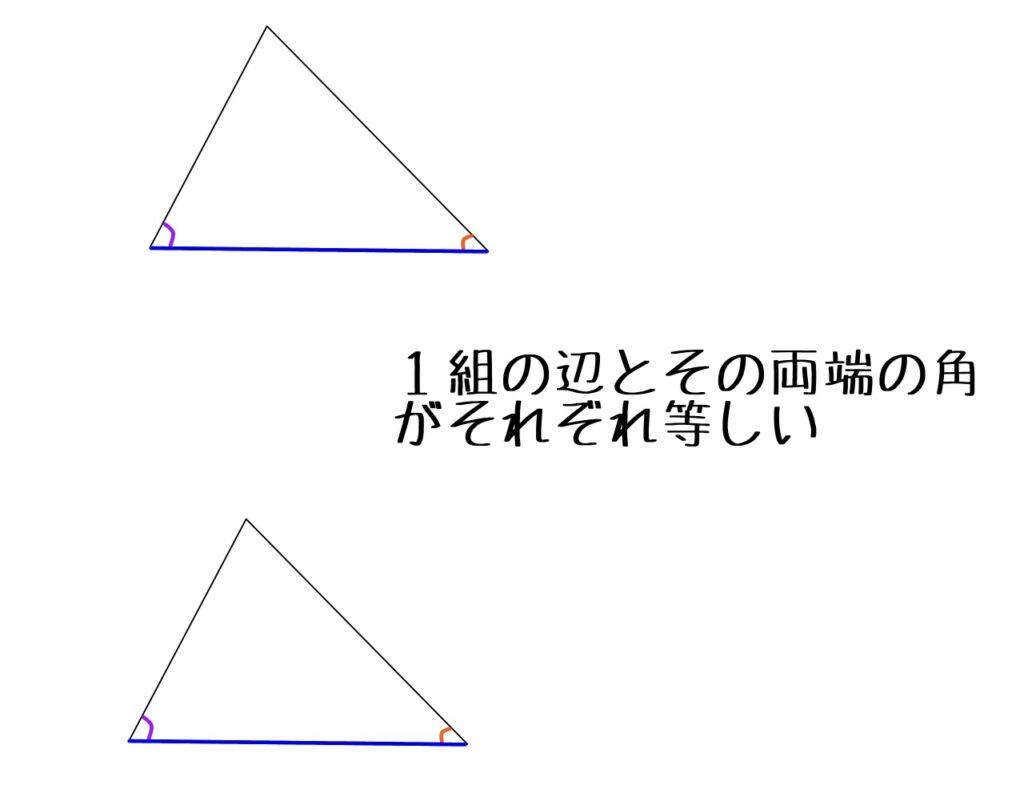
③１組の辺とその両端の角がそれぞれ等しい

絶対「両端の角」でなければならないのか？…というと、そうでもありません。詳しくは後ほど。

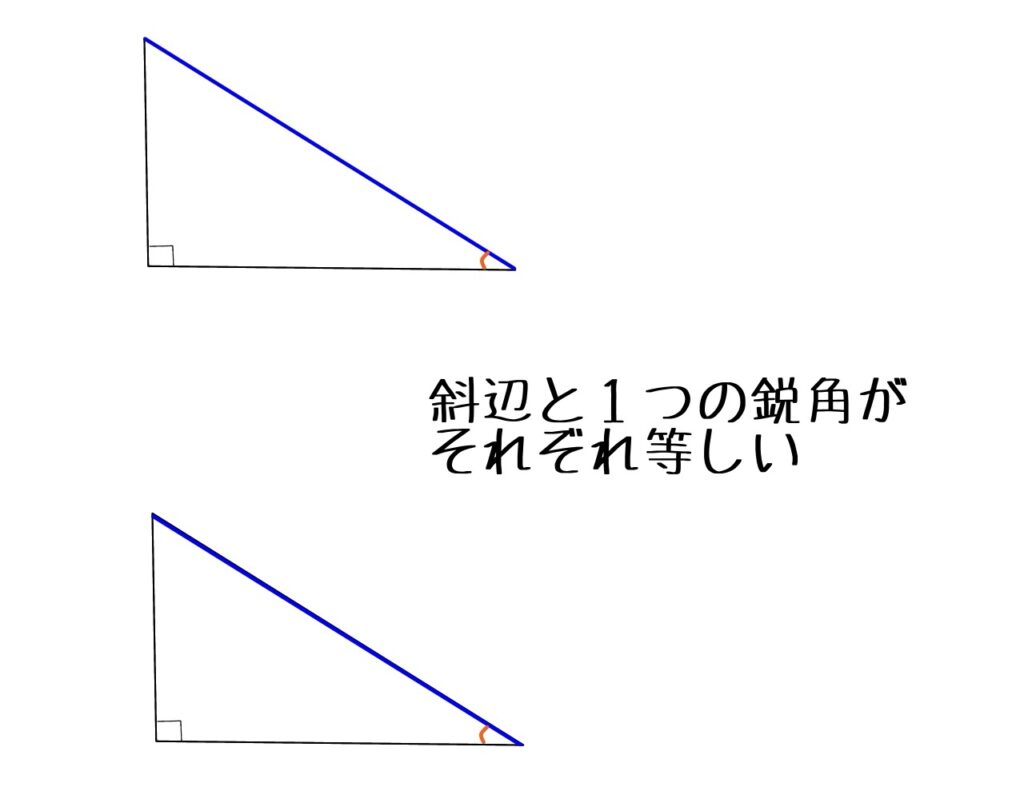
④斜辺と１つの鋭角がそれぞれ等しい

直角三角形の合同条件は必ず「斜辺が等しい」ことが必要です。それはなぜか？

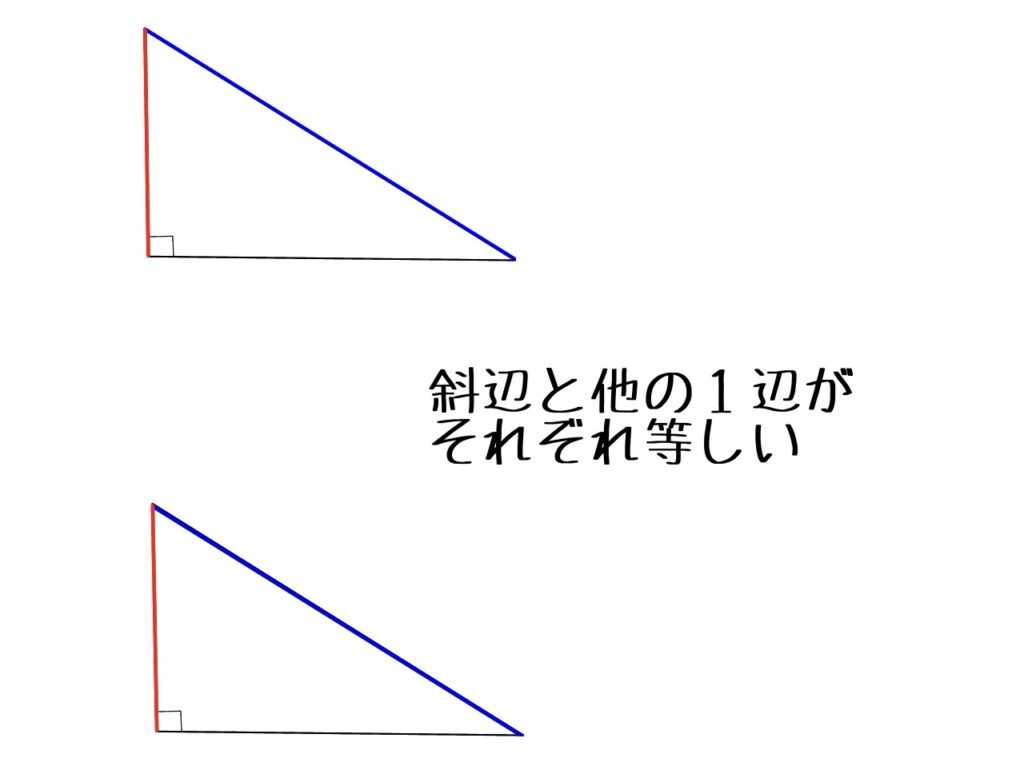
⑤斜辺と他の一辺がそれぞれ等しい

なぜこれで合同だと言えるのか？後で紹介します。

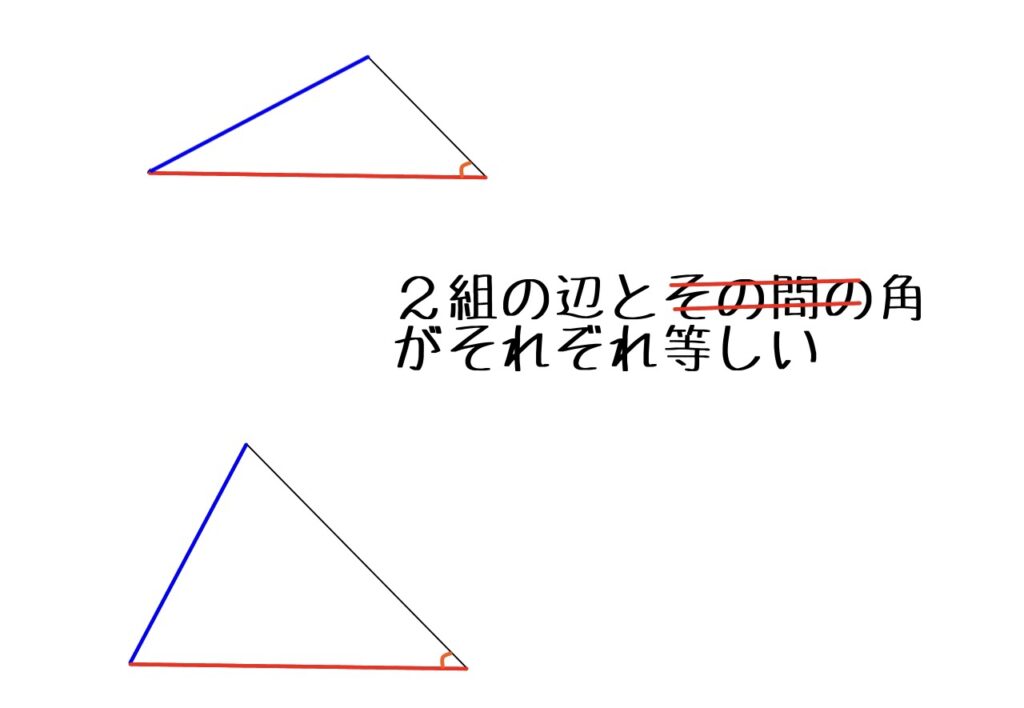
青の線、赤の線は同じ長さです。そして、赤の線の右側の角度も同じです。

２組の辺と１つの角は同じですが、ご覧のように２つの三角形は合同ではありません。

このような場合が存在するから、「必ず合同になる」とは言えないのです。

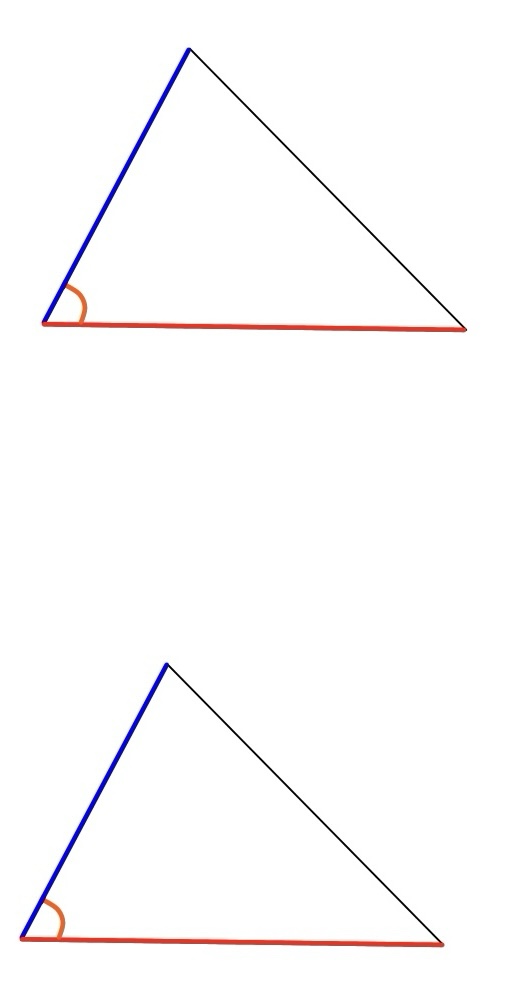
しかし、この図のように、赤の線と青の線の長さが決まっていて、間の角が決まっていれば、三角形を作るには、線の端同士を結ぶしかありません。どうやっても同じ三角形（合同な三角形）になってしまうのです。

だから、２つの三角形が「必ず」合同であるためには、「２組の辺の間の角」であることが必要になります。

逆に言えば、「間の角」でなければ、「必ず合同」とは言えないのです。

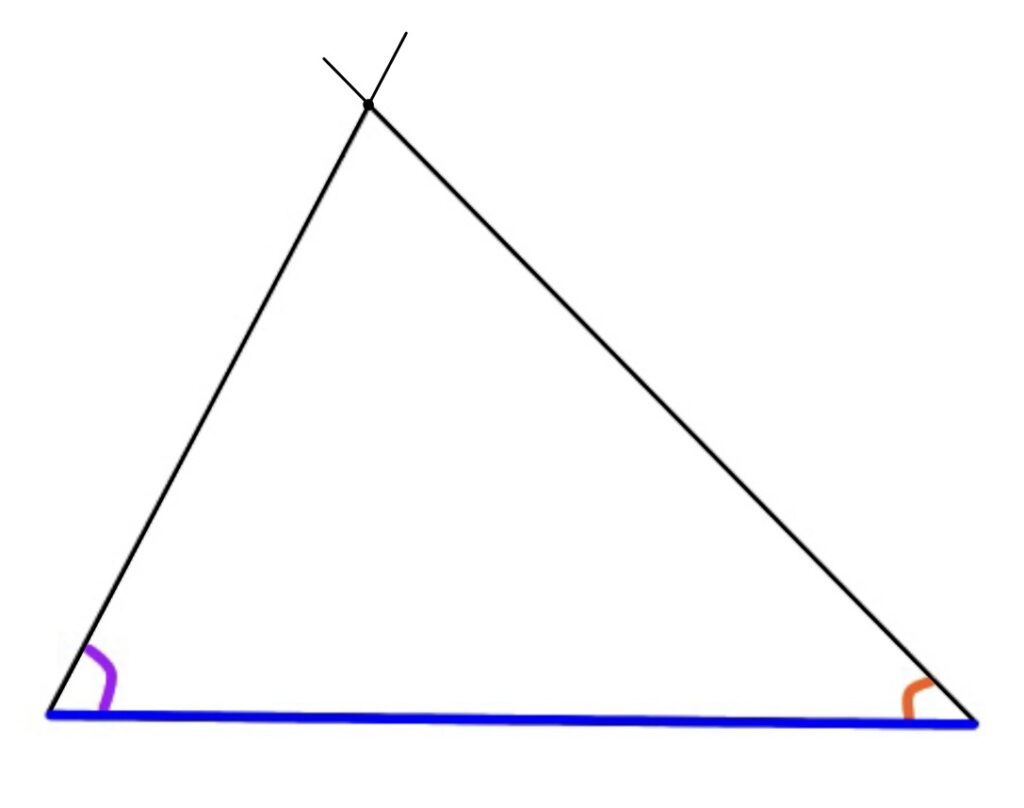
１つの辺の長さを決め（青線）、その両端の角度を決めて三角形を書くと、他の２辺も方向が決まります。

その方向にまっすぐ線を書いていくと、２つの辺が自然に交わる点ができます。

つまり、どうやっても１つの三角形しか書くことができないのです。

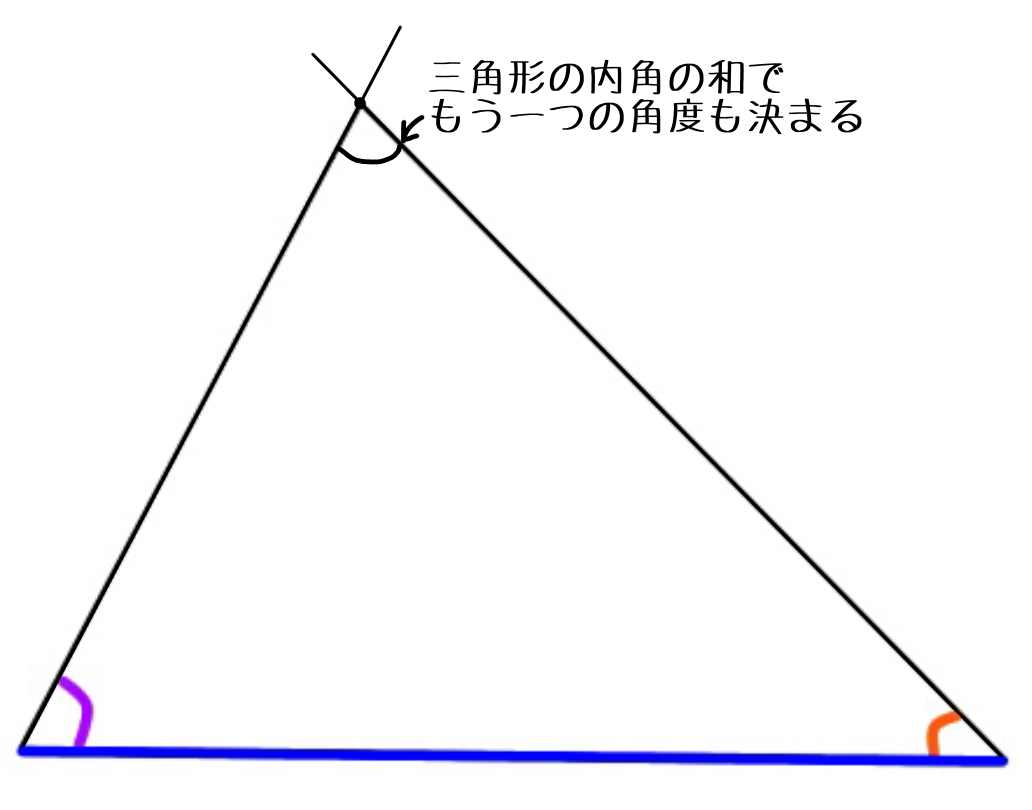
しかも、２つの角度が決まっているということは、三角形の内角の和は１８０°なので、もう１つの角度も決まります。

結局、２つの角が同じということは、3つとも角が同じということなのです。

さて、３つとも角が同じなのに合同でない図形はどういう図形でしょうか？

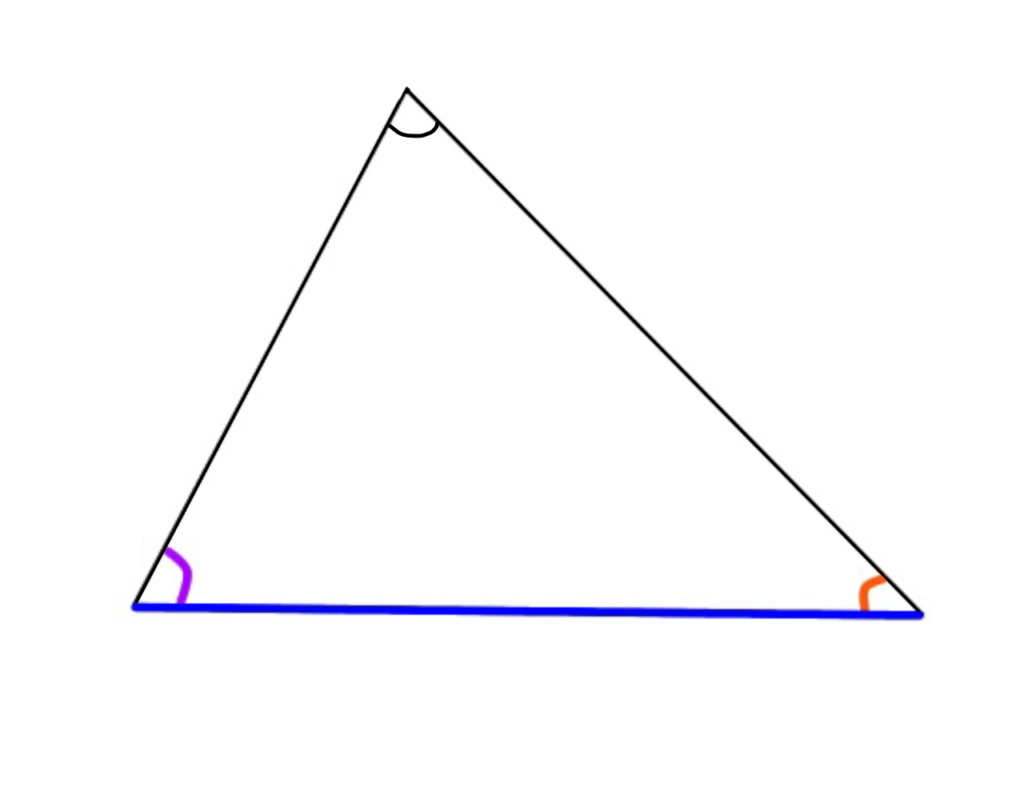
それはこういう図形です。

形状は全く同じですが、辺の長さが違うのです。

だから合同であるためには「１組の辺」の長さが同じであることが要求されるわけですね。

逆に言えば、必ずしも「両端の角」が分からなくても、２つの角が等しければ、もう一つの角も必ず等しくなります。１つの辺が等しくて、２つの角が等しければ両端でなくても理論上合同が成立します。

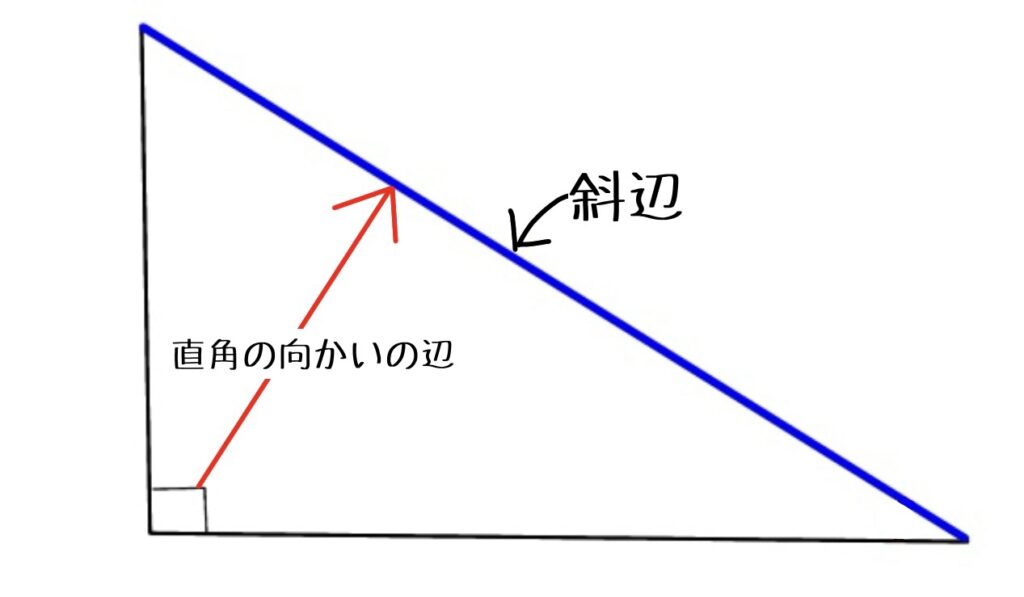
直角の向かい側の辺を「斜辺」と言います。

「ななめに見える辺」ではないので注意してください。

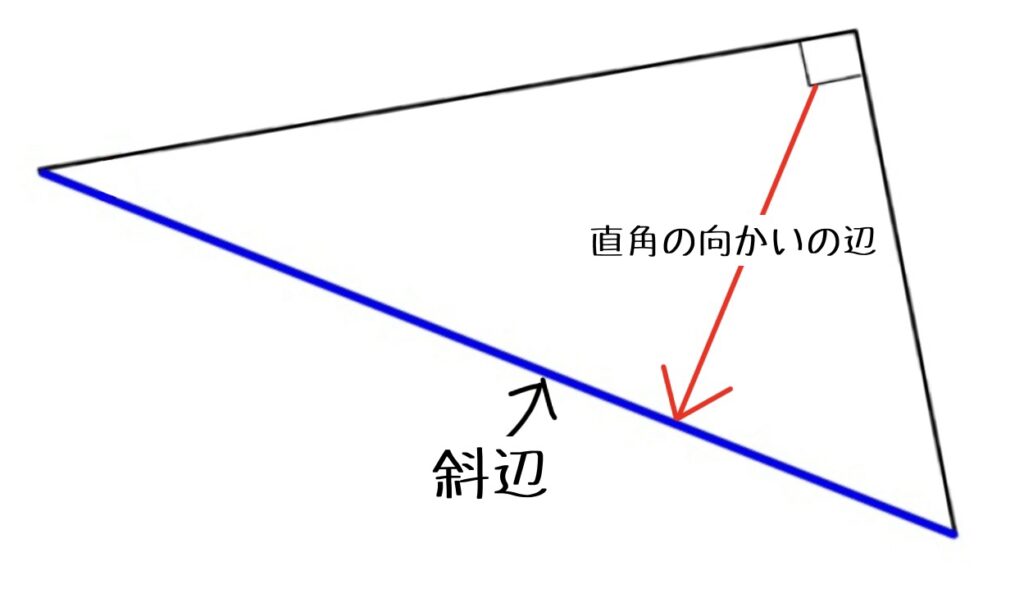
このような三角形でも「斜辺」は直角の向かいの辺です。

直角三角形の合同条件を使うには、この「斜辺」が重要になります。斜辺の位置を間違いなく覚えておきましょう。

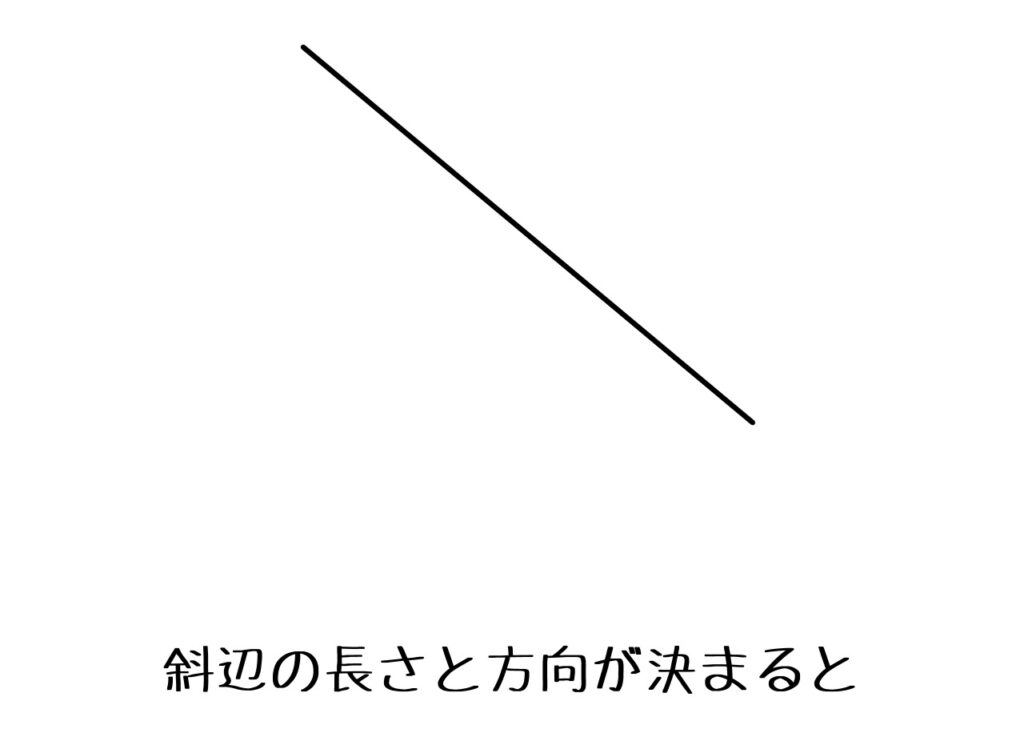
このように、直角三角形の斜辺の長さと方向が決まったとしましょう。

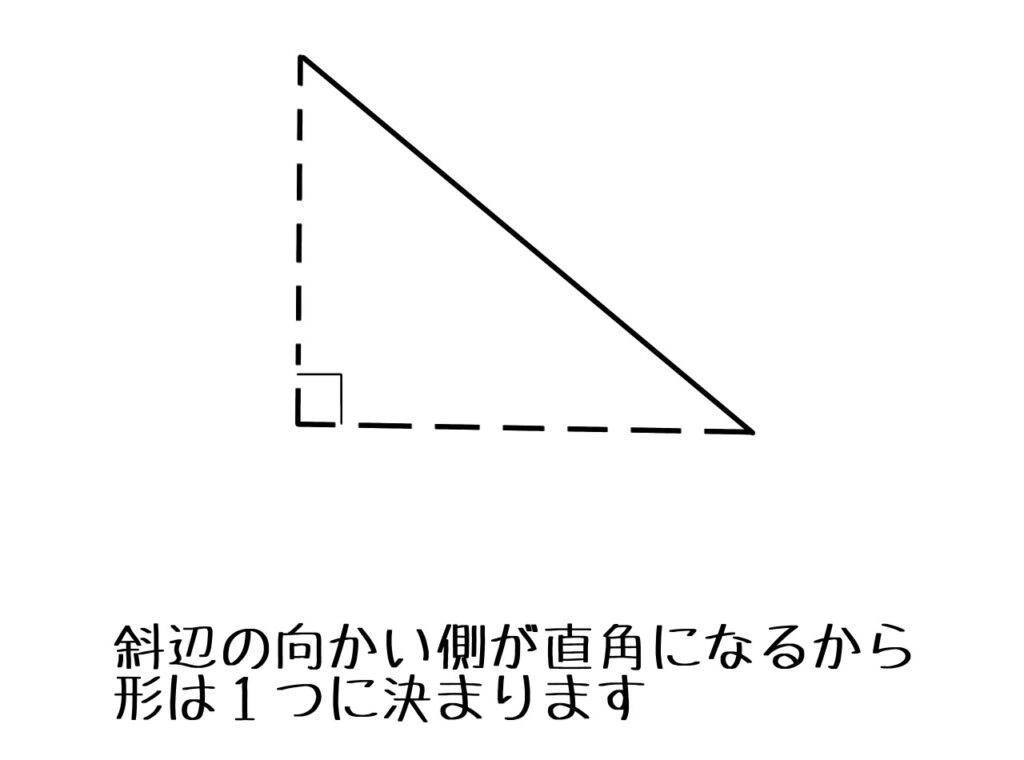
そうすると、斜辺の向かい側が直角になるのが直角三角形なので、線の両端から出る線は１つに決まります。

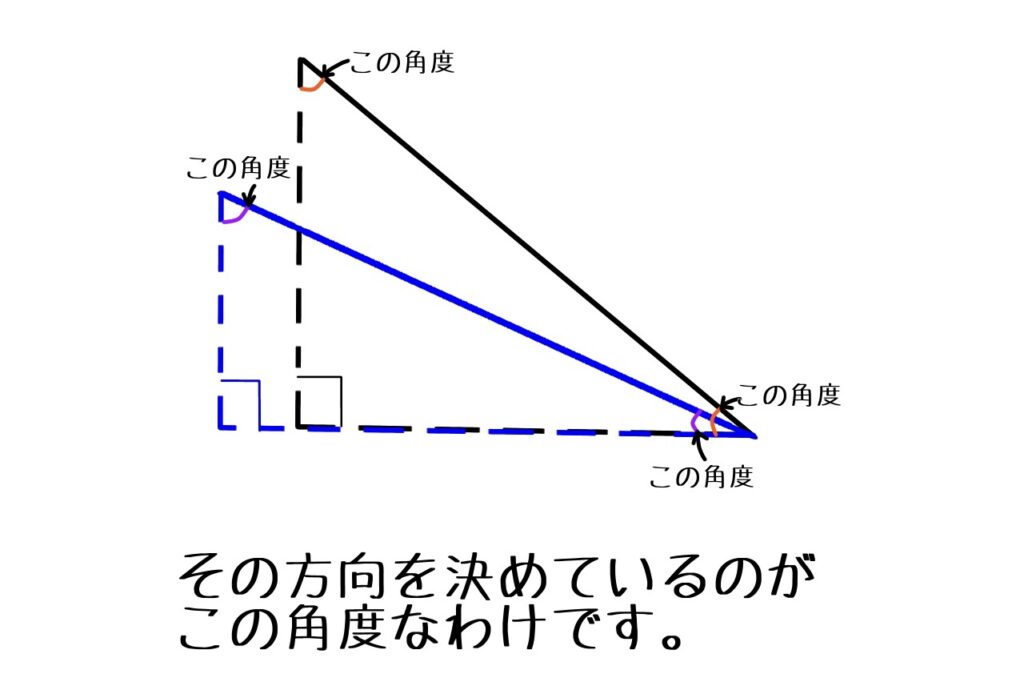
ご覧のように斜辺の長さが同じでも、角度が変わると違う三角形になります。だから１つの角が同じであることが必要なのです。

直角以外の１つの角が同じなら、三角形の内角の和は１８０°と決まっているので、もう１つの角も必ず同じになります。ですから、三角形は絶対合同になります。

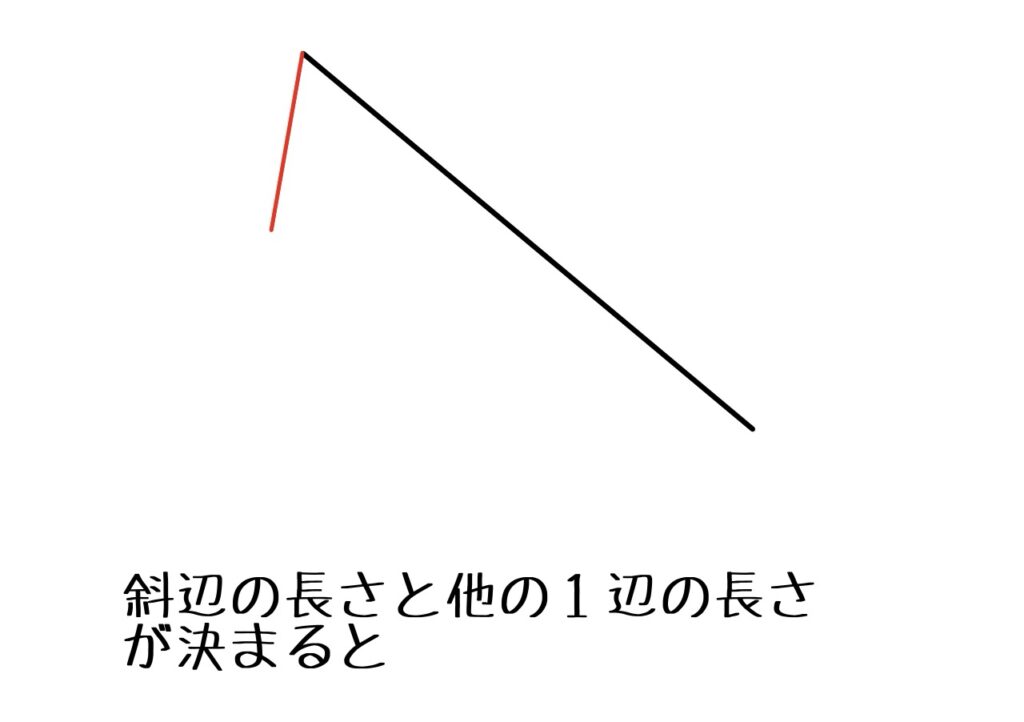
このように、斜辺と他の一辺の長さが決まったとしましょう。

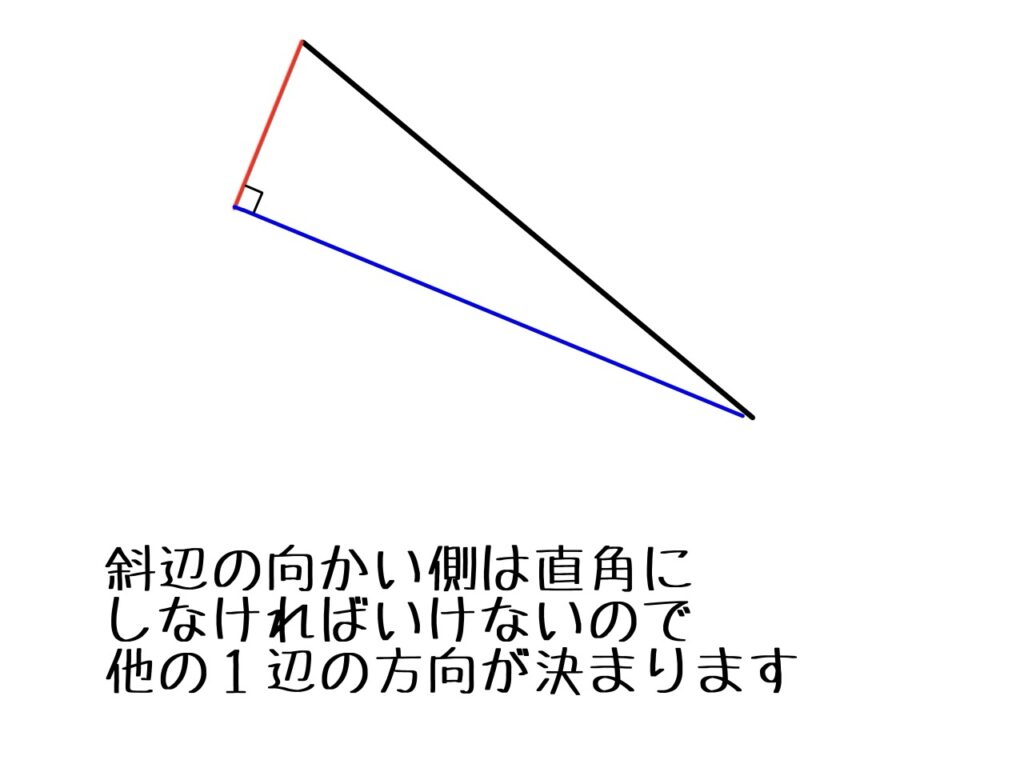
そうすると、斜辺の向かい側は直角にしなければならないので、長さが決まった一辺の方向と、それ以外の辺の長さ、方向が全部決まってしまいます。

つまり、直角三角形なら、斜辺と他の一辺の長さが決まっただけで合同であると言うことができるのです。

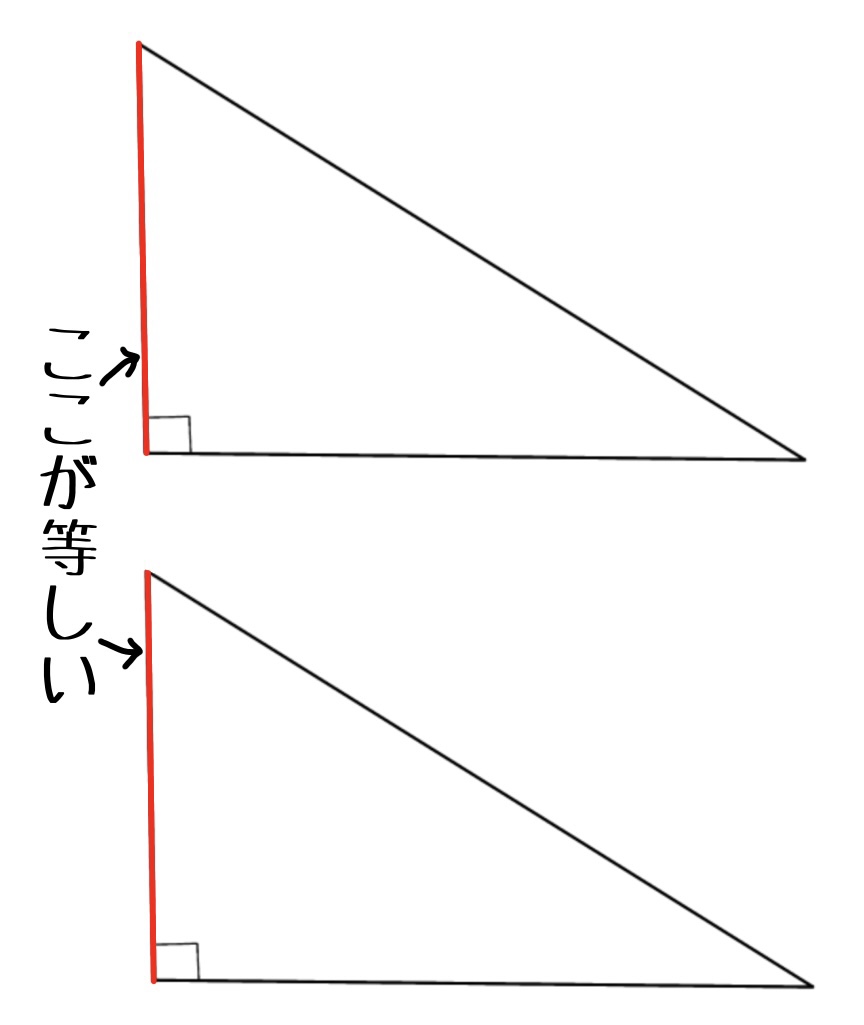
図のように、斜辺ではない１つの辺が等しかったとしましょう。

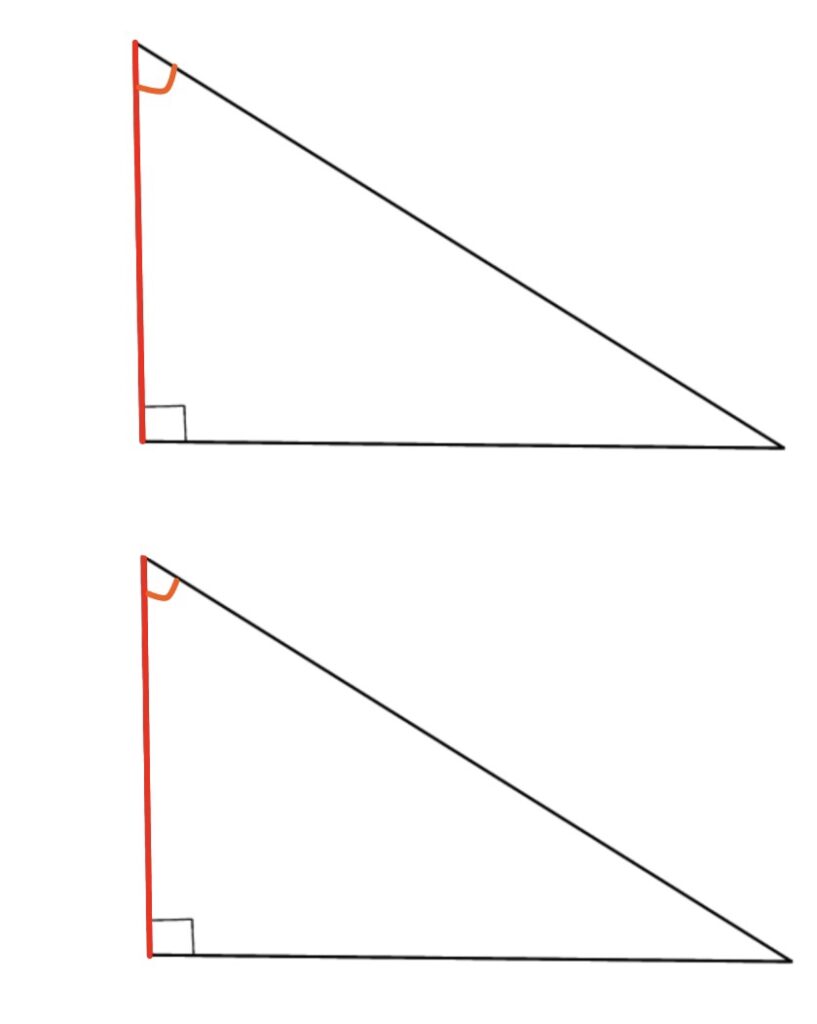
「斜辺と１つの鋭角がそれぞれ等しい」の合同条件では、１つの角が等しいことが必要になります。それを図でオレンジ色で示した角とします。

そうするとこれは「１組の辺とその両端の角がそれぞれ等しい」で合同だと分かります。

つまり、直角三角形の合同条件を使う必要がないのです。

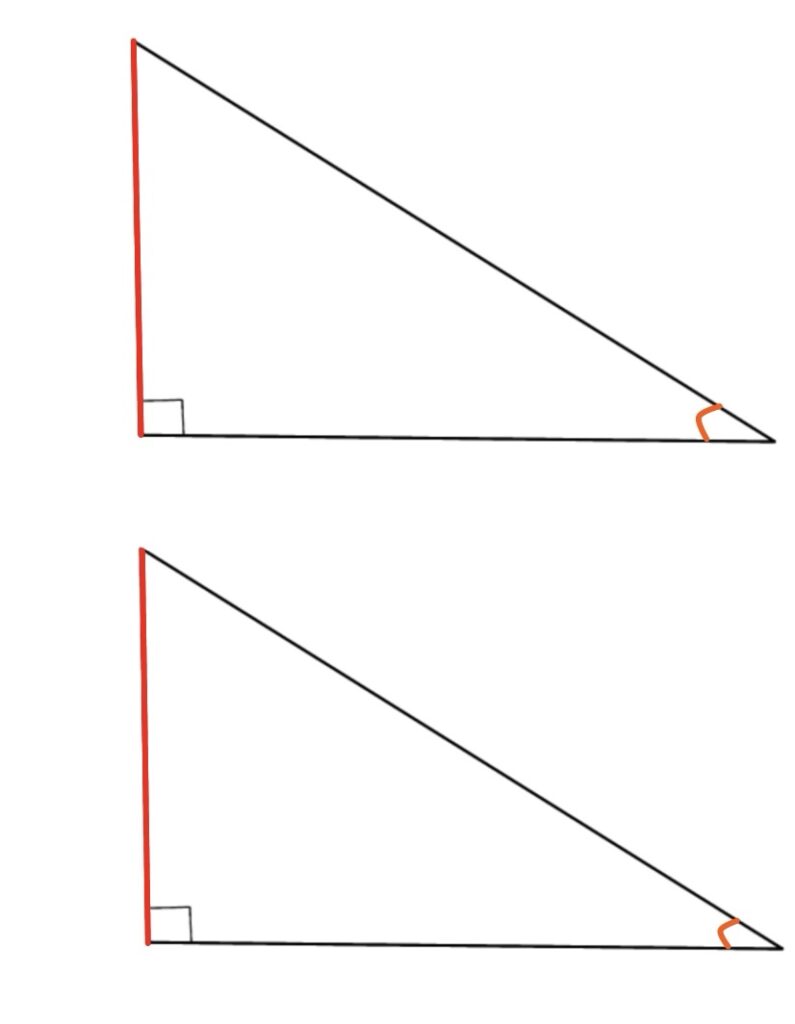
別の角が等しいことが分かったとしましょう。

この場合でも、２つの角が等しいなら三角形の内角の和でもう一つの角も等しいことが分かります。

だから結局１組の辺とその両端の角がそれぞれ等しい」で合同だと分かるのです。

それなら直角三角形の合同条件を使う必要がないですよね。

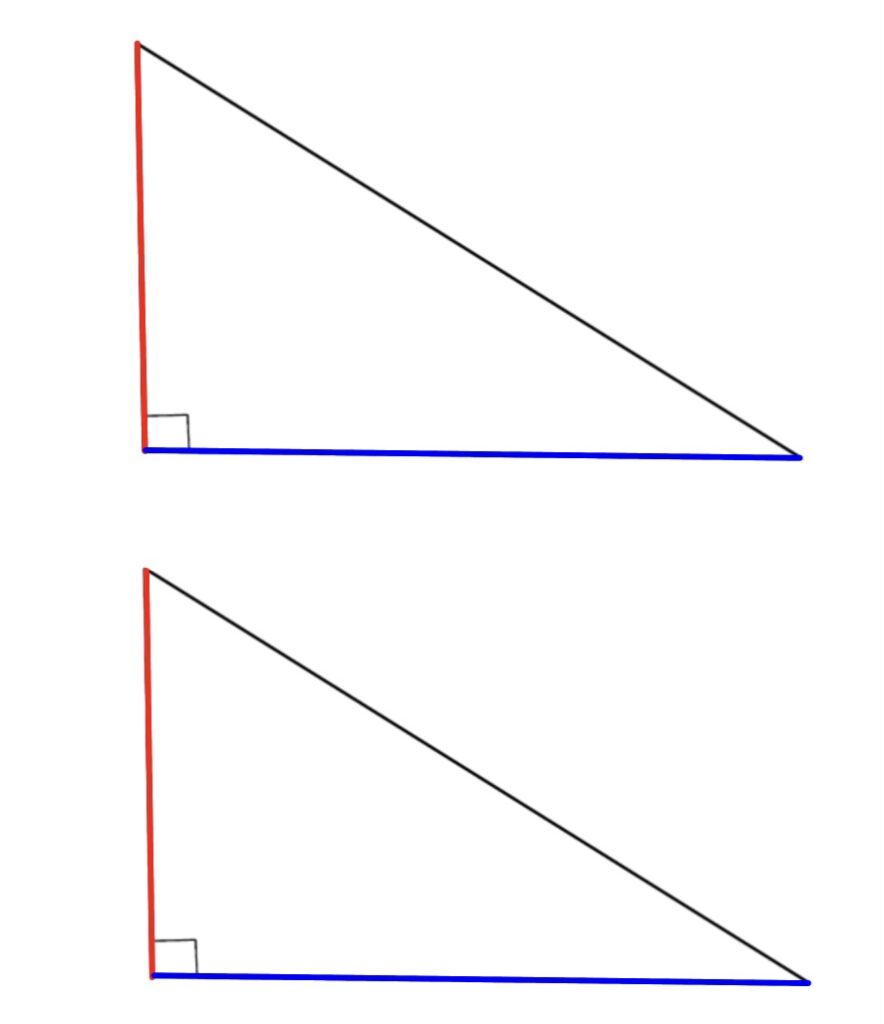
斜辺以外の一辺と他の一辺が等しかった時のことも考えましょう。

図をご覧いただいても分かるように、斜辺以外の辺が等しいということは、その間の角は直角で等しいので、「２組の辺とその間の角がそれぞれ等しい」で合同だと証明できるのです。

それなら別に「斜辺と他の一辺がそれぞれ等しい」を使う必要はないですよね。