一次関数の基本用語、基礎知識は大丈夫ですか?もし「あやしいな」と思うときは、こちらの記事をご覧下さい。
この記事を見ている最中でも「あれ?分からないな」と思った時にはご覧下さい。
何事も基本が一番大切ですから!この記事内でも振り返りますけど。
グラフでの基本事項確認

一次関数のグラフの描き方・式の求め方
グラフを描くときの考え方
\(y=2x+1\)で説明します
\(y=2x+1\)の\(x\)に、-3~3までの値を入れて表を作ると以下のようになります。
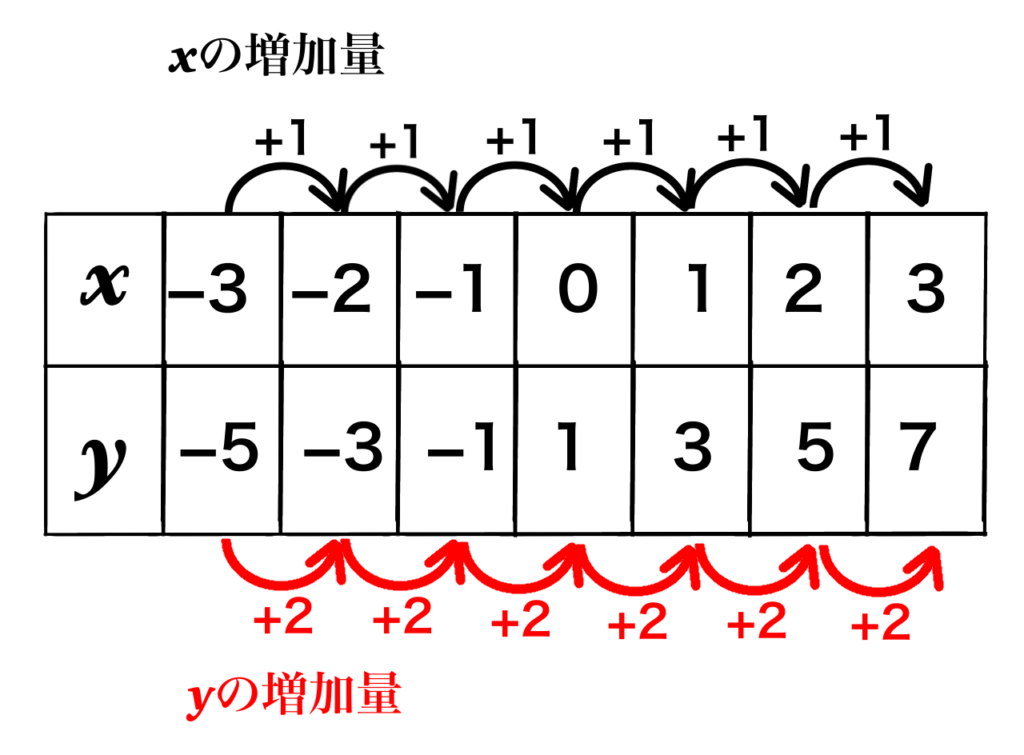
ご覧のように、\(x\)が1つ増えると\(y\)が2つ増えています。これをグラフにしましょう。
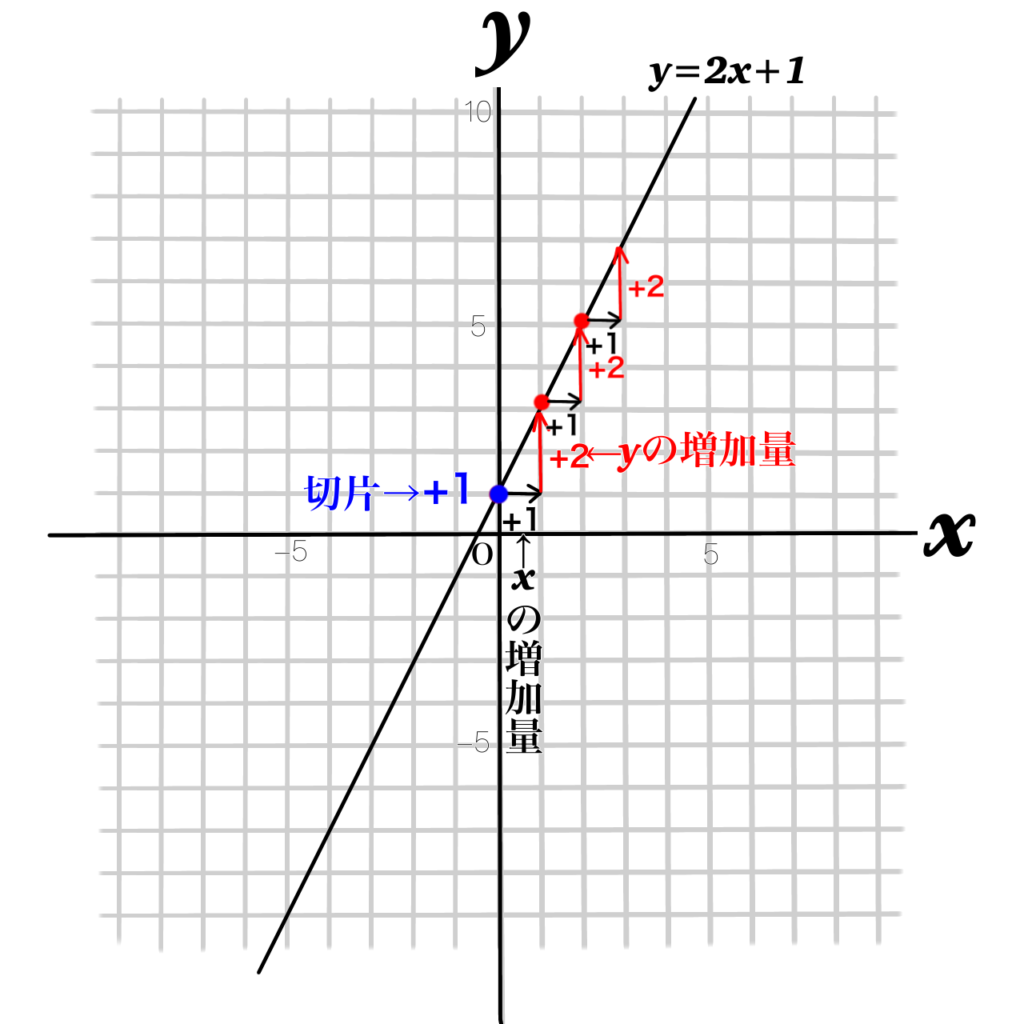
\(x\)が1つ増えると\(y\)が2つ増える様子はグラフではここに表れます。これが式の中の傾きになっています。
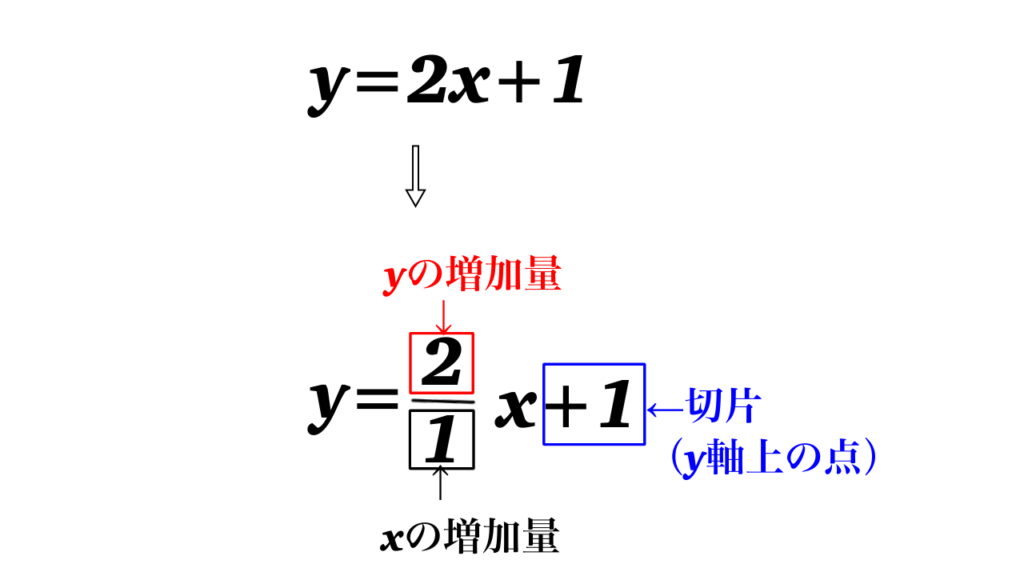
傾きは変化の割合の式 \(\dfrac{yの増加量}{xの増加量}\)を使って分数にすると、
分母⇒\(x\)の方(横)に進む数
分子⇒\(y\)の方(縦)に進む数
このように考えると分数のときでもグラフが書きやすくなるのでオススメです。実際の問題でやってみましょう!

…しなくていいけど💧
式からグラフを描く
手順は以下の通りです。
| ①式の切片を\(y\)軸上にとる |
| ②\(傾き=変化の割合=\dfrac{yの増加量}{xの増加量}\)を使って点を打つ |
| ③②の行程を何回か繰り返して、点の上を通るように直線を描く |
さて、やってみましょう!
例題1 \(y=x-4\)
①式の切片-4を\(y\)軸上にとります
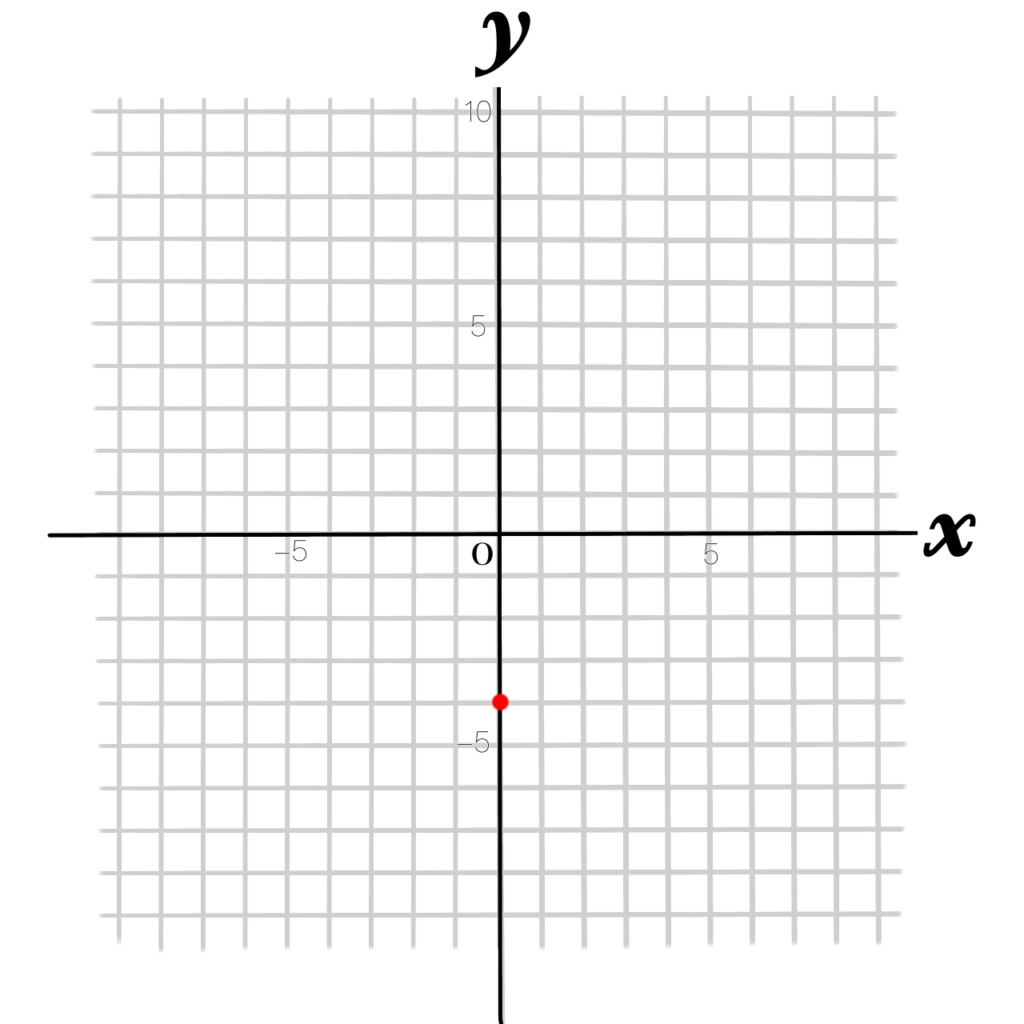
②傾きが1なので、分数にすると\(\dfrac{1}{1}\)です。
\(傾き=変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{1}{1}\)
分母=\(x\)の増加量=1
分子=\(y\)の増加量=1
つまり
分母⇒\(x\)が1つ増えると
分子⇒\(y\)も1つ増えます。
これを1セットとして点を打っていきます。
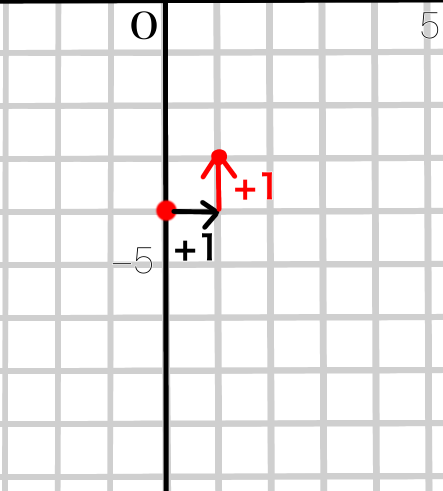
③②と同じようにして何個か点を打ちます。(直線がずれないようにするため)
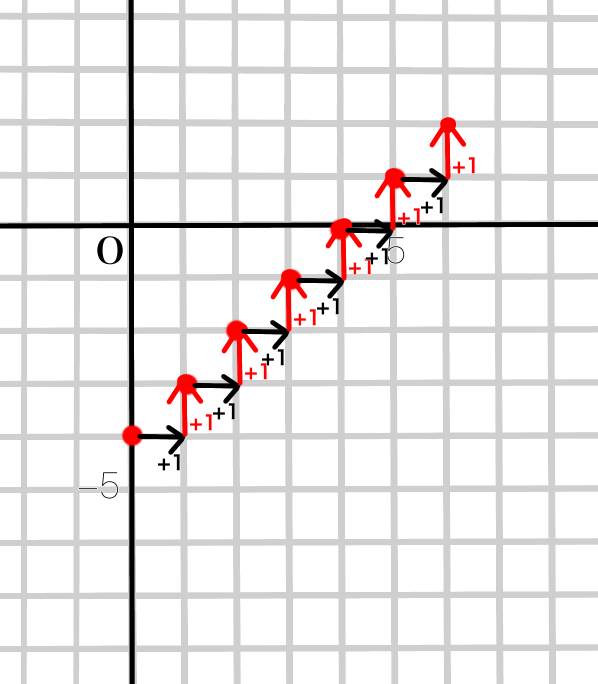
④直線でつないで完成です!
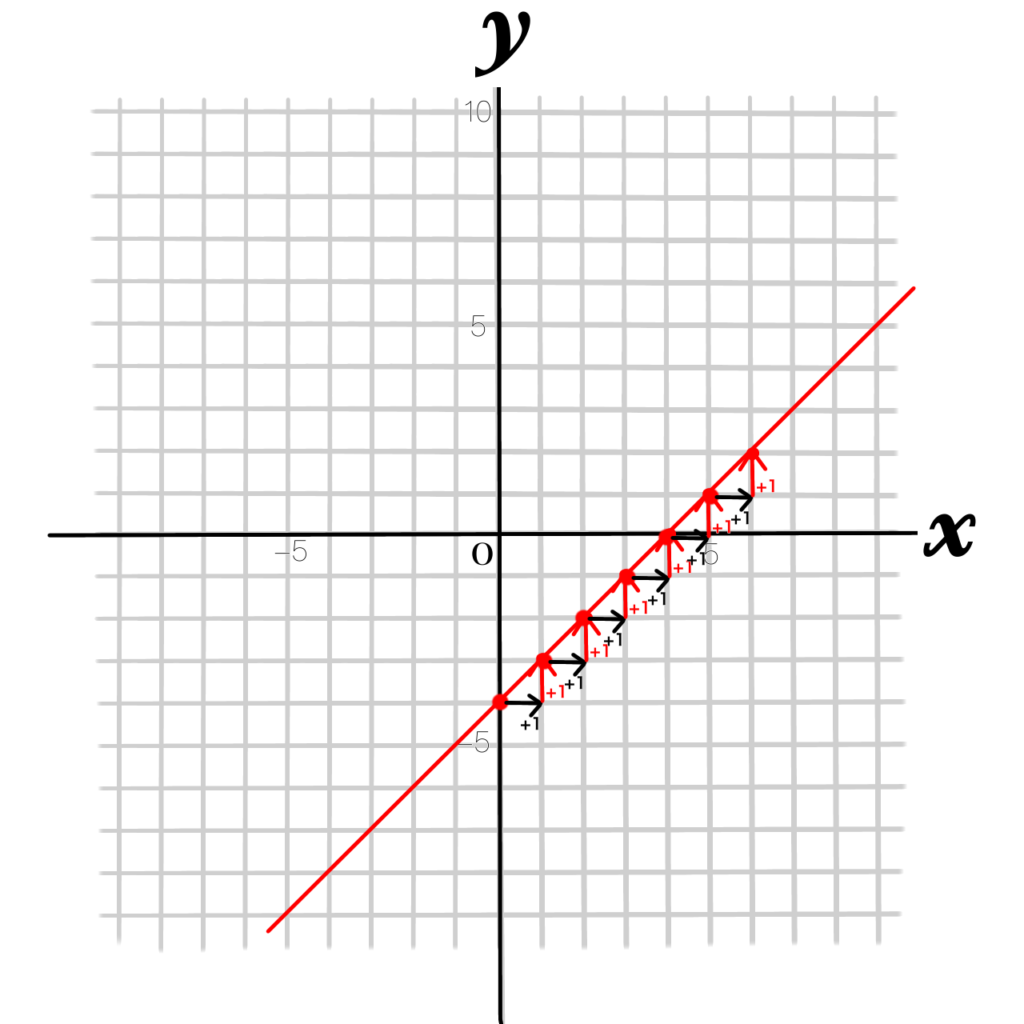
実際、2点あれば直線は書けます。でも、間隔が狭いとずれやすいので、何個か点を打って結ぶと良いと思います。
例題2 \(y=-3x+2\)
①式の切片+2を\(y\)軸上にとります
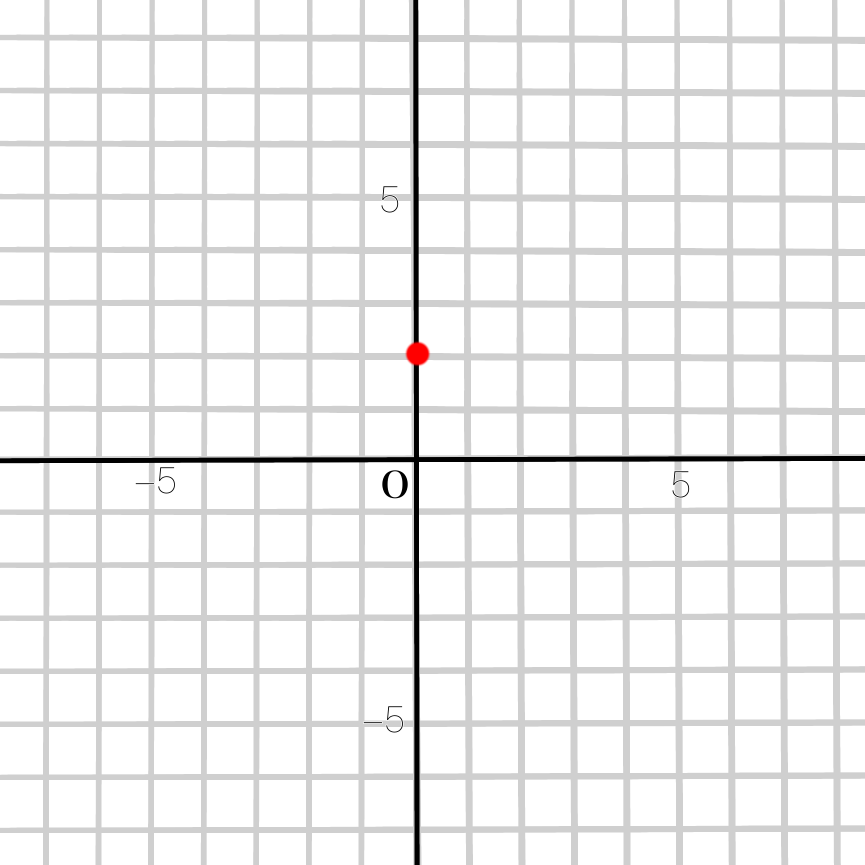
②傾きが-3なので、分数にすると\(\dfrac{-3}{1}\)。
\(傾き=変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{-3}{1}\)
分母⇒\(x\)が1つ増えると
分子⇒\(y\)は3つ減ります。
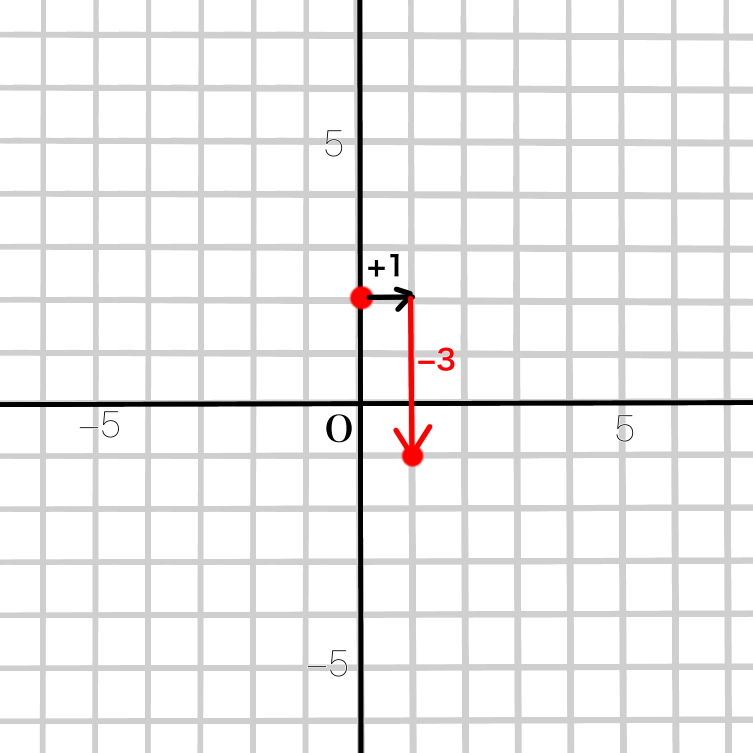
③②と同じようにして何個か点を打ちます。(直線がずれないようにするため)
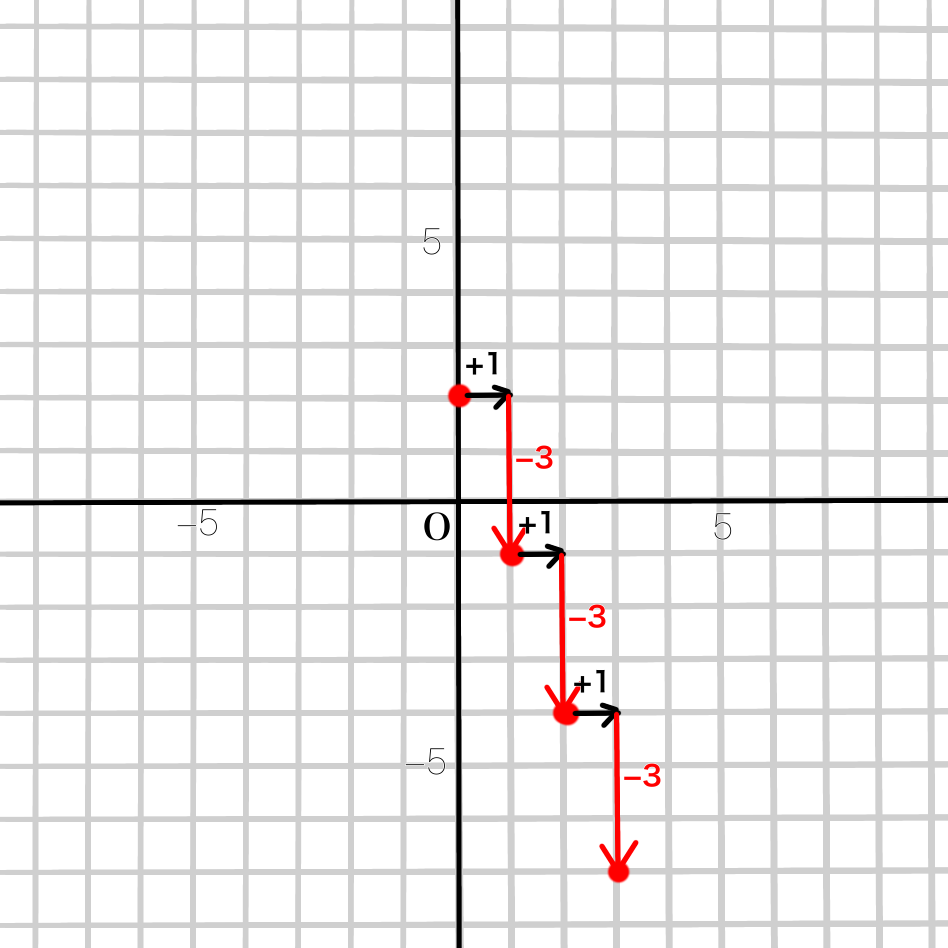
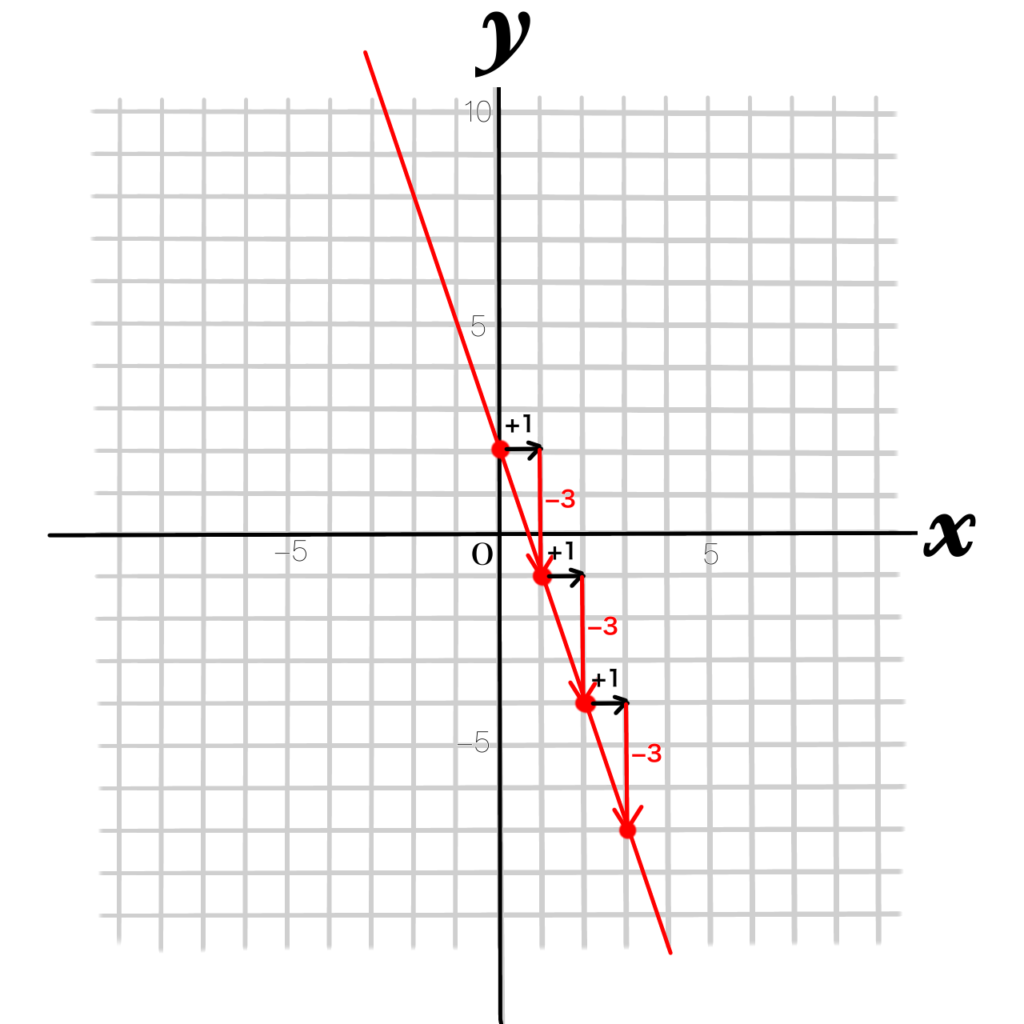
④直線でつないで完成です!
例題3 \(y=\dfrac{5}{4}x-7\)
①式の切片-7を\(y\)軸上にとります
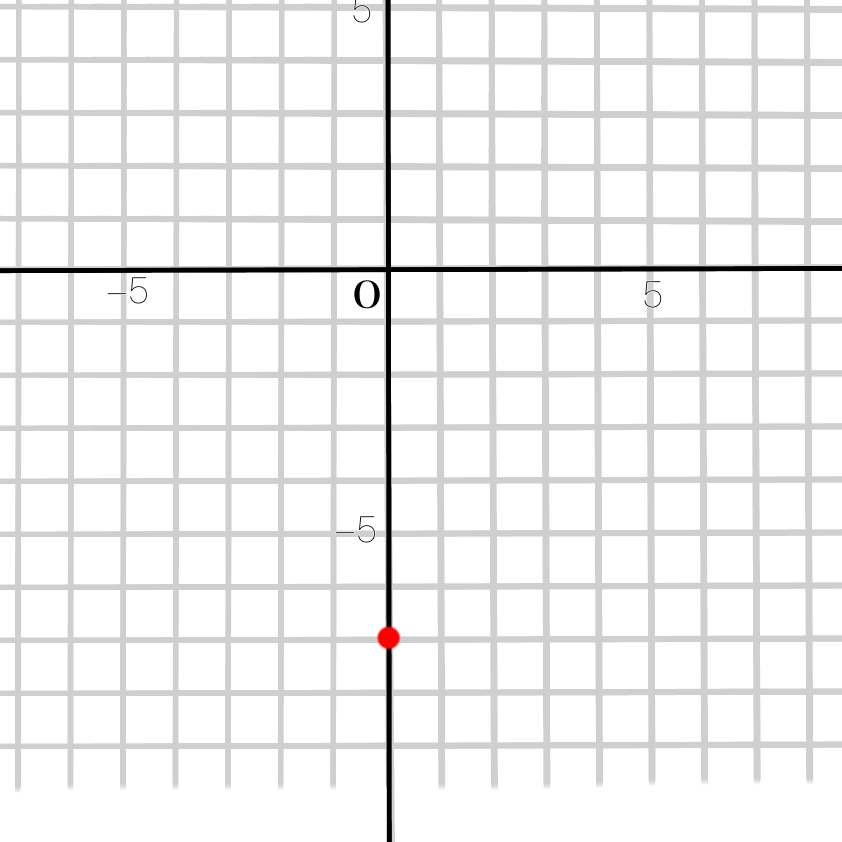
②傾きが\(\dfrac{5}{4}\)なので、
分母⇒\(x\)が4つ増えると
分子⇒\(y\)は5つ増えます。
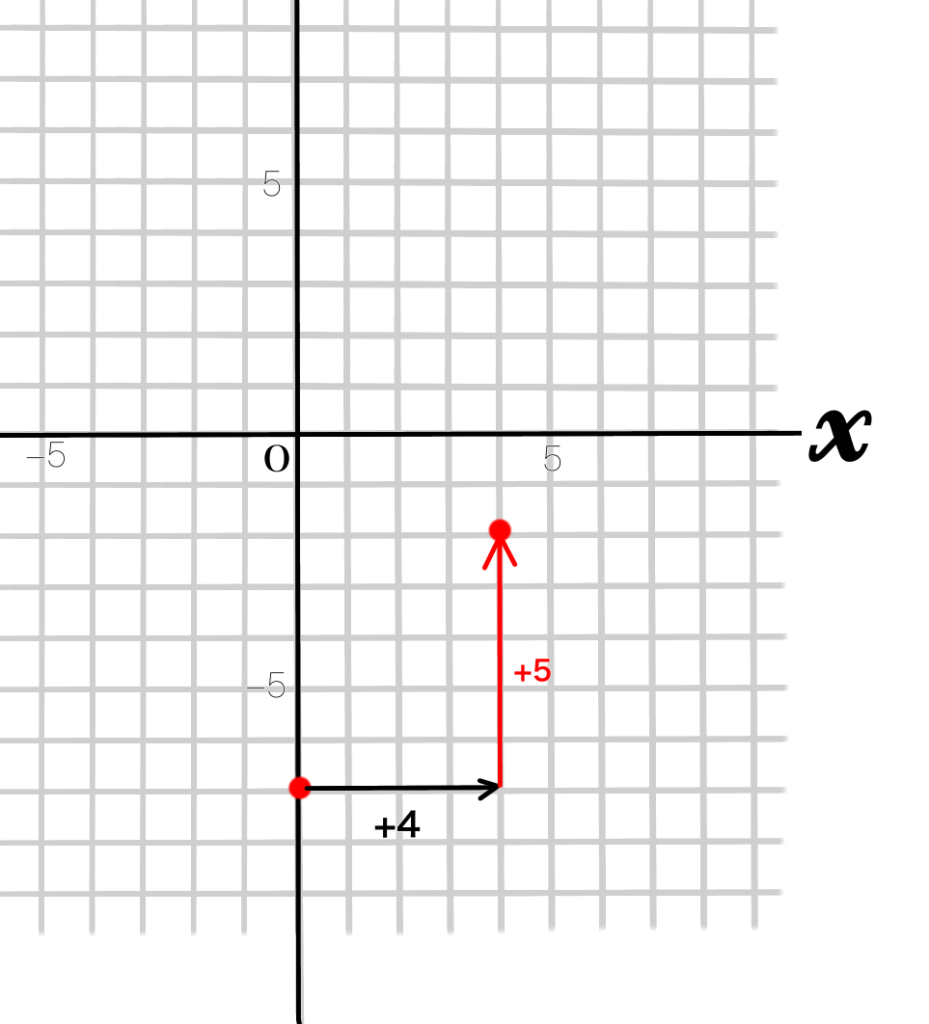
③②と同じようにして何個か点を打ちます。(直線がずれないようにするため)
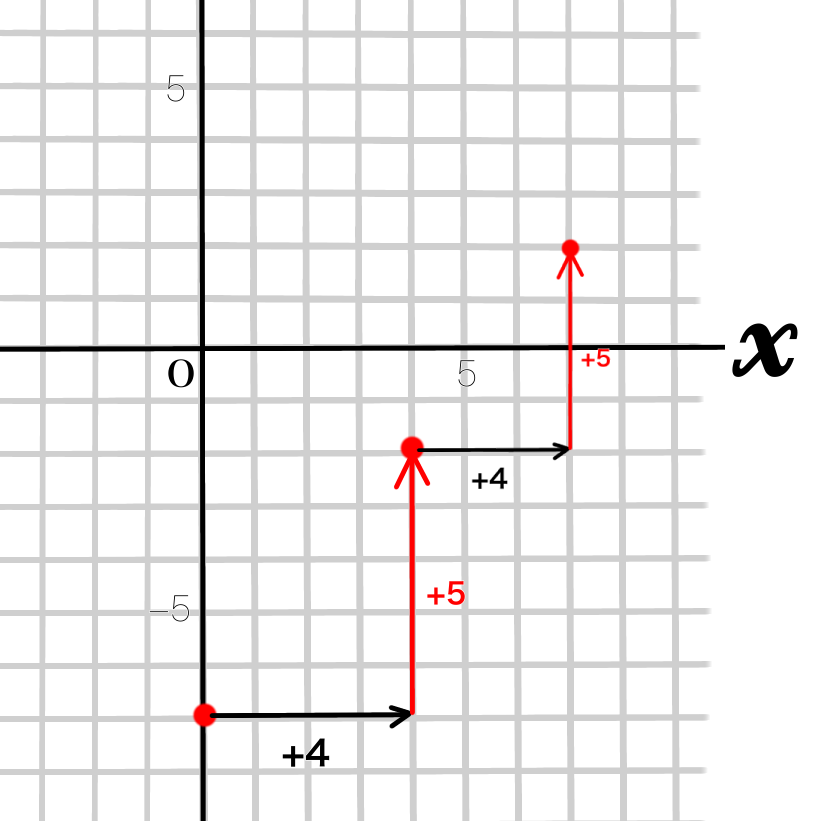
④直線でつないで完成です!
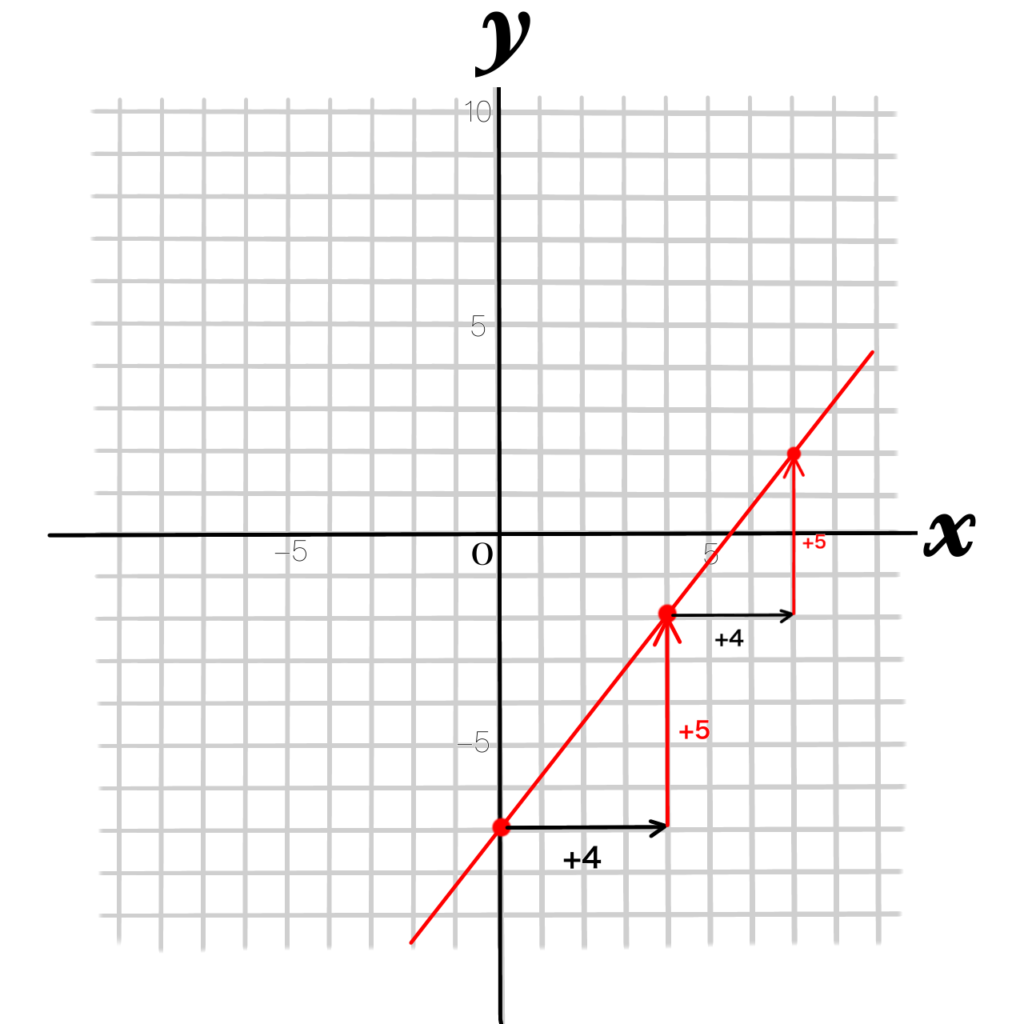
グラフを読み取って式にしてみよう!
グラフが書ければ、読み取りだってできます!
| ①切片(\(y\)軸と交わっている点)を読み取る⇒\(b\)の値 |
| ②切片以外の座標が交わっている点を見つける。そして、 \(x\)がいくつ増えて、\(y\)がいくつ増えたか? を読み取って傾き\(a\)を出します。 |
| ③読み取った数を\(y=ax+b\)の\(a\)と\(b\)のところに入れれば完成です! |
なんとなく手順を書いてみると分かりづらいですね。
実際にやってみましょう!
例題1
例題1 このグラフの式を求めなさい
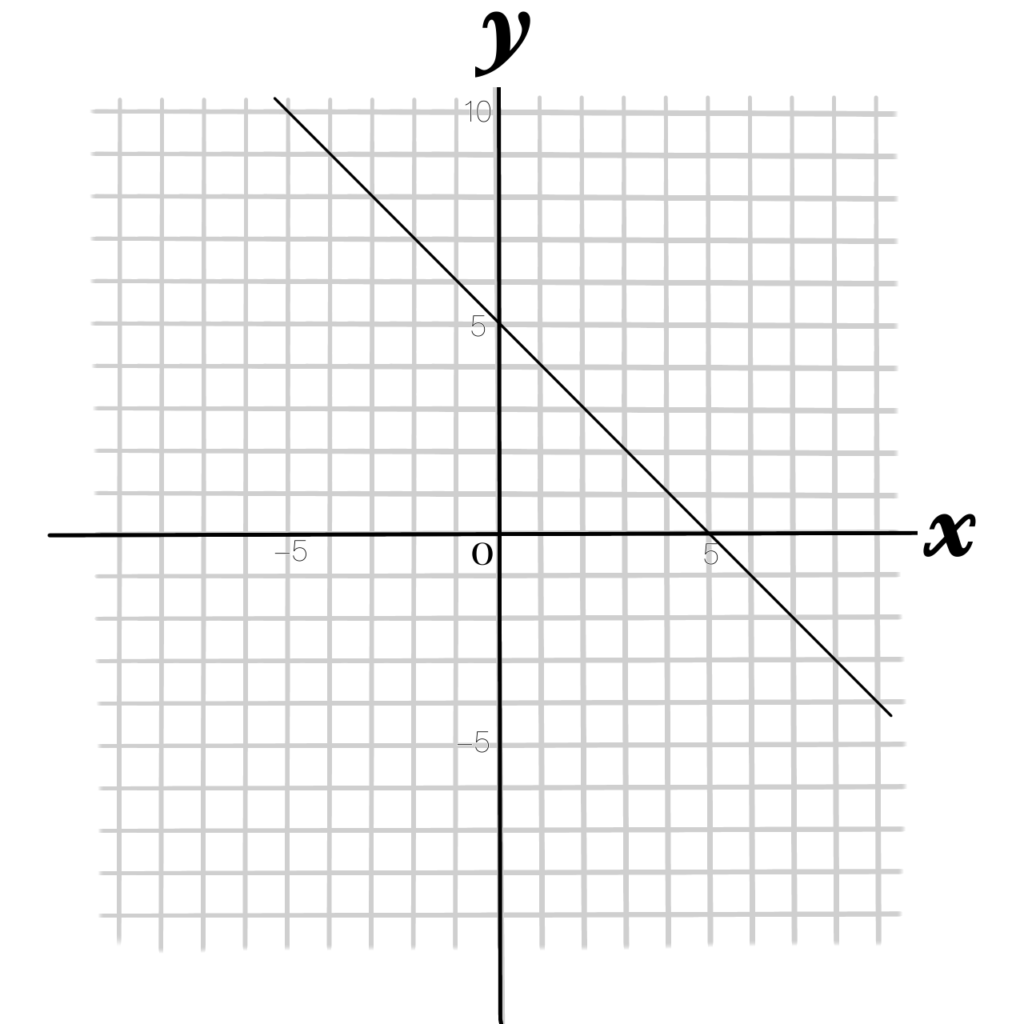
①まず切片を読み取ります。
\(y\)軸上の点は、「5」になっています。切片\(b\)は5です。
②グラフを拡大しましょう!
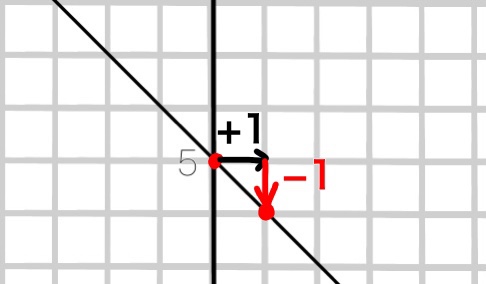
切片5のところから、\(x\)が1増えると、\(y\)は1減っています。つまりこういうことです。
\(x\)の増加量…+1
\(y\)の増加量…-1
この値を
\(傾き=変化の割合=\dfrac{yの増加量}{xの増加量}\)
これに入れると、
\(\dfrac{-1}{1}=-1\)となります。
よって、傾き\(a\)は-1です。
③\(a\)と\(b\)の数を\(y=ax+b\)に入れます。
\(y=-1x+5\) …ですが、文字の前の1は省略しますので答えは
\(y=-x+5\)となります!
答え \(y=-x+5\)
例題2
例題2 このグラフの式を求めなさい
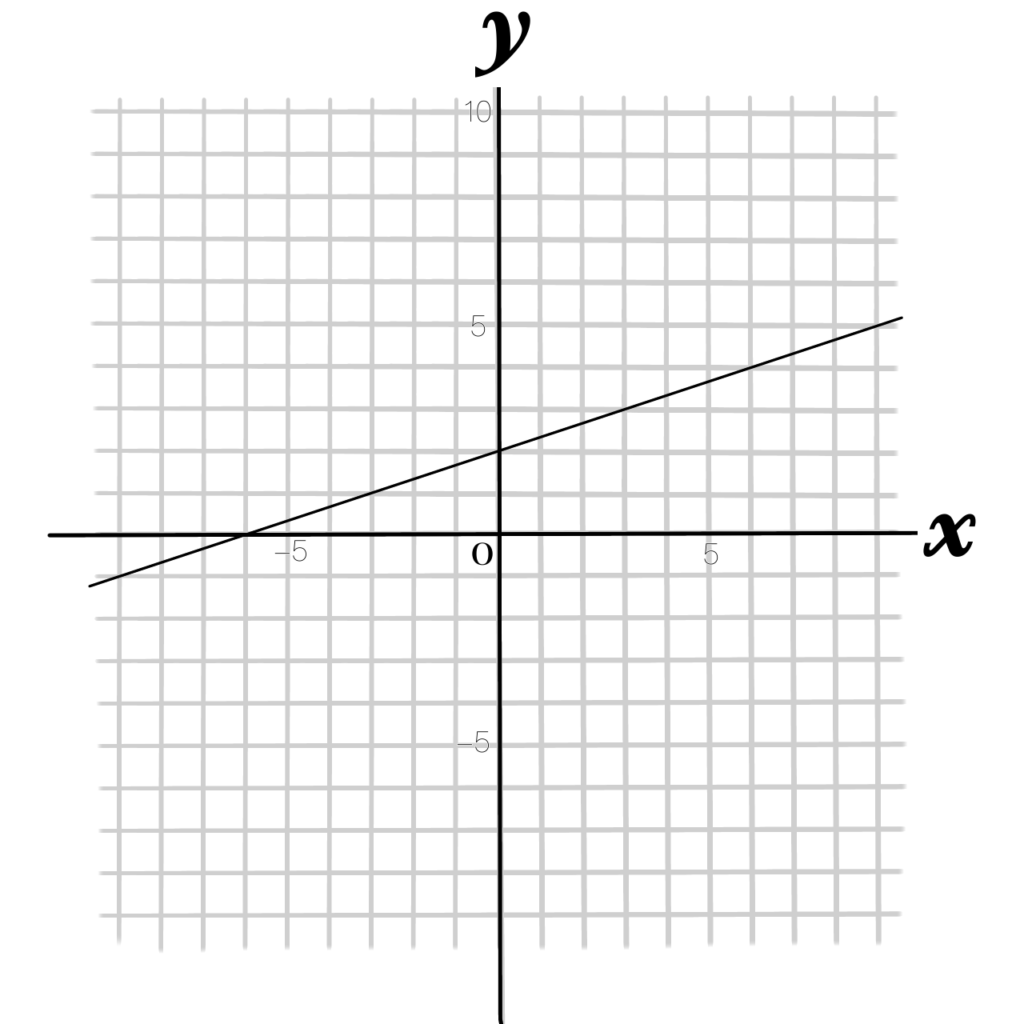
①\(y\)軸上の点は、「2」になっています。切片\(b\)は2です。
②グラフを拡大しましょう!
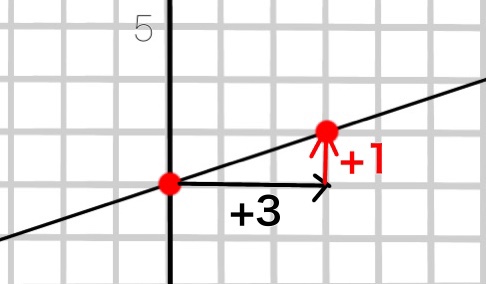
切片2のところから、\(x\)が3増えると、\(y\)は1増えています。
\(x\)の増加量⇒3
\(y\)の増加量⇒1
\(変化の割合=\dfrac{yの増加量}{xの増加量}\)
これに当てはめると、
\(\dfrac{1}{3}\)
傾き\(a\)は\(\dfrac{1}{3}\)となります。
③傾き\(a=\dfrac{1}{3}\)、切片\(b=2\)を\(y=ax+b\)に入れると、
\(y=\dfrac{1}{3}x+2\)
となります!
答え \(y=\dfrac{1}{3}x+2\)

例題3
例題3 このグラフの式を求めなさい
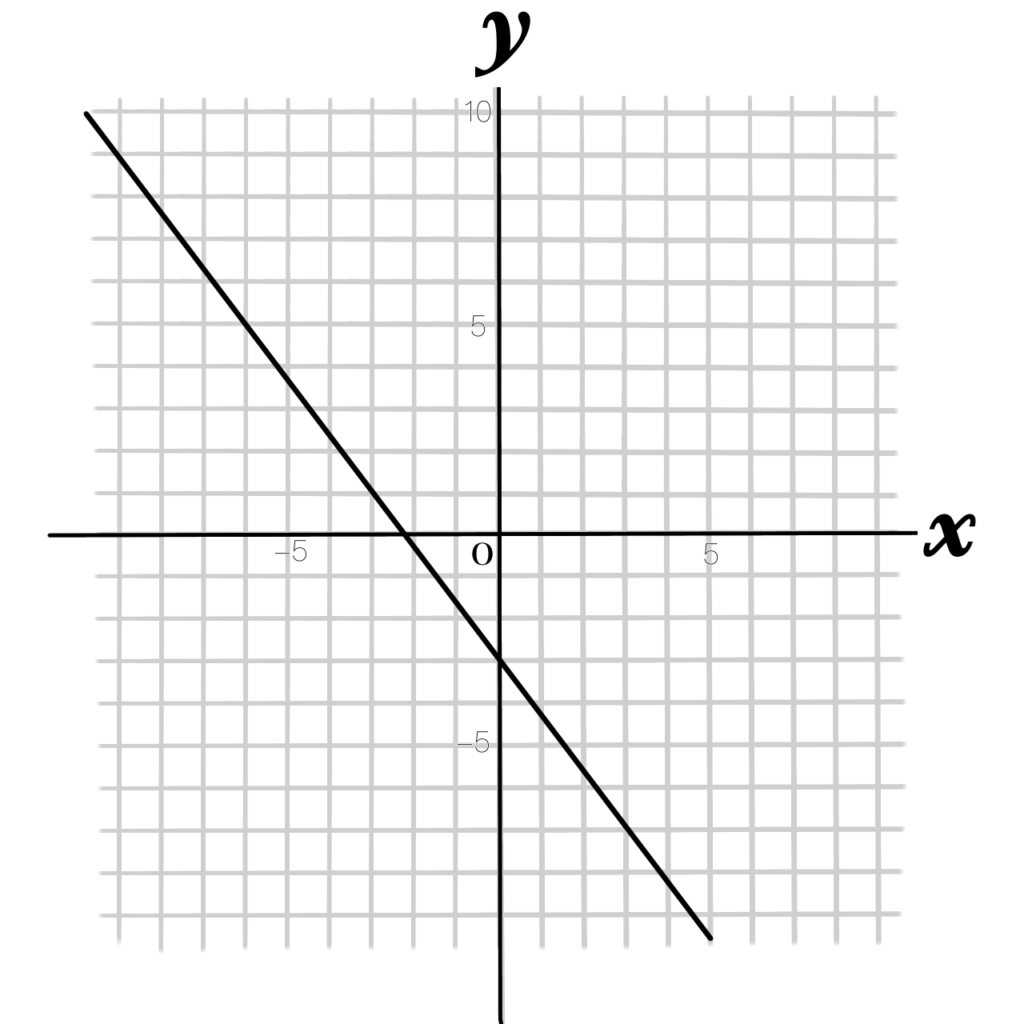
①まず切片\(b\)を読み取ります。
\(y\)軸上は「-3」を通っていますので、切片\(b\)は-3です。
②次に傾きですが、まず拡大してみます。
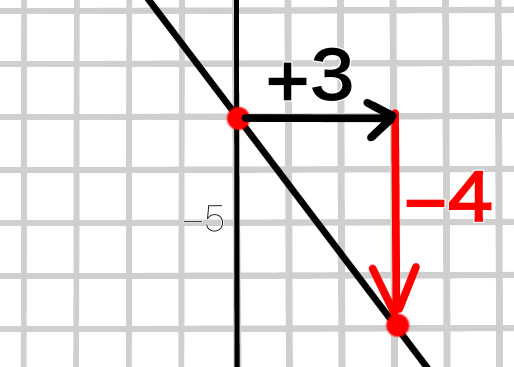
切片-3のところから、\(x\)が3増えると、\(y\)は4減っています。
\(xの増加量=3\)
\(yの増加量=-4\)
これを変化の割合の式に当てはめます。
\(変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{-4}{3}\)
傾き\(a\)は\(-\dfrac{4}{3}\)です。
③傾き\(a=-\dfrac{4}{3}\)、切片\(b=-3\)を\(y=ax+b\)に入れると、
\(y=-\dfrac{4}{3}x-3\)
答え \(y=-\dfrac{4}{3}x-3\)
こんな感じで読み取れますので、やってみて下さいね!
ここまでで、グラフの読み取り方と描き方の説明は終了です!……っと?

ちょっと待ったぁぁ!!!

どうしたでおじゃるか?

\(x=3\)とか\(y=-1\)のグラフを描けって問題出てきたんだけど。どうすればいいの?

おお!忘れておった。説明するでおじゃる
\(x=\)数字 \(y=\)数字のグラフ
例題1 \(x=3\)
この式は、\(y\)が入っていません。
ですから、\(y\)の値に関係なく、\(x\)は3の値をとり続ける、という意味です。
ですので、グラフの描き方は図のようになります。
①点を打つ
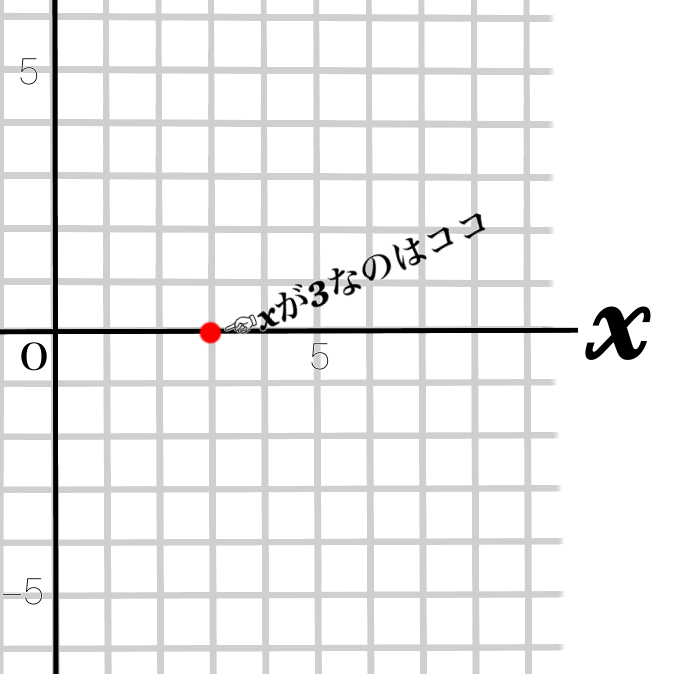
②点を打つ!
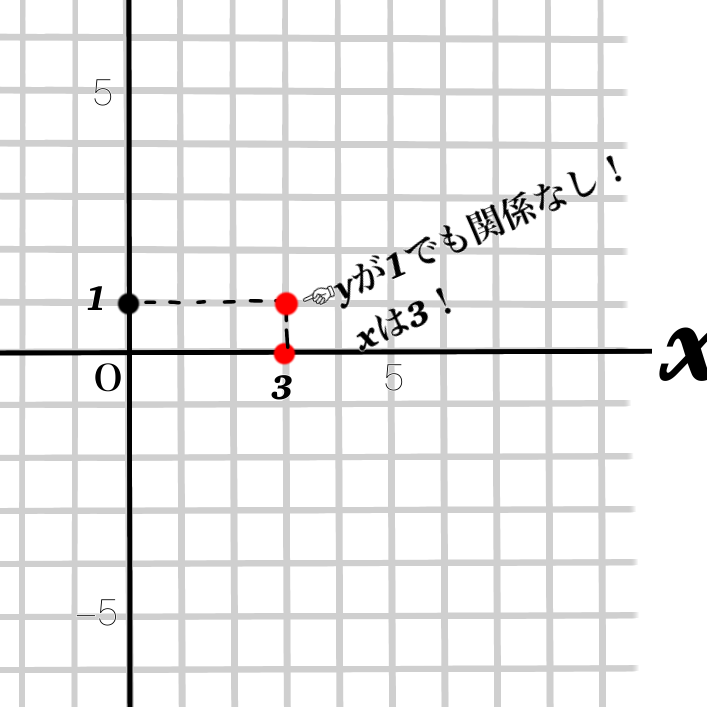
③点を打つ点を打つ点を打つ!!
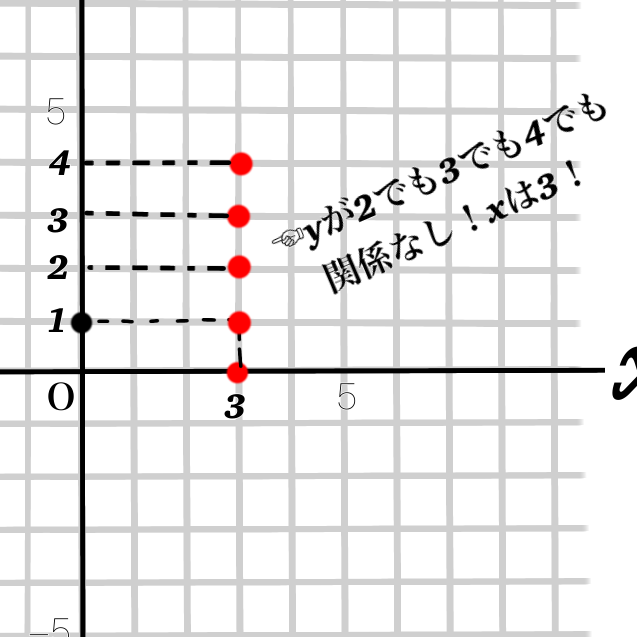
④線を描く
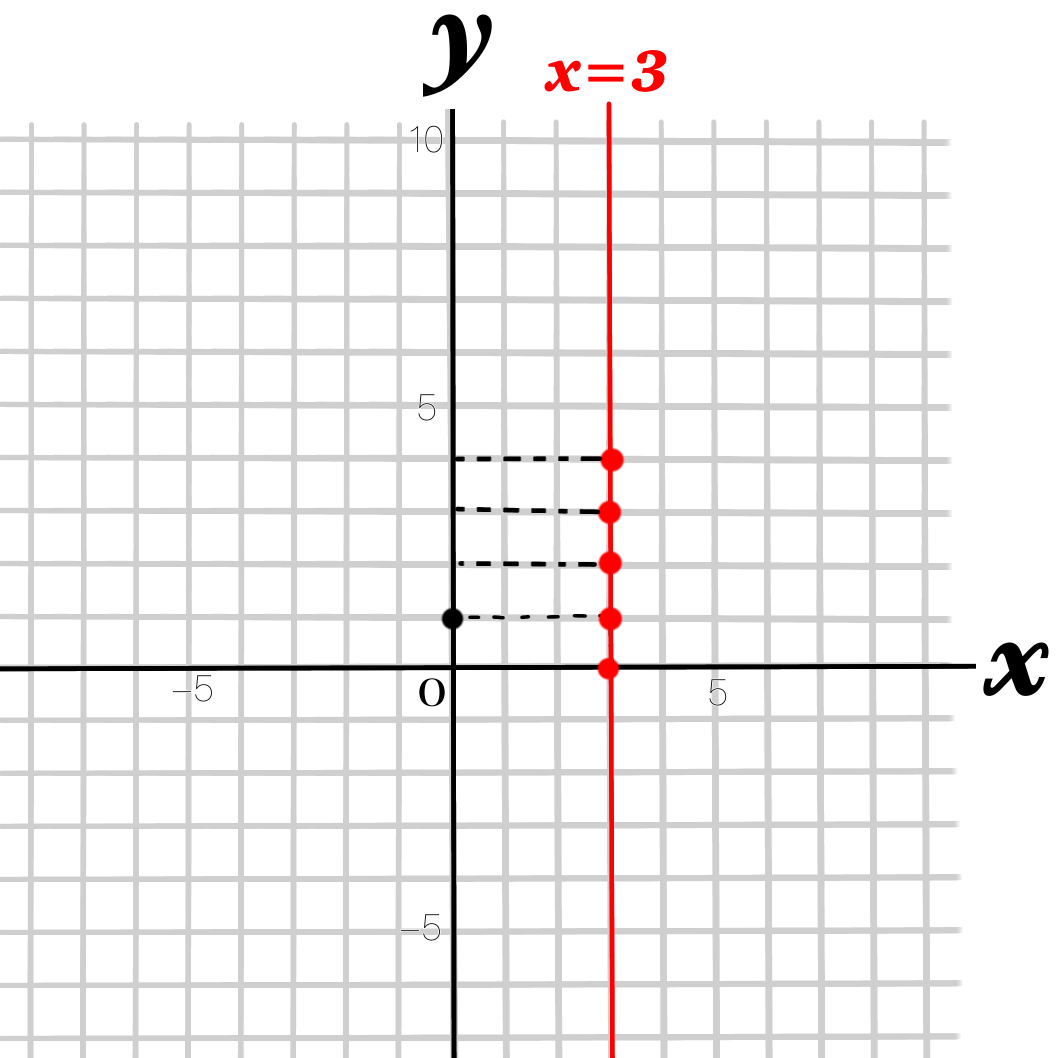
\(x=数字\)の場合は、\(y\)軸に平行なグラフになります。
例題5 \(y=-1\)
この式は、\(x\)が入っていません。
ですから、\(x\)の値に関係なく、\(y\)は-1の値をとり続ける、という意味です。
ですので、グラフの描き方は図のようになります。
①点を打つ
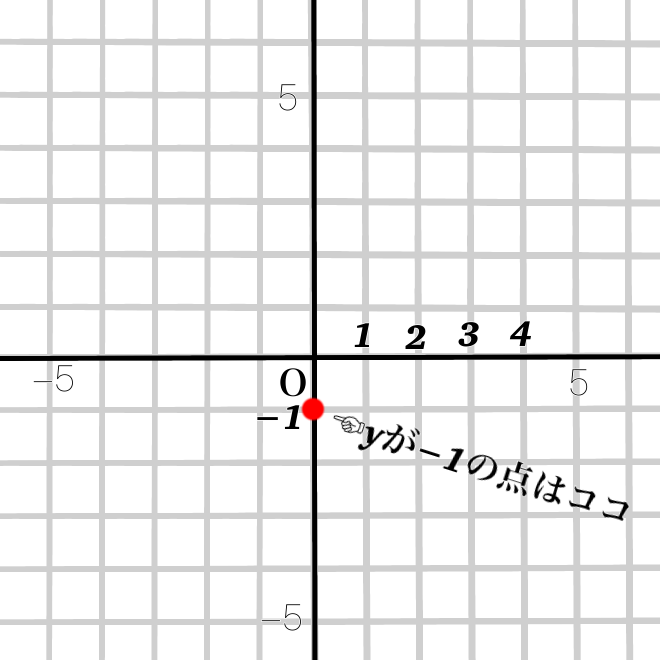
②点を打つ!
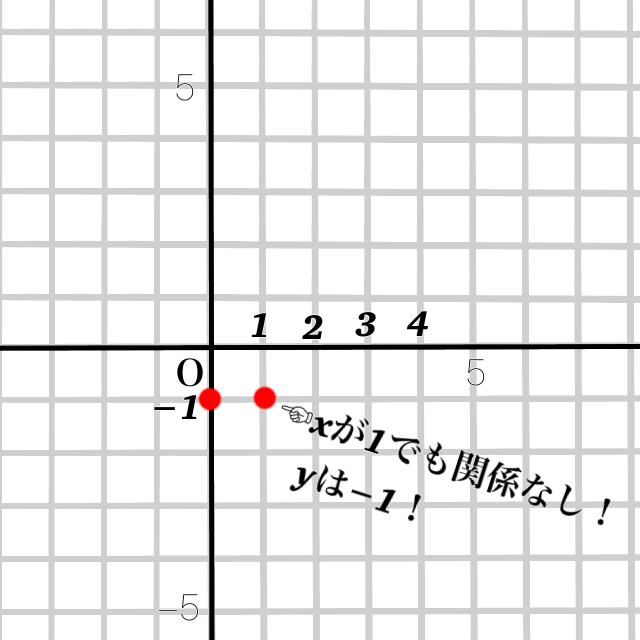
③点を打つ点を打つ!!
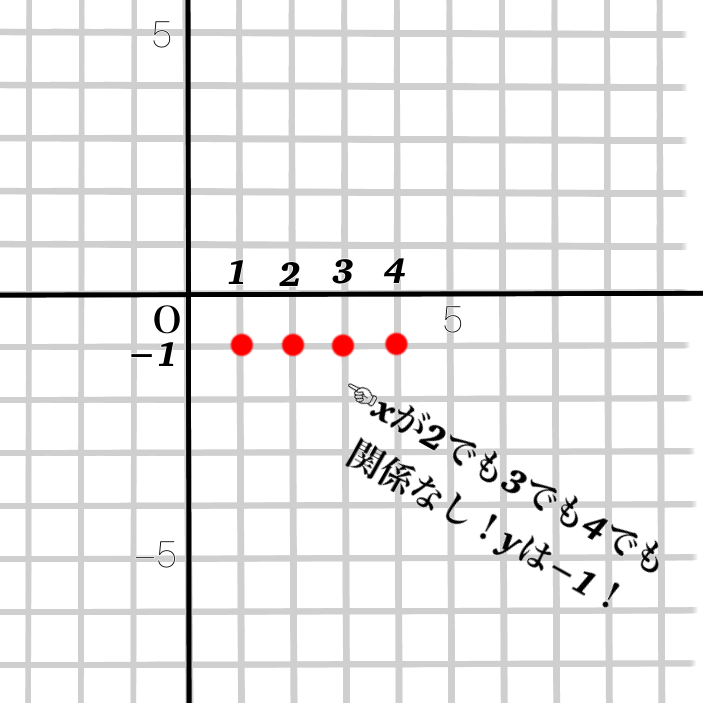
④線を描く
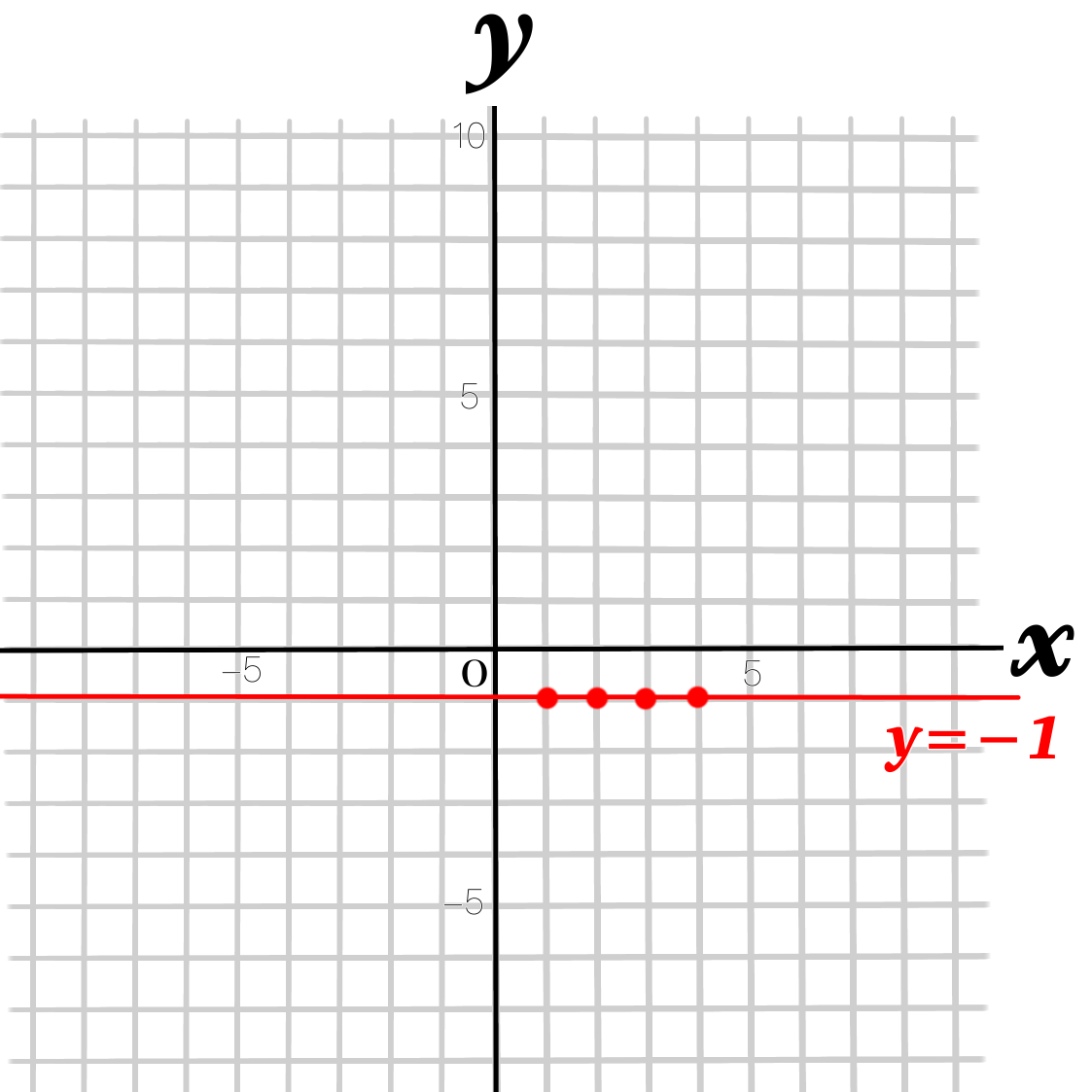
\(y=数字\)の場合は、\(x\)軸に平行なグラフになります。

わかったでおじゃるか?

今度こそグラフの読み取り方と描き方の説明は終了です!
次の記事では問題文から式を求める方法を解説していきます!



コメント