一次関数ってなに?



全部違います!!(笑)
簡単に言うと
| 簡単な説明 | 例 | |
| 式の形 | \(y=ax+b\) (\(a\)と\(b\)に数字が入る) | \(a=3\) , \(b=-2\)のとき \(y=3x-2\) |
| 言葉の意味 | \(y=\)の右側(右辺) が一次式になる関数 | \(y=3x-2\) は右辺が一次式。 だから一次関数。 |
| グラフ | 直線になる | 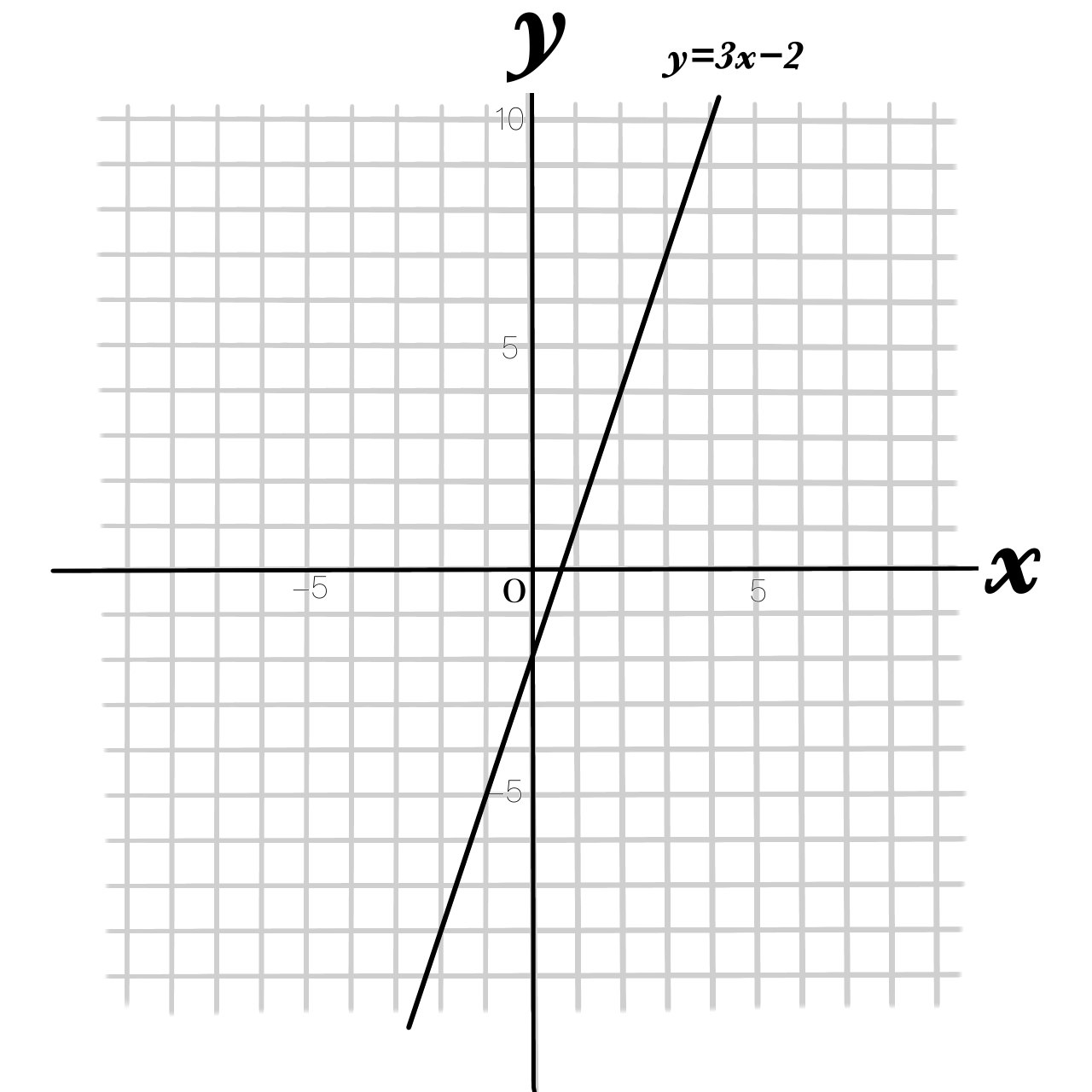 |
ちょっと詳しく説明
一次式と一次関数
中学2年生の序盤で、「一次式」とか「二次式」という言葉を習ったと思います。
1つの項(単項式)に文字が1つあれば「次数1」、文字が2つあれば「次数2」でした。
\(3a\)⇐\(a\)という文字が1つあるから「次数1」
\(2xy\)⇐\(x\)と\(y\)で2つ文字があるから「次数2」
\(4x^2\)⇐\(x^2\)は、\(x\)が2個を意味するので「次数2」
+やーで繋がれた式(多項式)の場合
\(2x^2-3x+1\)
この場合は、\(2x^2\)が次数2、\(-3x\)が次数1、\(+1\)が次数0なので、一番多い次数が代表になって、この式は「2次式」という言い方をしました。
ということは、一次式は次のようなものになります。
\(2x+1\) ⇐文字が1つの項「\(2x\)」と数字「\(+1\)」
\(3x\) ⇐文字が1つの項「\(3x\)」
\(\dfrac{1}{2}x+\dfrac{2}{3}\) ⇐文字が1つの項「\(\dfrac{1}{2}x\)」と数字「\(+\dfrac{2}{3}\)」
このように、「文字が1つの項+数字」または、文字が1つの項だけの式を「一次式」と言います。
そして、「一次関数」は、左辺(=の左側)を\(y=\)としたとき、右辺(=の右側)が一次式になる式を「一次式の関数」=「一次関数」と言うわけです。

つまり、
\(y=2x+1\)、\(y=\dfrac{1}{2}x+\dfrac{2}{3}\)のような式を一次関数と言い、数字部分に\(a\)と\(b\)を当てはめて
\(y=ax+b\)
としたのが、一次関数の一般的な形になります。
ちなみに、\(y=3x\)のような、中学1年生で学習した比例の式も、\(y=ax+b\)の\(a\)が3、\(b\)が0の一次関数と考えることができます。
ただし、同じ中1で学習した反比例\(y=\dfrac{6}{x}\)のような、\(x\)が分母にくる関数は一次関数ではありませんので注意してください。
表と座標とグラフ&用語
式から表を作ってグラフを書くまで
\(y=2x+1\)
この式の\(x\)に色々な数字を当てはめてみましょう。
| 式 | \(x\)の値 | 計算 | \(y\)の値 |
| \(y=2x+1\) | 0 | \(y=2\times 0+1=1\) | 1 |
| \(y=2x+1\) | 1 | \(y=2\times 1+1=3\) | 3 |
| \(y=2x+1\) | 2 | \(y=2\times 2+1=5\) | 5 |
| \(y=2x+1\) | 3 | \(y=2\times 3+1=7\) | 7 |
| \(y=2x+1\) | -1 | \(y=2\times \left( -1\right) +1=-1\) | -1 |
| \(y=2x+1\) | -2 | \(y=2\times \left( -2\right) +1=-3\) | -3 |
| \(y=2x+1\) | -3 | \(y=2\times \left( -3\right) +1=-5\) | -5 |
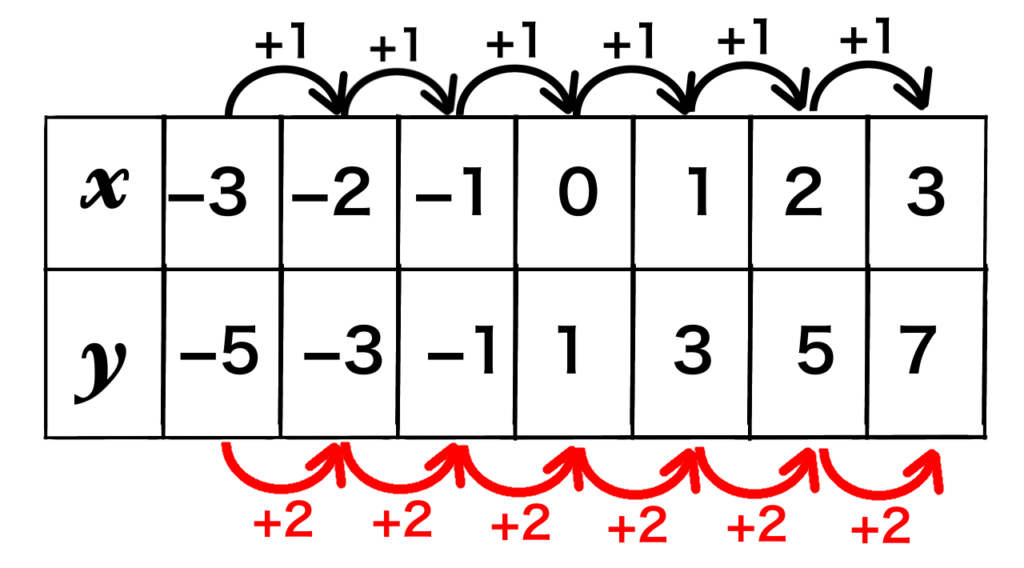
これを表にまとめます。
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | -5 | -3 | -1 | 1 | 3 | 5 | 7 |
| 座標 ( \(x\) , \(y\) ) | (-3,-5) | (-2,-3) | (-1,-1) | (0,1) | (1,3) | (2,5) | (3,7) |
グラフに座標を書いていきます。
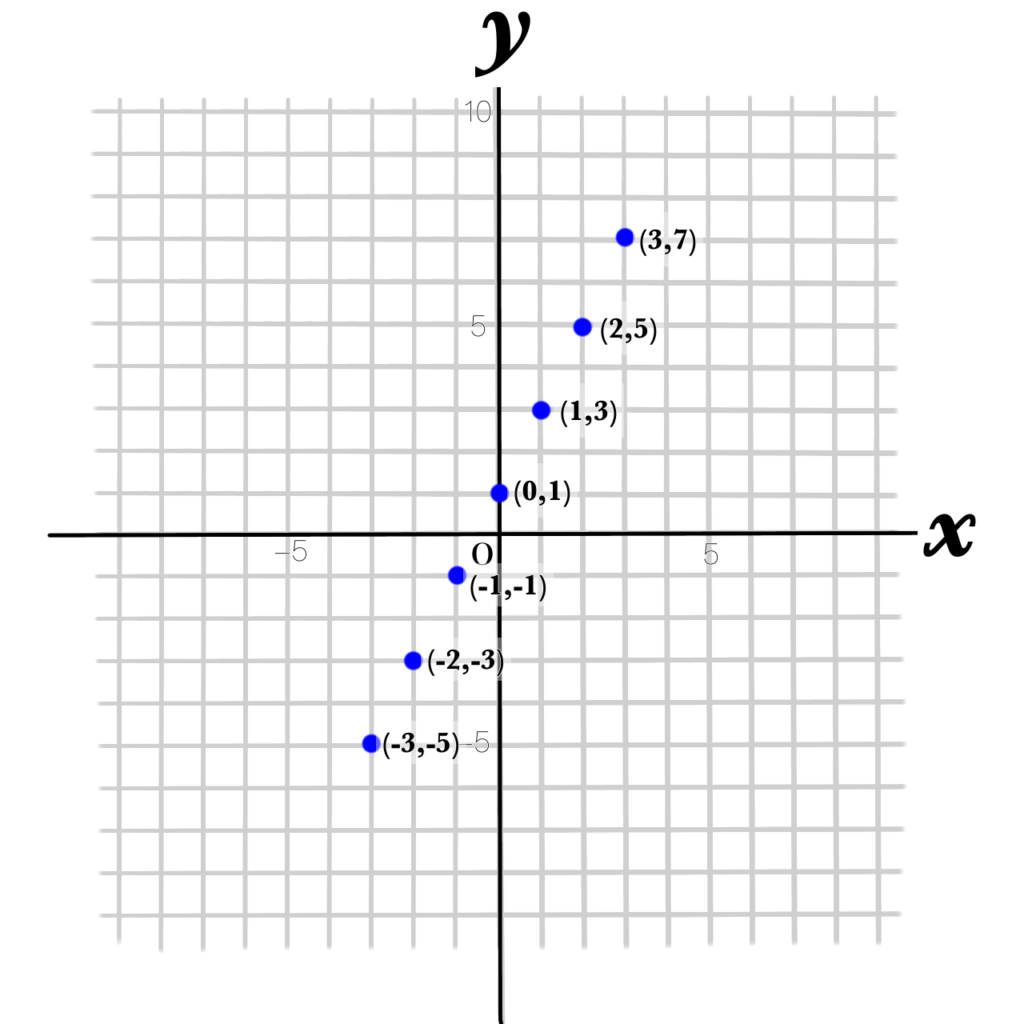
この点を結び、その線を延長していきます。
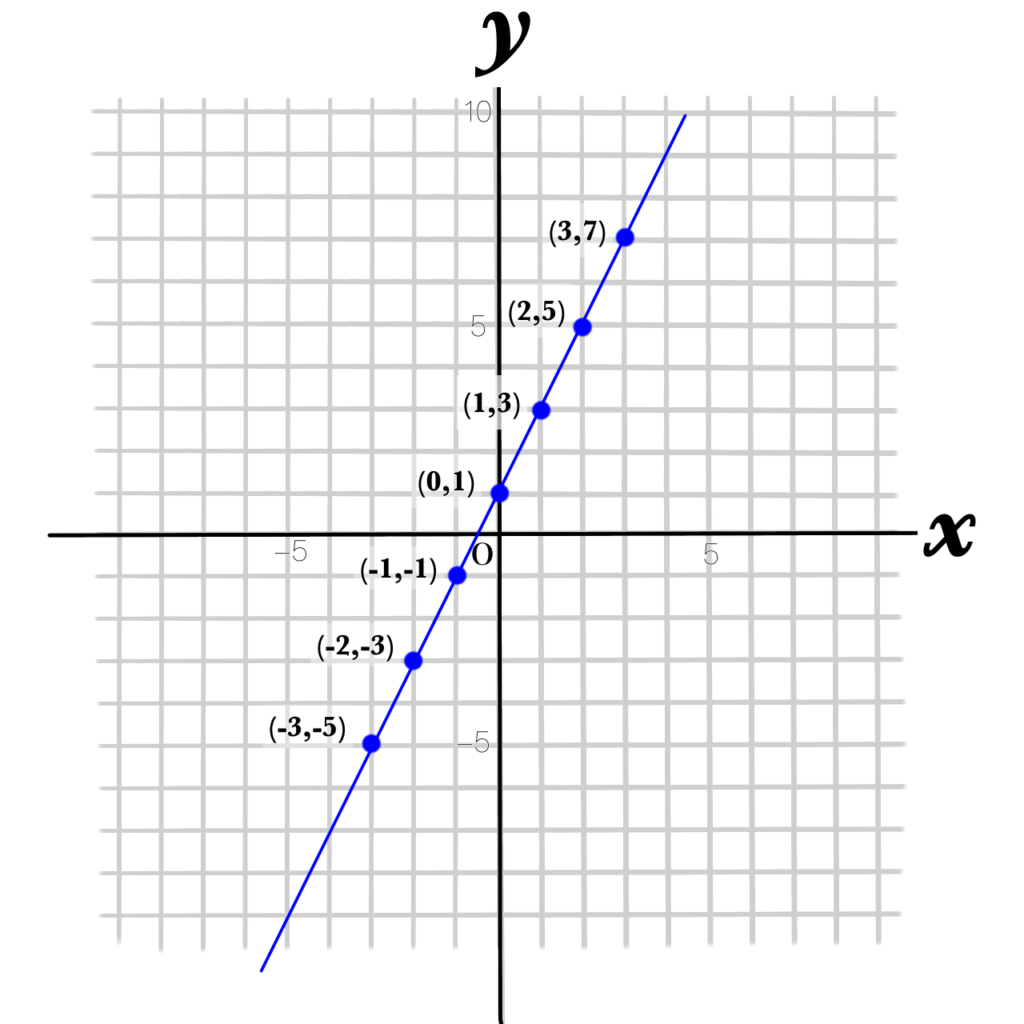
そうすると直線になります。一次関数は必ず直線のグラフになるのです!

グラフの傾向を見ていこう!&用語解説
切片とは?
式と表
式
\(y=2x\)\(+1\)
表
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| \(y\) | -5 | -3 | -1 | 1 | 3 | 5 | 7 |
グラフ
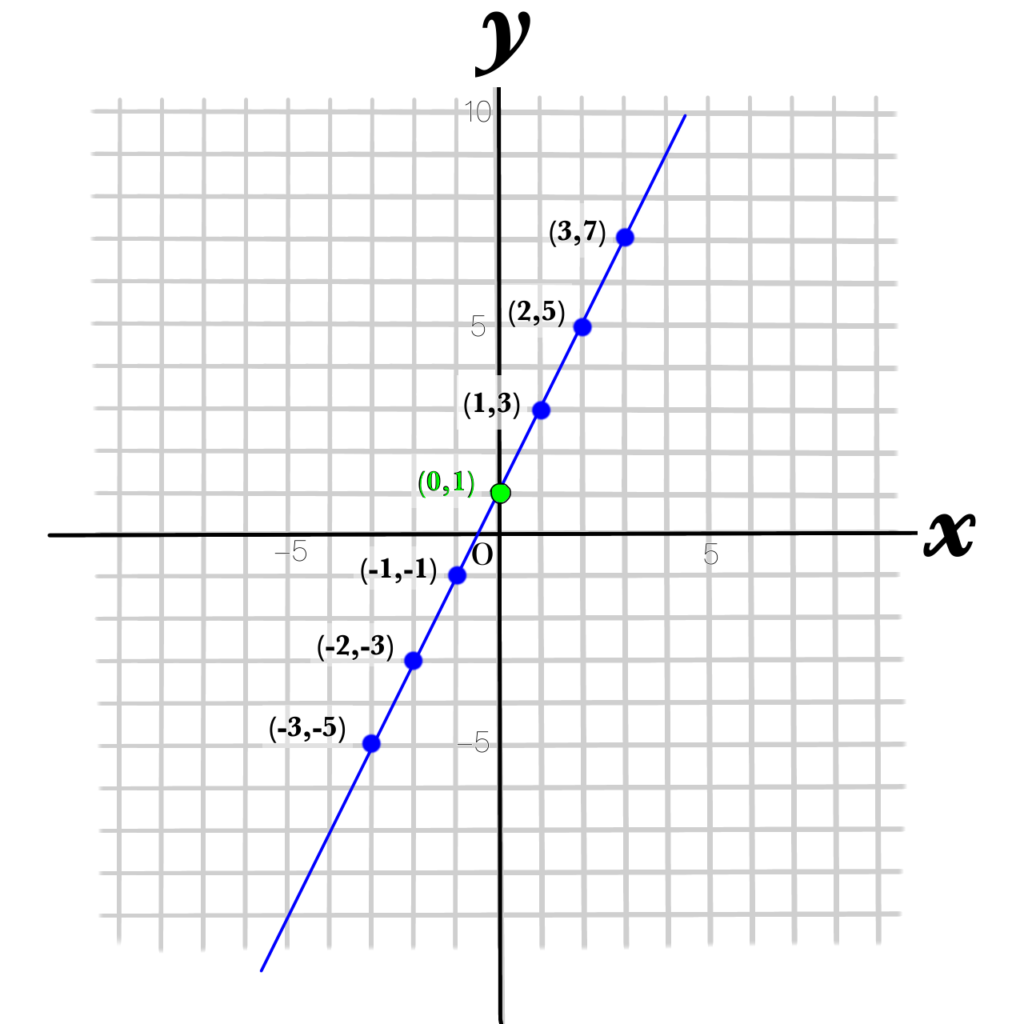
\(x\) が0のとき、0は何をかけても0になるので、\(y\) の値は、緑で示した数字の部分(上の例では1)になります。
この、\(y\) 軸上の点を「切片」と言います。
直線が\(y\) 軸をシャキーン!と切っている点という感じ?ってことでしょうか。
…「シャキーン」って効果音はいらないですね(笑)
一次関数の一般的な形
\(y=ax+b\)
で言えば、\(+b\) の部分が「切片」と言う、ってことですね。
傾きとは?
式と表
式
\(y=\)\(2\)\(x+1\)
表
グラフ
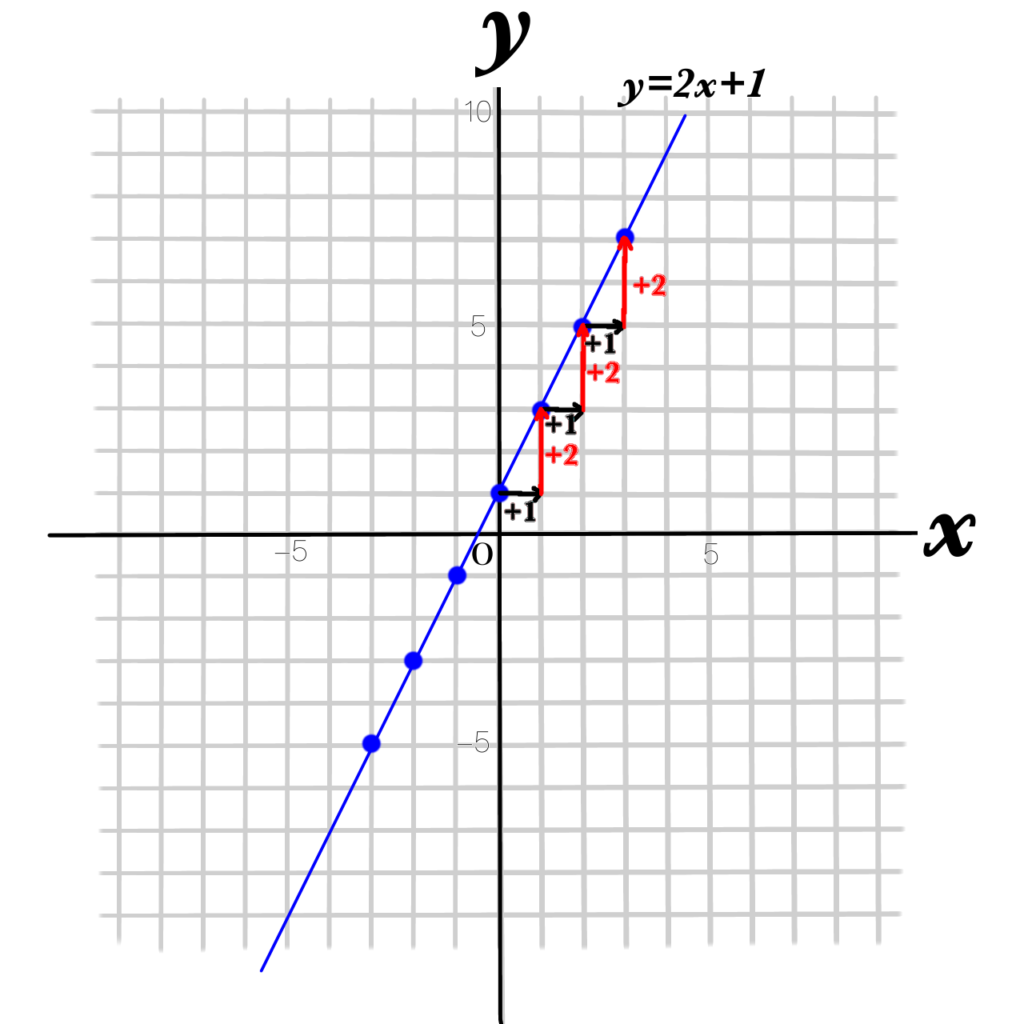
\(x\) が1つ増えるごとに、\(y\) は2つ増えています。そしてそれが式の中の赤文字で示した部分と同じになります。
このように、\(x\) が1増えたときに、\(y\)がいくつ増えるか、減るかが表れる数が、\(y=ax+b\)中の \(a\) になり、この部分を「傾き」と言います。
\(y=4x+1\)
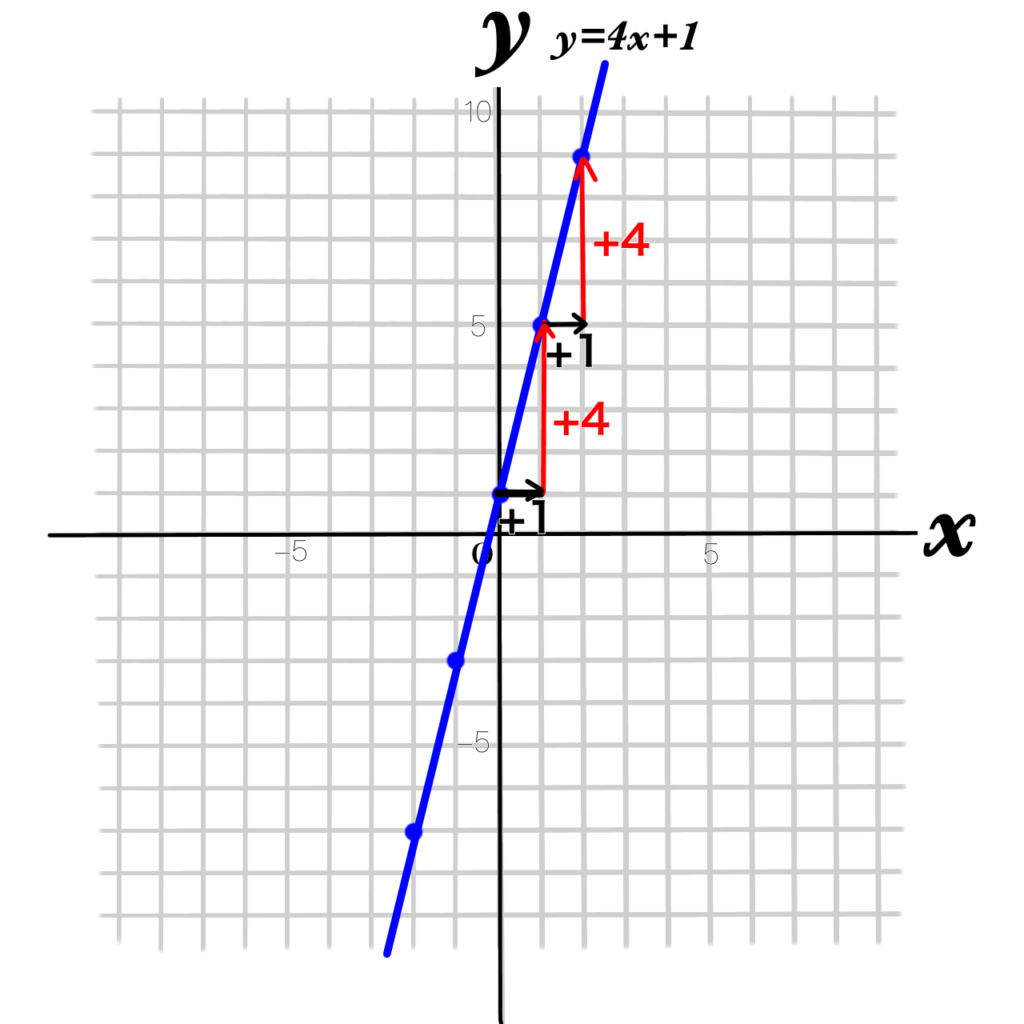
\(x\) が1つ増えると
\(y\) が4つ増えている。
だから傾き4
\(y=\dfrac{1}{2}x+1\)
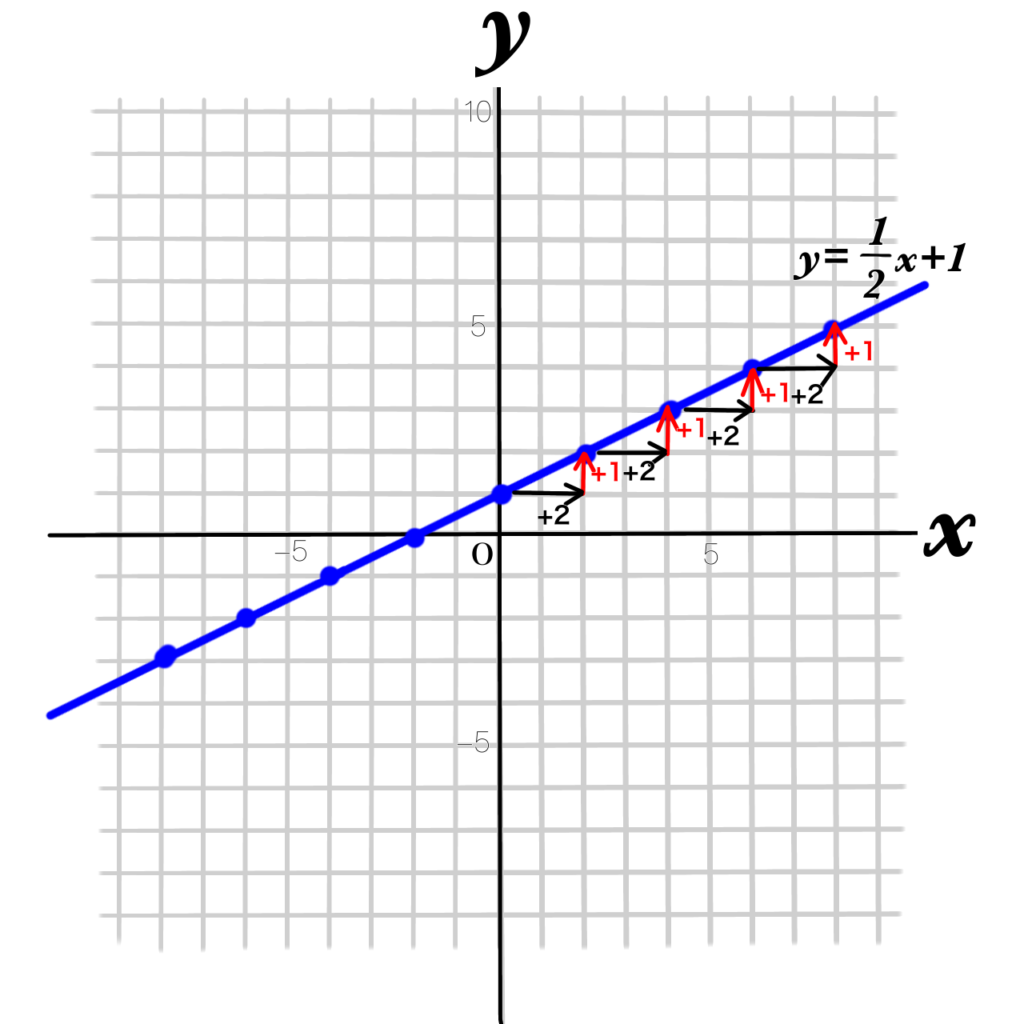
\(x\) が2つ増えると
\(y\) が1つ増えているから、
\(x\) が1つ増えると
\(y\) は\(\dfrac{1}{2}\)増えることになる。
だから傾き\(\dfrac{1}{2}\)
\(y=-x+1\)
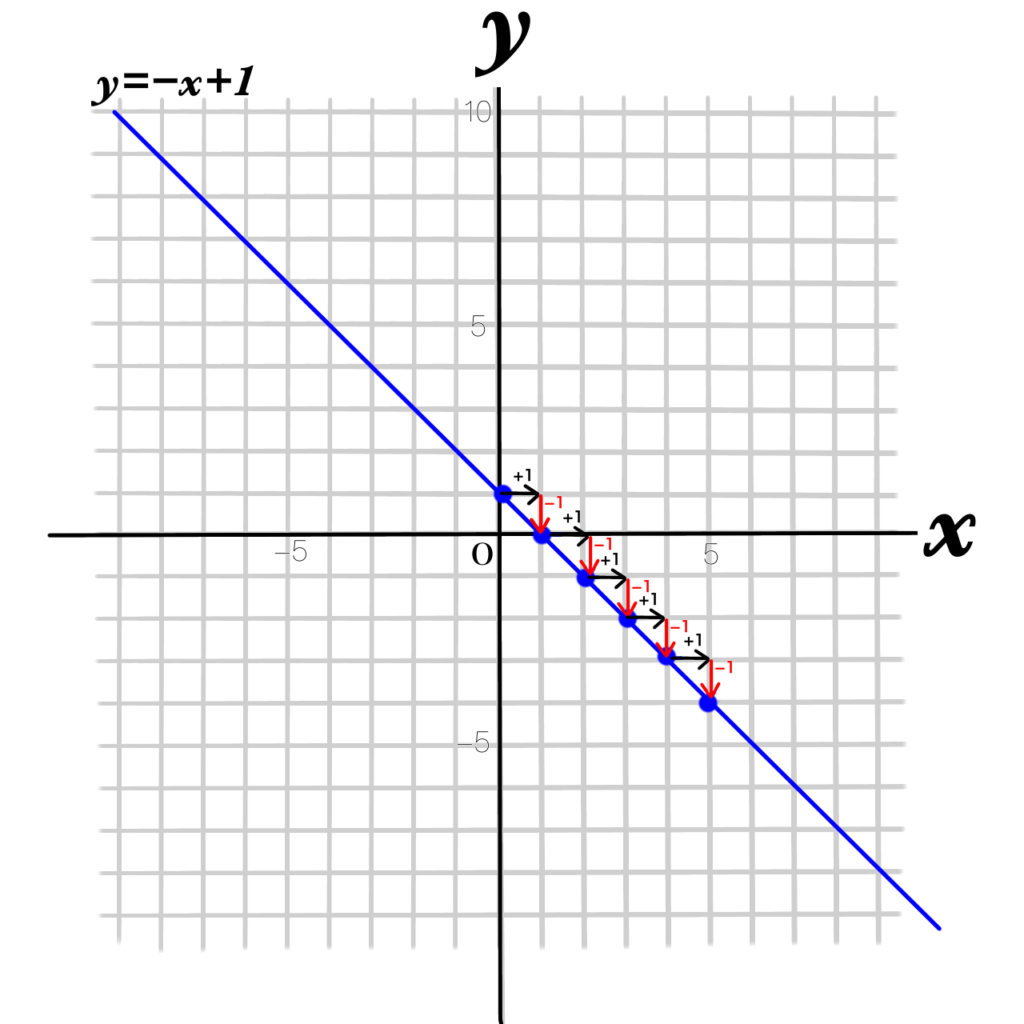
\(x\) が1つ増えると
\(y\) が1つ減っている。
減った場合はマイナスで表すので、傾き-1

数字が大きくなると速いすべり台
数字が小さくなるとノロノロすべり台
になるの?

すべり台とはおもしろい。
まぁそういうことじゃな。
数字が「-」になったらどうなる?

逆のすべり台!

感覚的には間違っておらぬ。
すべり台は別として、次のことが言えます。
| +やーの符号は置いといて、 傾き(\(a\)の値)の数字が大きくなると | 急なグラフになる |
| +やーの符号は置いといて、 傾き(\(a\)の値)の数字が小さくなると | ゆるやかなグラフなる |
| 傾き(\(a\)の値)の数字がプラスだと | 右上がりのグラフになる |
| 傾き(\(a\)の値)の数字がマイナスになると | 右下がりのグラフになる |
\(y=ax+b\)の\(a\)に入る数字によってグラフの傾き方が違ってきます。だから\(a\)の値を「傾き」と言うわけです。
こういう傾向になることをグラフに書きながら感覚的に覚えていきましょう。すべり台をイメージしてもいいですよ(笑)
変化の割合とは?
\(変化の割合=\dfrac{yの増加量}{xの増加量}\)
このような公式を見たことがあると思います。さて、これは何を意味しているのでしょうか?

↑…何を言っているのか分かりません。スルーしましょう(笑)
各用語の説明をします。

\(xの増加量\)=\(x\)がいくつ増えたか?
\(yの増加量\)=\(y\)がいくつ増えたか?
これが「増加量」の意味です。
「増加量」とか、漢字ばかりだといかにも難しいイメージになりがちですが、別に難しいことはありません。
例えば、4個で800円のものがあったら、1個何円か?みたいな計算をする場面がありますよね?
変化の割合の計算はまさにそれです。「1つ当たりいくらか」を考えているのです。
これを\(x\) と\(y\)に置き換えると、\(x\) が1つ増えたときに、\(y\) がいくつ増えるのか、減るのかを出している計算。それが「変化の割合」です。
ところで、「\(x\) が1つ増えたときに、\(y\) がいくつ増えるのか」ってどこかで聞いたことがありませんか?

さっき出てきた!
傾きと同じだ‼
そうなんです!一次関数では、「傾き」と「変化の割合」は同じなんです!
傾きが分かれば変化の割合が分かるし、変化の割合が分かれば傾きも分かるんです!
変化の割合の問題
問題1 一次関数\(y=3x-5\)について、\(x\)の値が次のように変化した時の変化の割合を求めなさい。
(1)2から5まで
(2)-3からー1まで
さて、答えは何でしょう?
正解はどちらも3です。
一次関数では必ず
変化の割合=傾き(\(a\)の値)
これが成り立ちます!ですので、どこの区間だろうが変化の割合は傾きと同じになるのです。
この問題は式が\(y=3x-5\)ですので、傾きは3です。ならば、変化の割合も3です。特に計算する必要はありません!

でも、計算の方法も学習したと思います。その計算方法で解くために、もう一度さっきの問題を登場させて解いてみましょう。
問題1 一次関数\(y=3x-5\)について、\(x\)の値が次のように変化した時の変化の割合を求めなさい。
この計算のポイント
①\(x\)の値を式に入れて、\(y\)の値を出すこと
②\(x\)と\(y\)を対応する順番で書いて引き算すること
(1)2から5まで
| 式 | \(x\)の値 | 計算 | \(y\)の値 |
| \(y=3x-5\) | 2 | \(y=3\times 2-5=6-5=1\) | 1 |
| \(y=3x-5\) | 5 | \(y=3\times 5-5=15-5=10\) | 10 |
| ↓ | ↓ | ||
| \(x\)の増加量 の計算 | 5-2 | \(y\)の増加量 の計算 | 10-1 |
\(変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{10-1}{5-2}\)
\(=\dfrac{9}{3}=3\)
(2)-3からー1まで
| 式 | \(x\)の値 | 計算 | \(y\)の値 |
| \(y=3x-5\) | -3 | \(y=3\times \left( -3\right)-5=-9-5=-14\) | -14 |
| \(y=3x-5\) | -1 | \(y=3\times \left( -1\right)-5=-3-5=-8\) | -8 |
| ↓ | ↓ | ||
| \(x\)の増加量 の計算 | (-1)-(-3) | \(y\)の増加量 の計算 | (-8)-(-14) |
\(変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{\left( -8\right) -\left( -14\right) }{\left( -1\right) -\left( -3\right) }\)
\(=\dfrac{6}{2}=3\)
やはりどちらの答えも傾きと同じ3になりました。
傾きがそのまま答えなのに、なぜ計算方法を教えるのでしょう?


違うでおじゃる(即答)

一次関数のときは変化の割合と傾きが同じですが、そうなるのは一次関数だけです。
グラフが直線になるものだけの特別な特徴なんです。
反比例の式は
\(y=\dfrac{a}{x}\)
となっていて、確かに\(a\)という文字はありますが、これは「傾き」ではありません。グラフが直線にならなければ、変化の割合=\(a\)ではないので、間違えないように注意しましょう!
反比例などの曲線になるグラフで変化の割合を求める問題があった場合は、この計算を使わないと解けないので覚えておいた方が良いです。
変化の割合を利用した問題
第2問 一次関数\(y=-2x+3\)で、\(x\)の増加量が3のときの\(y\)の増加量を求めなさい。
この問題をもっと簡単な言葉で言うと
\(y=-2x+3\)の式で、\(x\)が3つ増えたとき、\(y\)はいくつ増えますか?
という問題です。
一次関数の傾き(変化の割合)は「\(x\)が1つ増えたとき、\(y\)がいくつ増えるか、減るか」が表れる数でした。
この問題では傾き(変化の割合)は\(-2\)なので、\(x\)が1つ増えたとき、\(y\)が2つ減ることを意味しています。
そうすると、\(x\)が3つ増えたときは\(y\)はどうなるでしょう?
| \(x\) | \(y\) | |
| 増える量 | 1 | -2 |
| 2 | -4 | |
| 3 | -6 |
表のように\(x\)が3増えると、\(y\)は6減ります。\(x\)の増える量が3倍になれば、\(y\)の増える量も3倍になる、ということですね。
ですので、答えは―6となります。
計算としては、-2×3=-6
この問題でよくある間違い!
\(x\)の増加量を、式の\(x\)のところに入れて、\(y\)を求める計算をしてしまう
✖\(y=-2x+3\)に\(x\)の増加量3を代入して、\(y=-2\times3+3=-6+3=-3\)✖
↑これは、「\(x=3\)のときの\(y\)の値を求めなさい」と言う問題の解き方です!
ここでは\(y\)の値ではなく、\(y\)の増加量を求めているので勘違いしないように注意しましょう。
基本編まとめ
| 一次関数の式 | \(y=ax+b\) | a=傾き | b=切片 |
| グラフ | 直線になる | \(x\)が1つ増えたときに\(y\)がいくつ増えるか、減るかを示している | グラフが\(y\)軸上のどこの点を通るかを示している |
| その他 | 変化の割合に等しい。 |
一次関数の基本編は以上です!次の記事では「一次関数の実践編」として、グラフの書き方、読み取り方、グラフの式の求め方を説明したいと思います。



コメント