平方根の意味
平方根とは?
2乗すると、〇〇になる数。これが〇〇の平方根の意味です。…という説明では意味不明ですね。以下をご覧ください。
| 問題 | 意味 | 答え | 答え方 |
| 9の平方根 | 2乗すると9になる数 | 3とー3 | ±3 |
| 16の平方根 | 2乗すると16になる数 | 4とー4 | ±4 |
表の「答え方」のように「±」って感じで省略して書くのが普通です。
このように、普通の数字で出る分にはいいんですが、出ない場合もあります。
5の平方根(2乗すると5になる数)は?という問題が出てきた時などがそうです。
2乗して5になる数って、普通には考えられないですよね。
その時に登場するのがルートです。
「2乗すると5になる数を√ 5と表しましょう。」
というきまりで作られた数がルートの数なんですね。
ですから、5の平方根は ± √ 5となります。
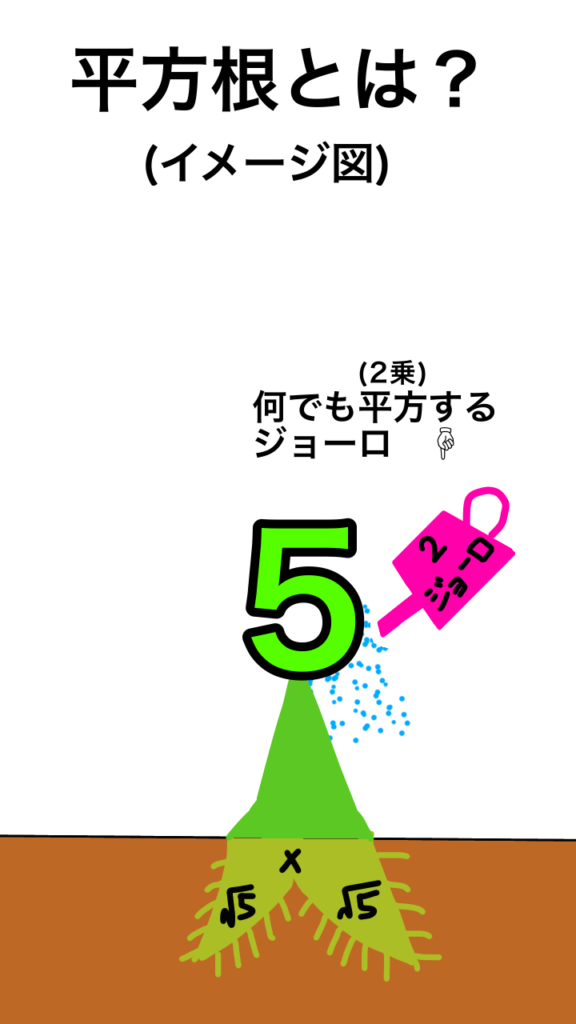
√ の数の性質
逆に言えば、√5という数は、2乗すると5になるという決まりのもとにできている数と言うこともできます。
√5 ² = 5
このように、ルートの数は、2乗されるとすかさず2乗とルート(√)ははずれます。
√25を考えてみましょう。
| √25 | 25は5²です。 |
| √25=√5² | 2乗になると√ がはずれますので、 |
| √25=√5²=5 | と、このように計算していきます。 |
2乗の数が出てきた時に目ざとく見つけて変形することが重要!ということですね。
それでは、√12 のような場合はどうでしょう?12という数は、何かの2乗の数ではありません。
でも、12を分解すると
12=2×2×3=2²×3
と、このように2乗の数が現れます。こういう場合も変形していかなければなりません。
| √12 | 12を分解していきます。 |
| √2²×3 | 2が2乗になったので、 2だけ√ がはずれます。 |
| 2√3 | これで変形終了です。 |
これが鉄則です。中2までは出て来なかった数なので、なかなかイメージしづらいと思いますが、「ルートは2乗になったらはずれる」。それを頭に入れて計算していきましょう。
イメージ動画を作ったので、参考にご覧ください。
イメージ動画↓
平方根のかけ算
計算のしかた
√ 5 × √2 = √ 10
このようにルートの数はルートの数どうしでかけ算することができます。
4 √ 2 × 5 √ 5= 20 √ 10
整数は整数同士かけ算できますので、この例の場合、整数を整数同士、ルートはルート同士の掛け算になります。
整数の数とルートの中の数は、世界が違う数なので、直接計算することはできません。
そしてこの場合も注意して欲しいのは、2乗になればルートがはずれるということです。
例1:√2 × √18の計算
| √2 × √18 | √ の中は√ の中同士で計算できるので √2×18 を計算 |
| = √36 | このようになりますが、2乗の数に注意! |
| = √6² | 2乗になると√ がはずれます。 |
| = 6 | これで計算終了です。 |
例2 2√3× 3√6の計算
| 2√3× 3√6 | 整数は整数どうし、 √ の数は√ の数どうしを計算します。 |
| = 6√18 | √ の中を分解して、 2乗になる数があるかどうかを確認します。 |
| =6√3²×2 | 2乗の数は√ がはずれます |
| =6×3√2 | 整数は整数どうしでかけ算できます。 |
| =18√2 | これで終了です。 |
2乗になる数に注意して計算しましょう。
かけ算でよくある間違い
よくある間違い①

√2×√18=√36と答えを出したらはずれました。なぜですか?

36は何かの2乗の数ではないですか?

6の2乗です。

2乗になったら√ をはずしましょう。

√36=√6²=6
でいいですか?

それで正解です。
よくある間違い②

計算したら√35になりました。
分解したら√5×7だったので5√7と答えたらハズレ。なぜ?

2乗にならないとルートははずれません。

√35は数が大きいから小さくしなきゃじゃないの?

「大きい数だから」じゃなく、2乗の数だから√ をはずすんですよ。

じゃあ、√35で答え?

それで正解です。
よくある間違い③

2√6×3√10=6√60
√60=√2²×3×5なので答えは2√15としたらハズレました。どうしてでしょう?

√60を2√15としたのは正解ですが、6√60の計算でしたよね?

あ!そうか!…でも、
6と2√15は+ですか?×ですか?

6√60は6×√60の×を省略したものです。

なるほど!かけ算ですね!
6√60=6×2√15=12√15
これで合ってますか?

それで正解です。
よくある間違い3つを紹介しました。慣れないとしてしまいがちなので、注意して解きましょう。
また、答えが+なのか−なのかは、平方根に限らずいつも注意して計算するようにしてください。
平方根の割り算
計算のしかた・有理化
√ 6 ÷ √ 3 = √ 2
このようにルートはルート同士割り算ができます。でも、
√5 ÷ √3
5 ÷ 3はできませんよね。この場合分数で表します。これは整数と変わりません。
√5 ÷ √3 = ![]()
しかし、平方根の場合、分母にルートが付くと分母の有理化を行わければなりません
分母の有理化とは、分母にルートの数があるときにそれを整数に直すことです。
分母の有理化(基本手順)
 | 分母の√3を通分と同じ要領で分母と分子にかけます。 |
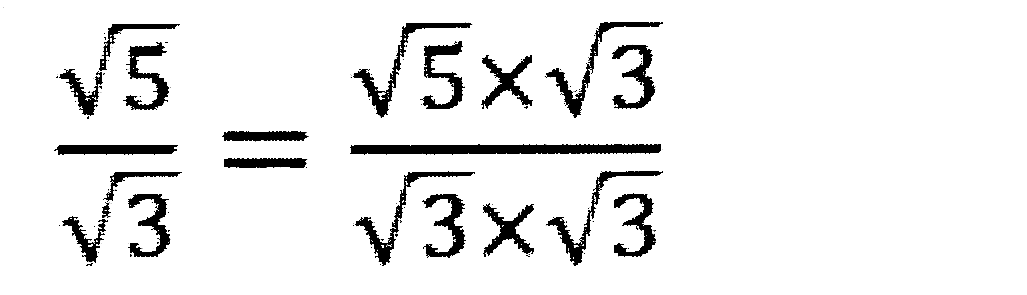 | 分母が√3²になるので、ルートがはずれて3になります。 |
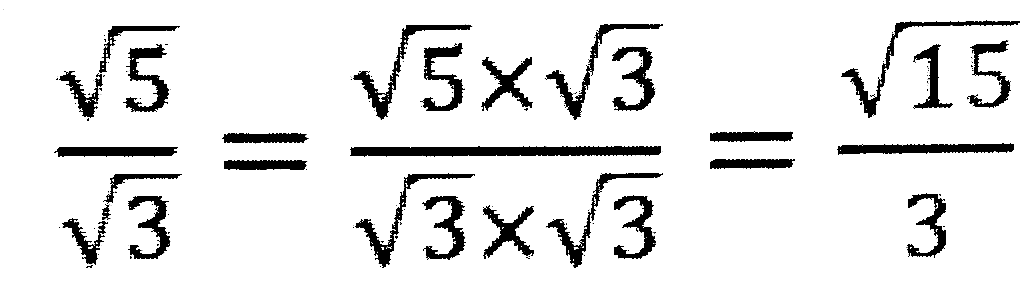 | これで有理化の終了です。 |
この処理を必ずしてください。
なぜ有理化は必要か
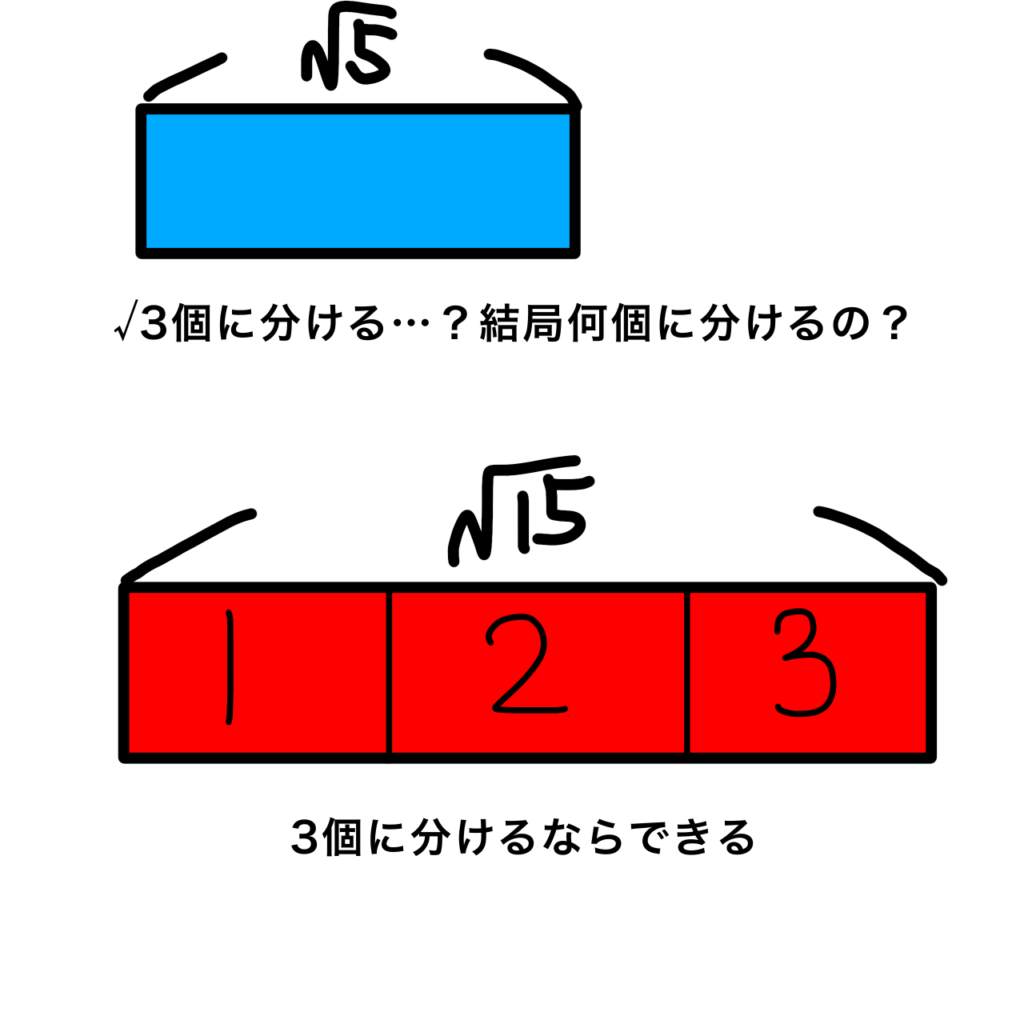
「√5のものを√3 個に分ける」
ルート3個に分ける?結局いくつに分けるの?となりますよね。
でも、
「√15を3個に分ける」
と聞けば√15自体が何かよく分からなくても、そこにあれば3等分する事はできそうですよね。
つまり有理化をすることによって数が少し考えやすくなるんです。それが有理化の効果じゃないでしょうか。
平方根の足し算・引き算
計算のしかた・考え方
平方根の足し算・引き算は、同じ種類(√ の中が同じ数字)のものが何個あるかという計算です。
√5であれば、√5が何個あるか?
√3であれば、√3が何個あるか?
そういう計算になることを覚えておきましょう。つまり同類項の計算と同じなのです。
2x+3x=5x
これは、xが2個とxが3個を合わせてxが5個あるから、5xになっていると言うことですよね。これはルートの計算も同じです。
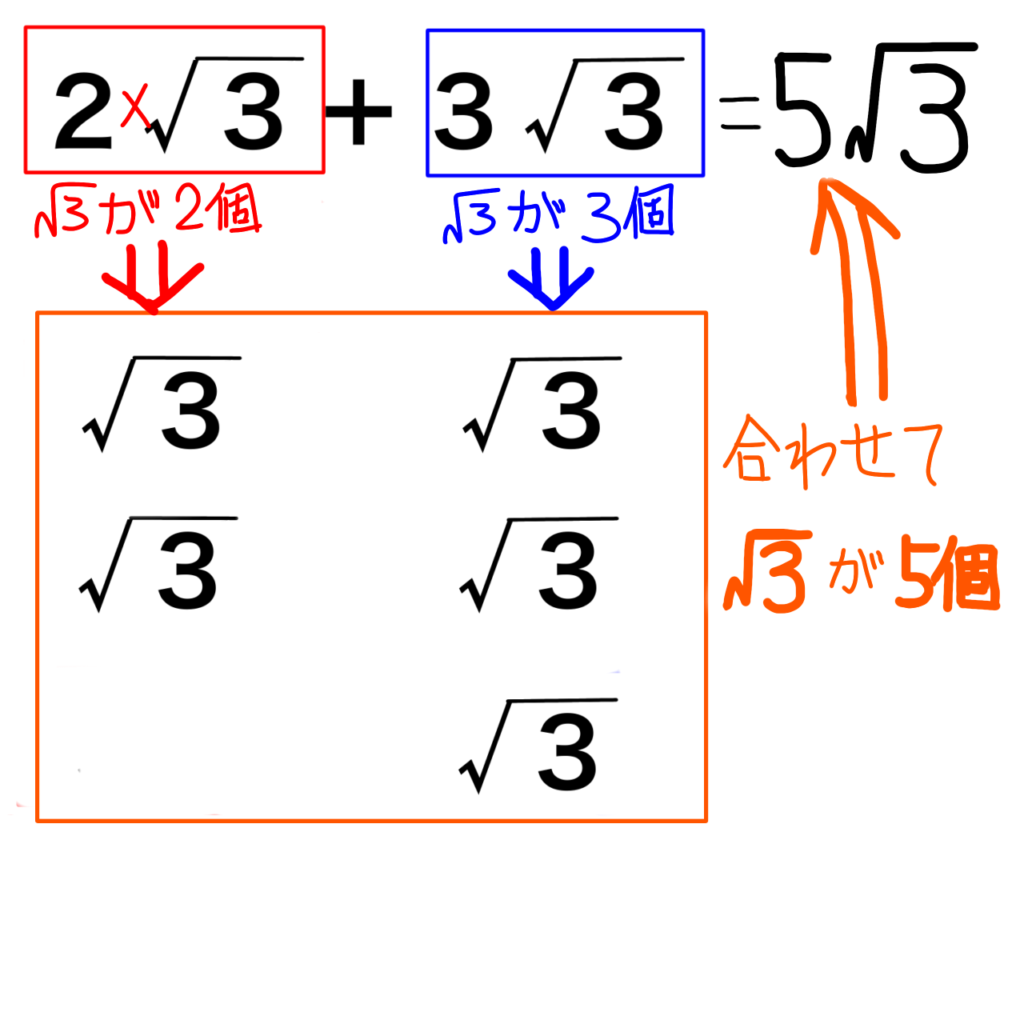
2√3+3√3=5√3
これも√3が2個と√3が3個を合わせて√3 が5個あるから5√3になるということです。この考えは引き算でも同じです。
3√5+2√2ー4√2+5√5
このような問題の場合も、√5は√5どうし、√2は√2どうしの計算をすれば終了です。
3√5+2√2ー4√2+5√5=8√5ー2√2
答え 8√5ー2√2
これ以上足せませんので注意しましょう。
ルートのたし算、引き算でよくある間違い
よくある間違い①

6√2 −2√2+√2 = 4√2 と答えたら間違いって言われたんですけど!なんで?

√ の前に数字がない場合は1が省略されていますよ。

6√2 −2√2+1√2 ってこと?
じゃあ答えは5√2 ?

それで正解です!
よくある間違い②

√8+√2=√10 としたらハズレちゃいました。なぜぇ?

ルートの中どうしは、足したり引いたりできませんよ。

え?じゃあどうすればいいの?

√8=√2²×2なので、ルートの中を簡単にできますよ。

あ!√8=2√2?
2√2+√2=えっと…

√ の前に数字がないのは1が省略されてますよ。

2√2+1√2ってこと?あそっか!
じゃあ答えは3√2 ?

正解です!
よくある間違い③

3√2+4√2
=7√4
=7√2²
=7×2
=14
どうですか?

√ の中は足せませんよ。
√2が3個と√2が4個。√2は合わせていくつありますか?

√2が7個です。

その考え方と同じです。

3√2+4√2=7√2ということですね!

正解です!
混乱してしまいがちなので注意して計算しましょう。
平方根の計算で注意すべきところはこのようなところです。他にもポイントはありますが、実際に練習をしてみて、トライ&エラーでやってみましょう!
平方根の計算 ポイントまとめ
ポイントのまとめ
| ①ルートの数は、2乗になればルートが外れる! |
| ②ルートの中はできるだけ簡単な数にする! |
| ③整数は整数どうしルートはルートどうしで掛け算・割り算ができる! |
| ④分母に√ がある場合は、必ず有理化を行う! |
| ⑤ルートの足し算・引き算は、同類項の計算と同じ! |
平方根(乗法・除法)の問題(解答解説付き)
問題 ポイント 解答・解説動画
問題・ポイント
解答・解説
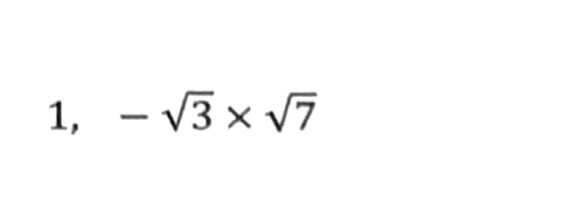
1問目ポイント
③整数は整数どうしルートはルートどうしで掛け算・割り算ができる!
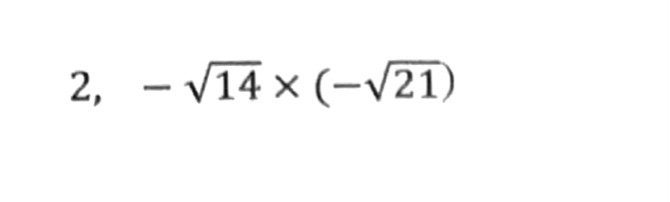
①ルートの数は、2乗になればルートが外れる!
②ルートの中はできるだけ簡単な数にする!
③整数は整数どうしルートはルートどうしで掛け算・割り算ができる!
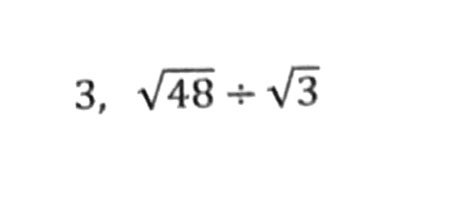
①ルートの数は、2乗になればルートが外れる!
③整数は整数どうしルートはルートどうしで掛け算・割り算ができる!
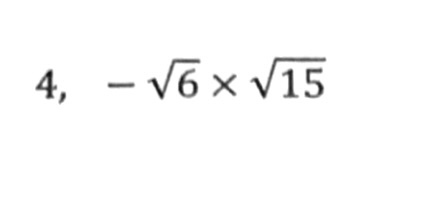
①ルートの数は、2乗になればルートが外れる!
②ルートの中はできるだけ簡単な数にする!
③整数は整数どうしルートはルートどうしで掛け算・割り算ができる!
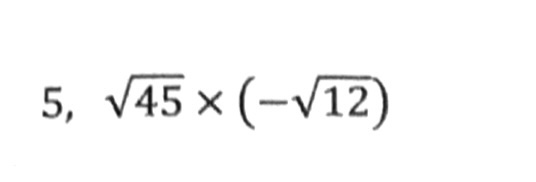
①ルートの数は、2乗になればルートが外れる!
②ルートの中はできるだけ簡単な数にする!
③整数は整数どうしルートはルートどうしで掛け算・割り算ができる!
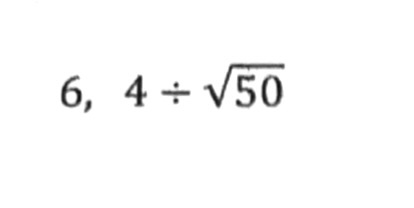
①ルートの数は、2乗になればルートが外れる!
②ルートの中はできるだけ簡単な数にする!
④分母に√ がある場合は、必ず有理化を行
解答だけ見たい人はこちらをどうぞ!

平方根(加法・減法)の問題(解答解説付き)
問題 ポイント 解答・解説動画
問題・ポイント
解答・解説動画
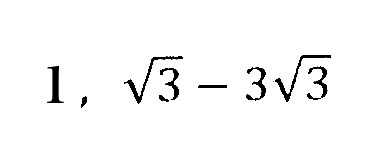
⑤ルートの足し算・引き算は、同類項の計算と同じ!
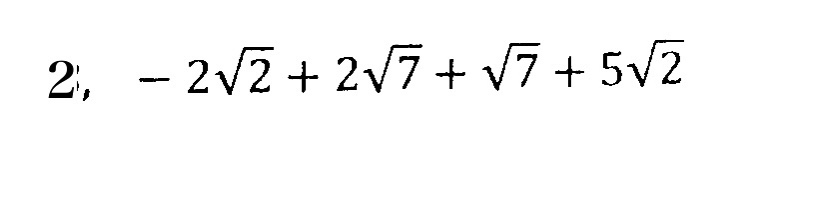
⑤ルートの足し算・引き算は、同類項の計算と同じ!
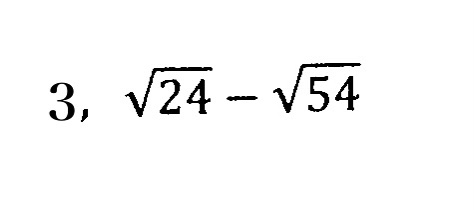
②ルートの中はできるだけ簡単な数にする!
⑤ルートの足し算・引き算は、同類項の計算と同じ!
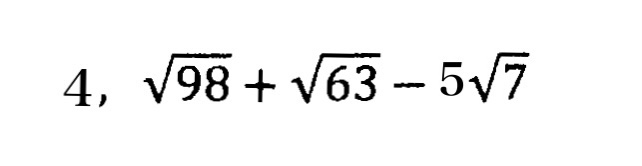
②ルートの中はできるだけ簡単な数にする!
⑤ルートの足し算・引き算は、同類項の計算と同じ!
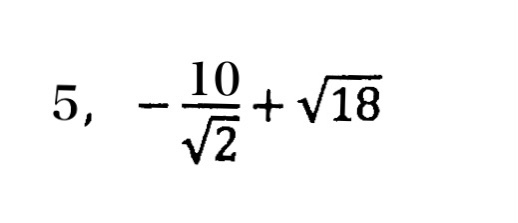
②ルートの中はできるだけ簡単な数にする!
④分母に√ がある場合は、必ず有理化を行う!
⑤ルートの足し算・引き算は、同類項の計算と同じ!
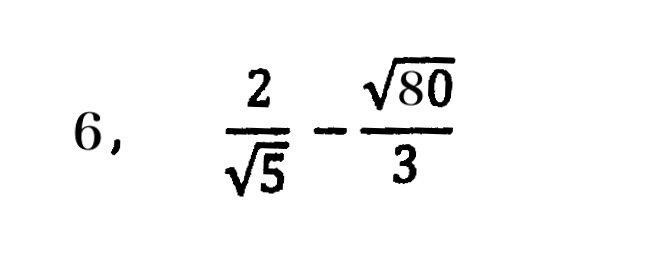
②ルートの中はできるだけ簡単な数にする!
④分母に√ がある場合は、必ず有理化を行う!
⑤ルートの足し算・引き算は、同類項の計算と同じ!
解答だけ見たい人はこちらをどうぞ!
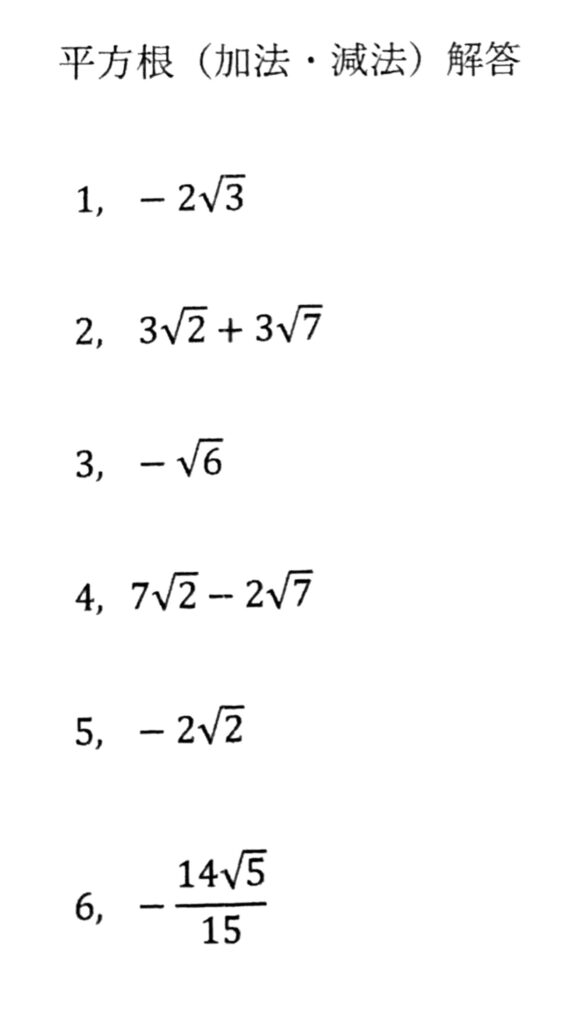
だいたい解き方が分かったら、教科書や問題集の問題も解いてみましょう!


コメント