学校ではこの2つの解き方を学習します。
①傾きか切片かどちらか分かる場合の解き方
②連立方程式を使う解き方
まずはこの2つについて説明します。
最後に私がよく使っている求め方も紹介しますので、チャンネルはそのままで!

テレビ番組でCMにいくときのやつ!
①傾きか切片かどちらか分かる場合の解き方
| ①問題文に「直線」とか「一次関数」が出てきたときには、 「\(y=ax+b\)」を思い浮かべる |
| ②傾きが分かっていれば\(a\)にその数字代入。 切片が分かっていれば\(b\)にその数字を代入します |
| ③座標が1つ分かっているので、\(x\)座標の数を\(x\)に、 \(y\)座標の数を\(y\)に代入してできた方程式を解きます。 |
| ④\(y=ax+b\)の\(a\)と\(b\)のところに それぞれの数を代入して完成です! |
実際にやってみましょう!
例題1 傾きが3で、点(-1,4)を通る直線の式を求めなさい。
| ①「直線」なので\(y=ax+b\) | \(y=ax+b\) |
| ②傾きが3なので、 傾き\(a\)に3を代入します。 | \(y=3x+b\) |
| ③(-1,4)なので、 \(x\)に-1、\(y\)に4 を代入して計算します。 | \(4=3\times \left( -1\right) +b\) \(4=-3+b\) \(-3+b=4\) \(b=4+3\) \(b=7\) |
| 傾き\(a=3\)、切片\(b=7\) となったので \(y=ax+b\)に代入して完成です。 | \(y=3x+7\) |
例題2 切片が-2で、点(-3,10)を通る直線の式を求めなさい。
| ①「直線」なので\(y=ax+b\) | \(y=ax+b\) |
| ②切片が-2なので、 切片\(b\)に-2を代入します。 | \(y=ax-2\) |
| ③(-3,10)を通る直線なので \(x\)に-3、\(y\)に10 を代入して計算します。 | \(10=a\times \left( -3\right) -2\) \(10=-3a-2\) \(-3a-2=10\) \(-3a=10+2\) \(-3a=12\) \(a=-4\) |
| 傾き\(a=-4\)、切片\(b=-2\) となったので \(y=ax+b\)に代入して完成です! | \(y=-4x-2\) |
例題3 \(y=2x+3\)に平行で、点(-4,-2)を通る直線の式を求めなさい
「平行」ということは、「傾きが同じ」ということです。もちろん切片は違います。
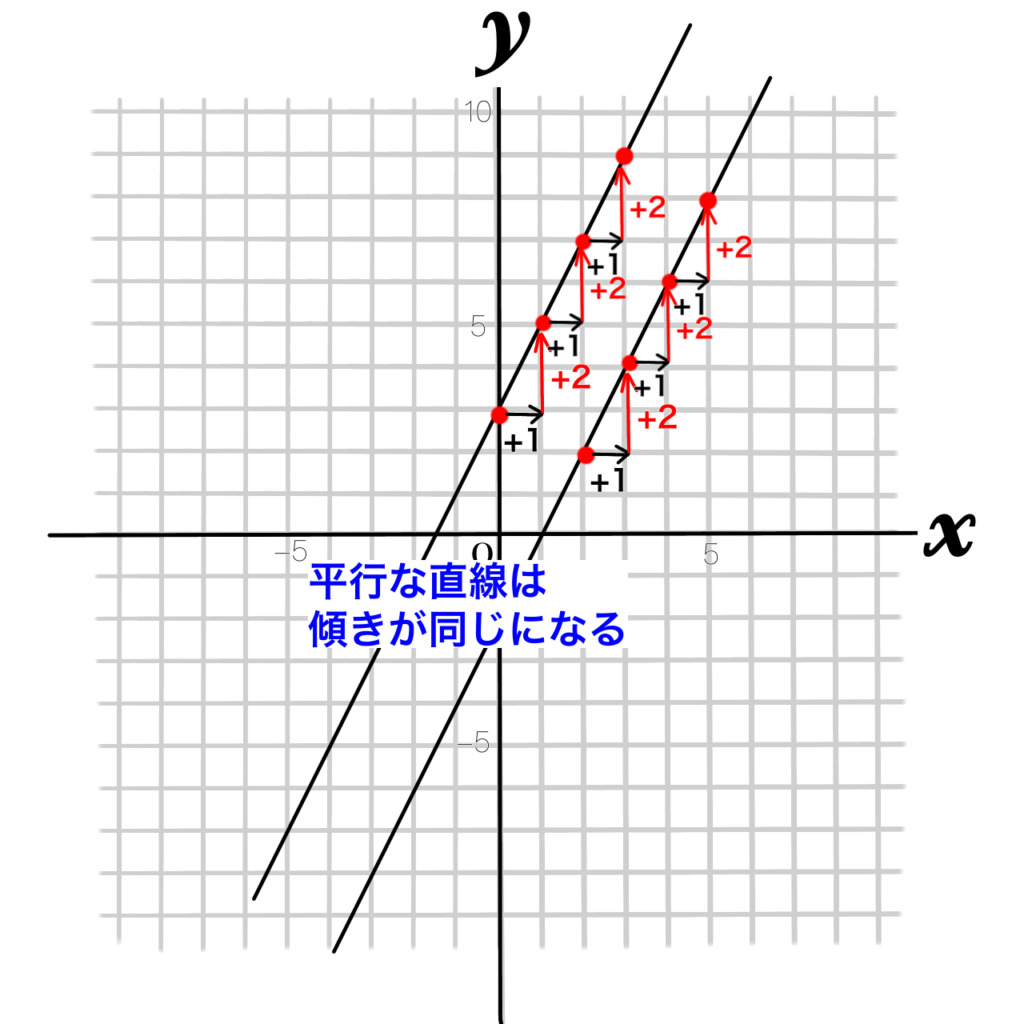
\(y=2x+3\)に平行な直線を求めるので、傾きが2になることを示しています。
この問題を言い換えると、「傾きが2で、点(-4,-2)を通る直線の式を求めなさい」という問題と同じです。
| ①「直線」なので\(y=ax+b\) | \(y=ax+b\) |
| ②傾きが2なので、 傾き\(a\)に2を代入します。 | \(y=2x+b\) |
| ③(-4,-2)を通るので、 \(x\)に-4、\(y\)にー2 を代入して計算します。 | \(-2=2\times \left( -4\right) +b\) \(-2=-8+b\) \(-8+b=-2\) \(b=-2+8\) \(b=6\) |
| 傾き\(a=2\)、切片\(b=6\) となったので \(y=ax+b\)に代入して完成です。 | \(y=2x+6\) |
例題4 2点(2,-1)(5,-4)を通る直線の式を求めなさい。
| ①「直線」なので\(y=ax+b\) | \(y=ax+b\) |
| ②2つの点を\(x\)座標同士、 \(y\)座標同士で比べると、 \(x\)は2⇒5 3つ増えています。 \(y\)は(-1)⇒(-4) 3つ減っています。 傾き=\(\dfrac{yの増加量}{xの増加量}\) =\(\dfrac{-3}{3}=-1\) よって傾き\(a\)は-1です。 \(a\)に-1を代入します。 | \(y=-1x+b\) |
| ③2点(2,-1)(5,-4) どちらかを式に代入しましょう。 お好みでOKです。 ここでは(2,-1)にしますね。 \(x\)に2、\(y\)に-1 を代入して計算します。 | \(-1=-1\times 2 +b\) \(-1=-2+b\) \(-2+b=-1\) \(b=-1+2\) \(b=1\) |
| 傾き\(a=-1\)、切片\(b=1\) となったので \(y=ax+b\)に代入して完成です! | \(y=-x+1\) |
このように、「傾きか切片のどちらか」+「1つの点の座標」が分かれば計算で解けます。


「直線の傾き」から、
世の中から傾いているもの→傾き者(かぶきもの)→歌舞伎となった、
っていう歴史を使ったボケですよね?分かりづらすぎます!
しかもクオリティ低すぎ!「っぽいもの」を集めただけじゃないですか!

そのボケを理解してしまうミーちゃんがヤバいw
しかもツッコミ厳しすぎww

しゅん…😢
②連立方程式を使う解き方
連立方程式で一次関数の式を求めるために必要な材料、方法は以下の通りです。
| 必要な材料 | 2つの点の座標 |
| 方法 | \(y=ax+b\)の\(x\)と\(y\)に座標を入れて 2つの式を作り、連立方程式で解く。 |
一次関数の式を求める計算は、2点の座標さえ分かればこの方法ですべて解けます。
例題4 2点(2,-1)(5,-4)を通る直線の式を求めなさい。
先程のこの問題は、連立方程式でも解けますのでやってみましょう。
\(y=ax+b\)
(2,-1)を代入
\(-1=2a+b\)⇒反対にして⇒\(2a+b=-1\)…①
(5,-4)を代入
\(-4=5a+b\)⇒反対にして⇒\(5a+b=-4\)…②

反対にした方が計算しやすいでおじゃる。
反対にして式を入れ替えて計算するのがオススメじゃ。
①②を連立方程式で解きます。
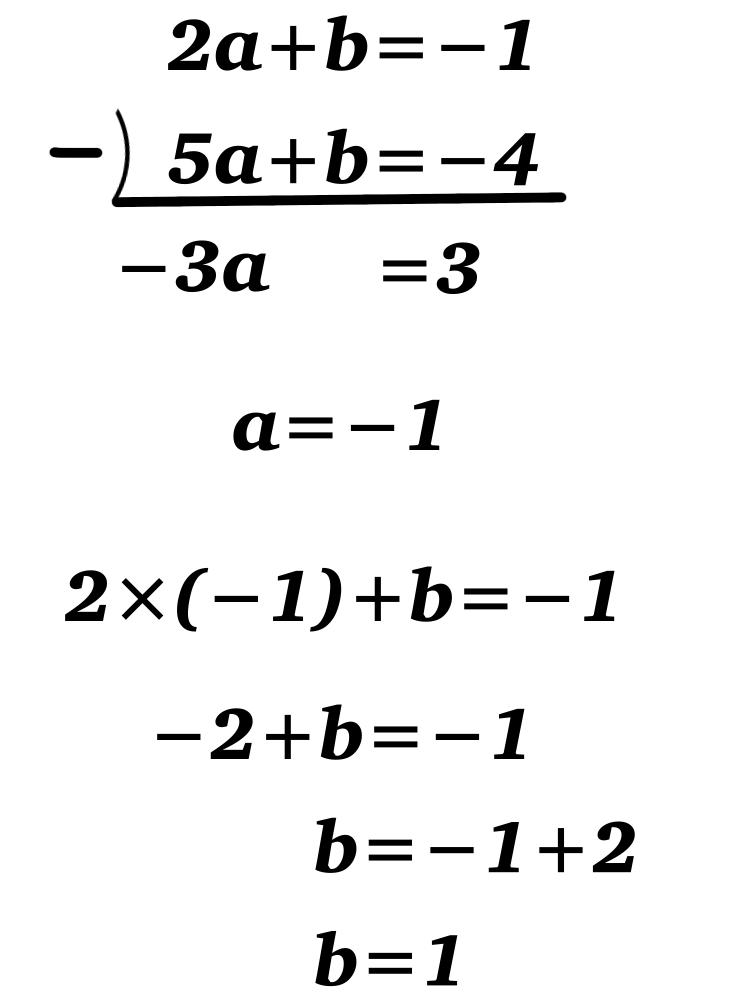
よって、\(y=-x+1\)
この方法は、\(x\)と\(y\)を入れて解けばいいので、考え方としては一番楽かもしれません。でも、連立方程式を解くことになるので計算はちょっと大変です。
2つの点が分かる場合はどちらの方法も使えますが、
傾きを計算してから解く方法⇒傾きを考えるのにちょっと工夫するけど計算は楽
連立方程式を使う方法⇒\(y=ax+b\)に代入するだけで考え方は簡単だけど、計算がちょっと大変
どちらも一長一短。あなたはどっちを使いますか?


一長一短=長所と短所を合わせ持つこと
本当に長くなったりするわけじゃないからね!

でもすごい特技ですね~
さて、私がよく使っている方法を「番外編」として紹介します。
以下の解き方ができるとほぼ計算することなく一次関数の式を出すことができます。
ちなみに私はこの方法を使って暗算で式を出しています。
ハマれば劇的に素早く解ける方法なので紹介しますね。
番外編 グラフを描いて解く方法
今までの例題でやってみましょう。「グラフを描いて解く方法」としましたが、慣れれば頭の中でも解けます!
例題1 傾きが3で、点(-1,4)を通る直線の式を求めなさい。
点(-1,4)を座標にとります。
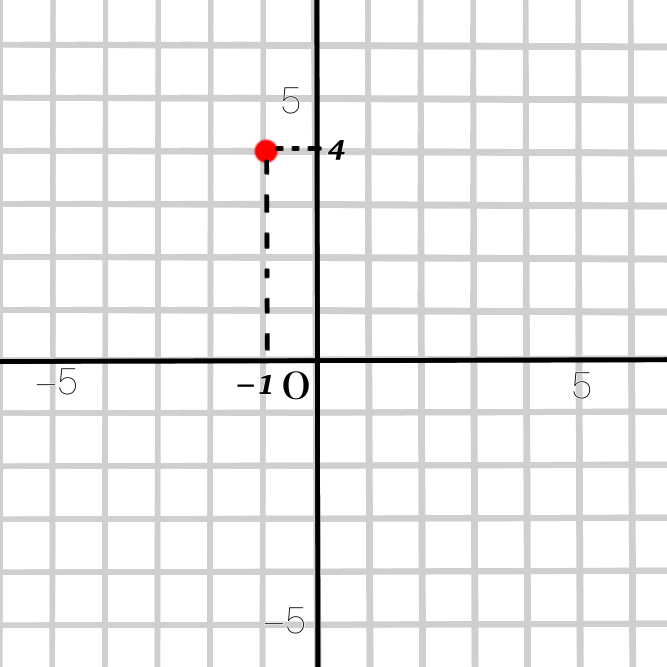
そして傾き3なので、この点から、
「\(x\)が1つ増えたら、\(y\)が3つ増える」の法則で点をとります。
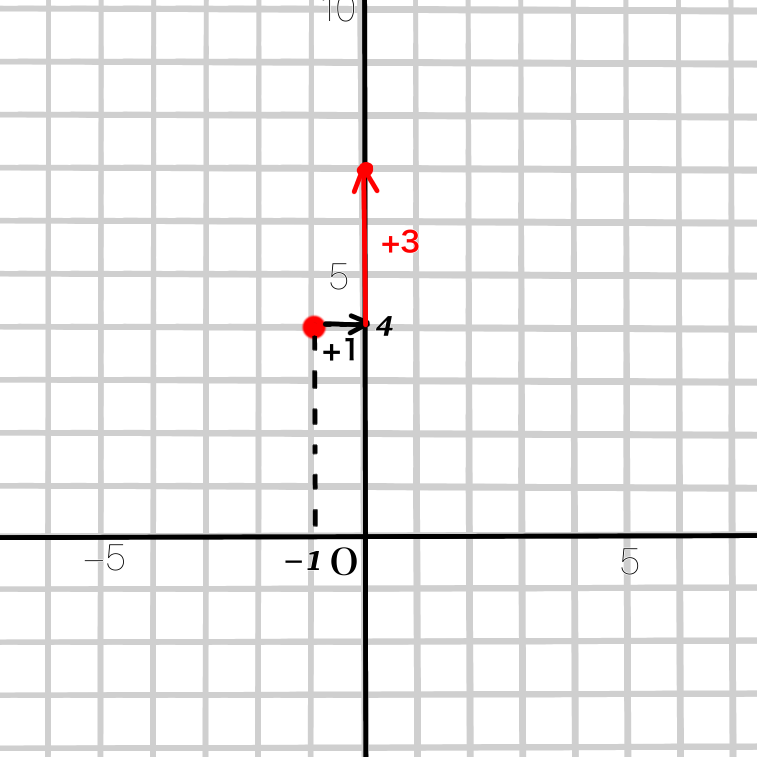
…あら?
\(y\)軸との交点=切片\(b\)なので、
切片がが分かっちゃいましたね。
切片は7です。
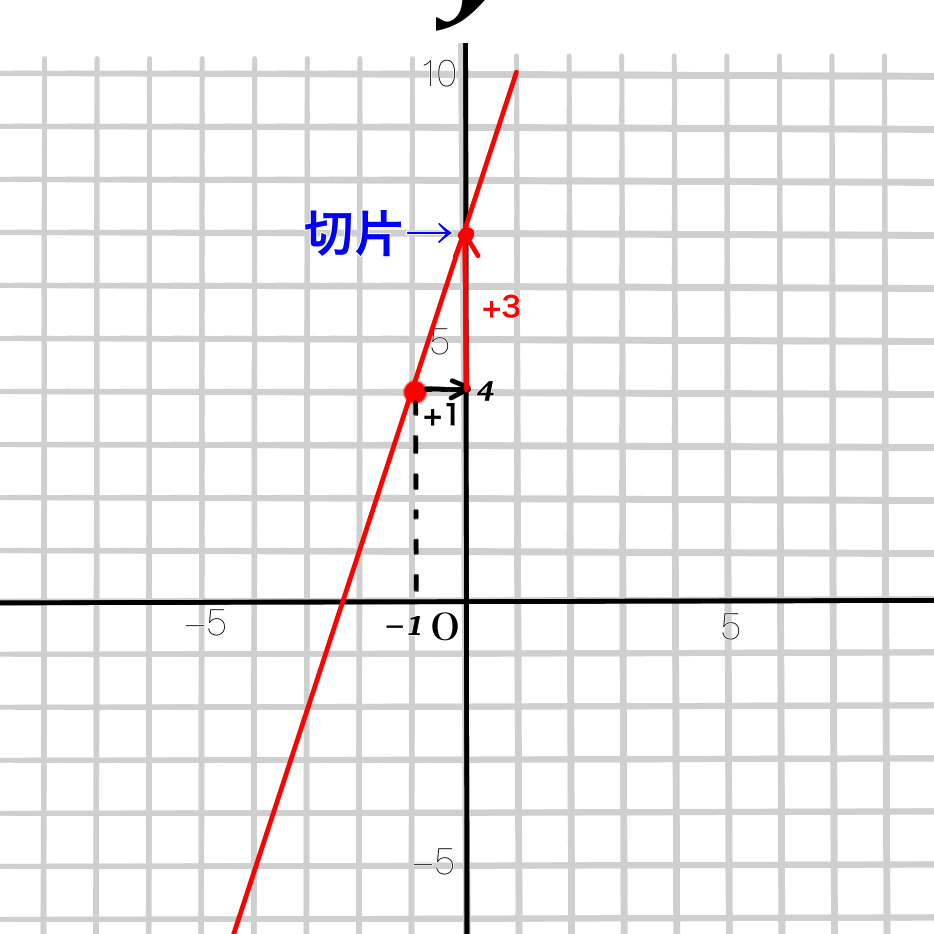
傾きが3、切片が7と分かりました。
答えは\(y=3x+7\)
例題2 切片が-2で、点(-3,10)を通る直線の式を求めなさい。
切片-2を座標にとります。
点(-3,10)を通るので、そこにも点を打ちます。
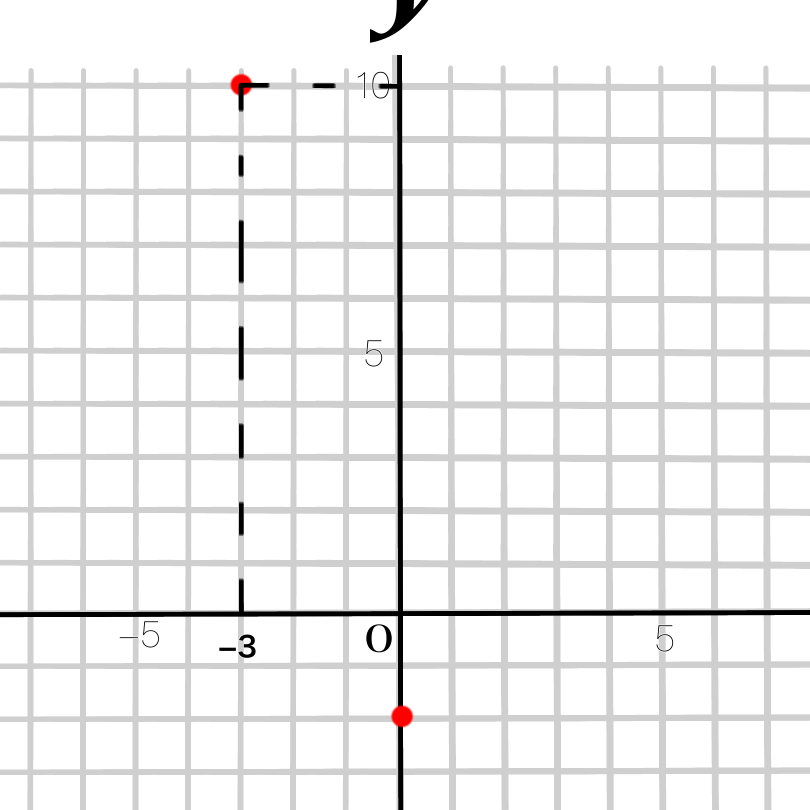
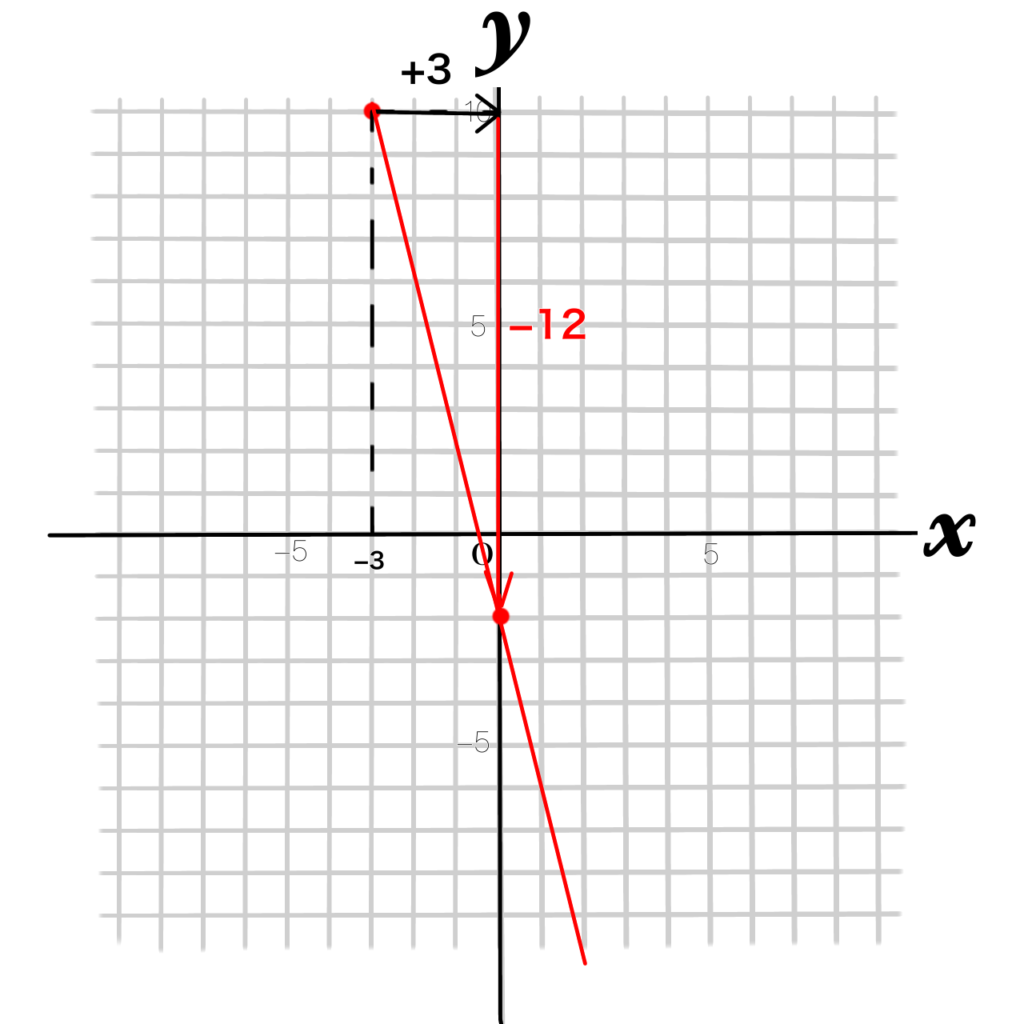
2つの点の間を見てみると、
\(x\)が3つ増えたとき
\(y\)は12個減っていることが分かります。
傾き=\(\dfrac{yの増加量}{xの増加量}\)=\(\dfrac{-12}{3}=-4\)
傾きが-4、切片が-2なので
答えは\(y=-4x-2\)
例題3 \(y=2x+3\)に平行で、点(-4,-2)を通る直線の式を求めなさい
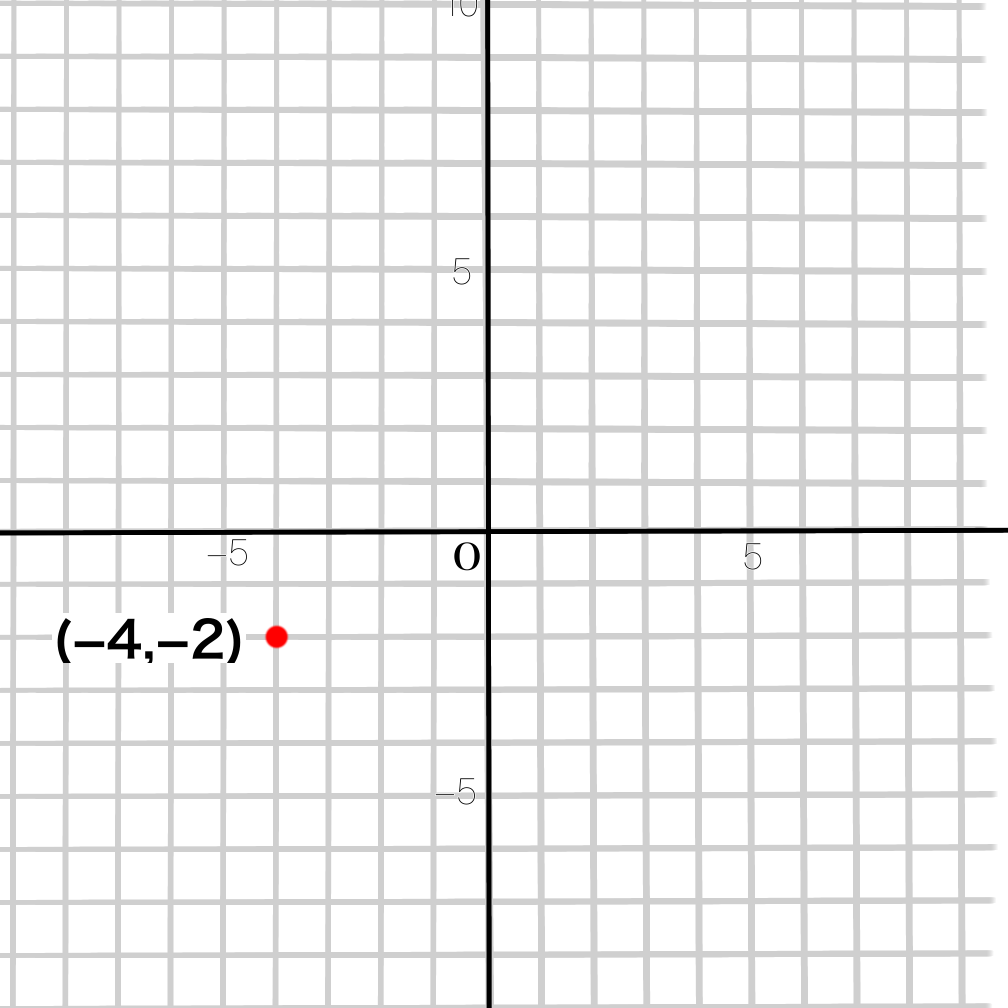
(-4,-2)を座標にとります。
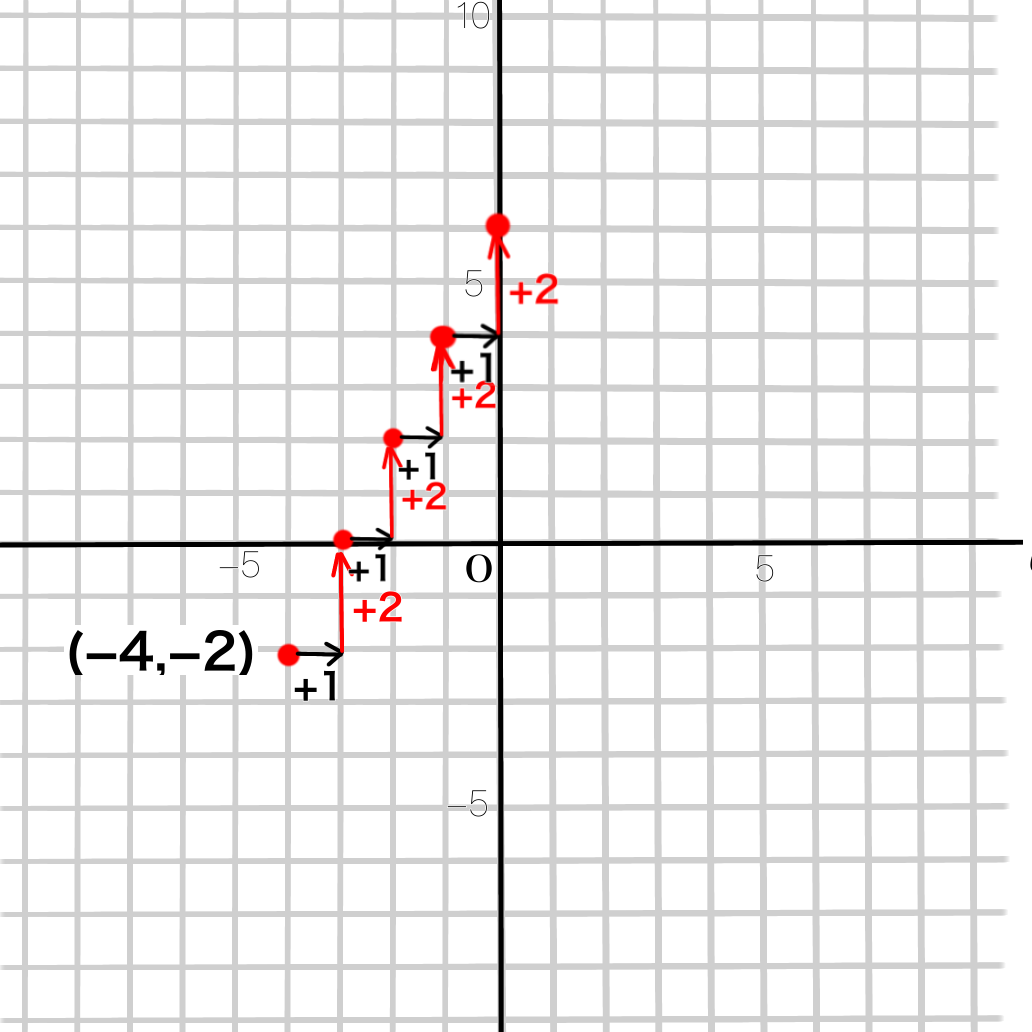
\(y=2x+3\)に平行ということは、傾きが2ということなので(-4,-2)から、
「\(x\)が1つ増えたら、\(y\)が2つ増える」の法則で点を打って、直線を引きます。
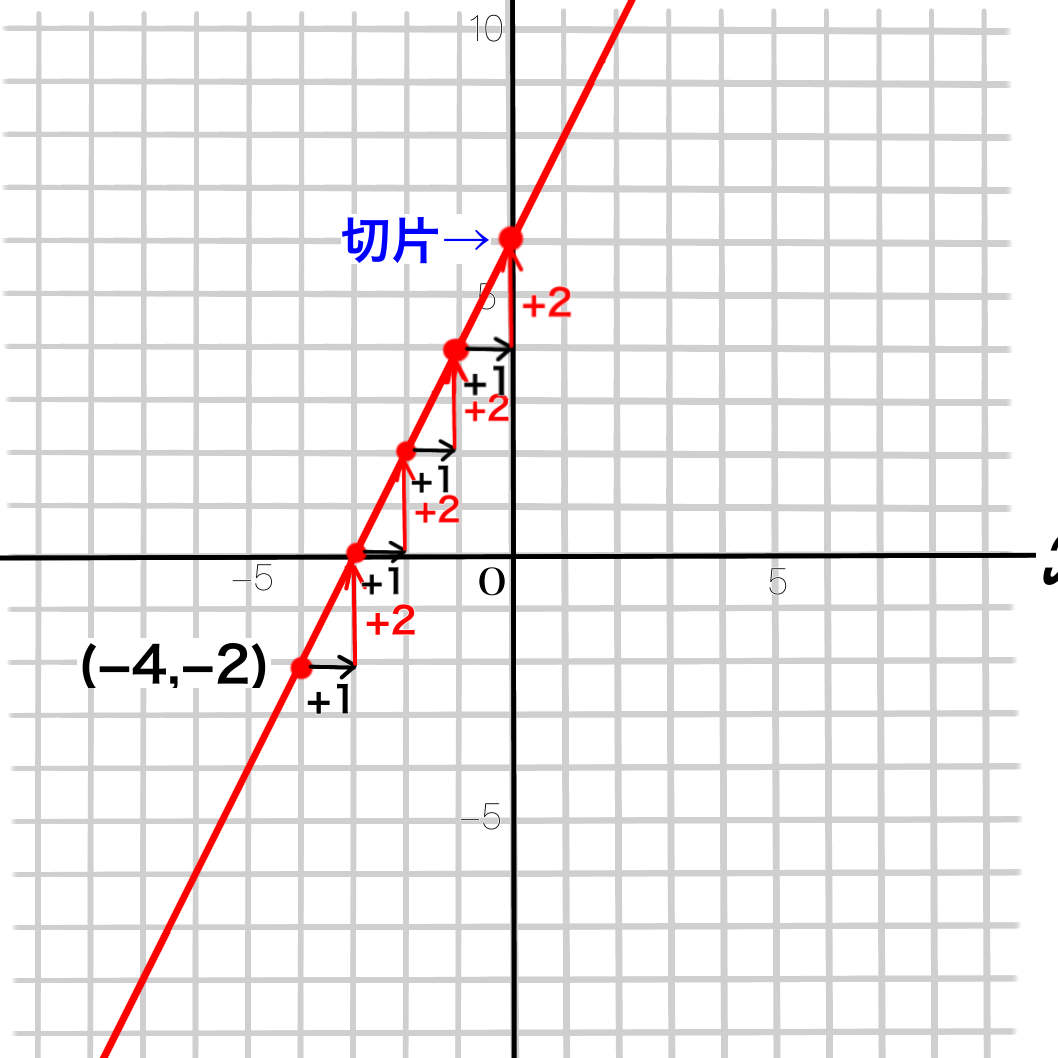
\(y\)軸と交わる点が切片なので、切片は6と分かります。
傾きが2、切片が6なので
答えは\(y=2x+6\)
例題4 2点(2,-1)(5,-4)を通る直線の式を求めなさい。
2点(2,-1)(5,-4)の座標をとって、2点をつなぐ直線を書きます。
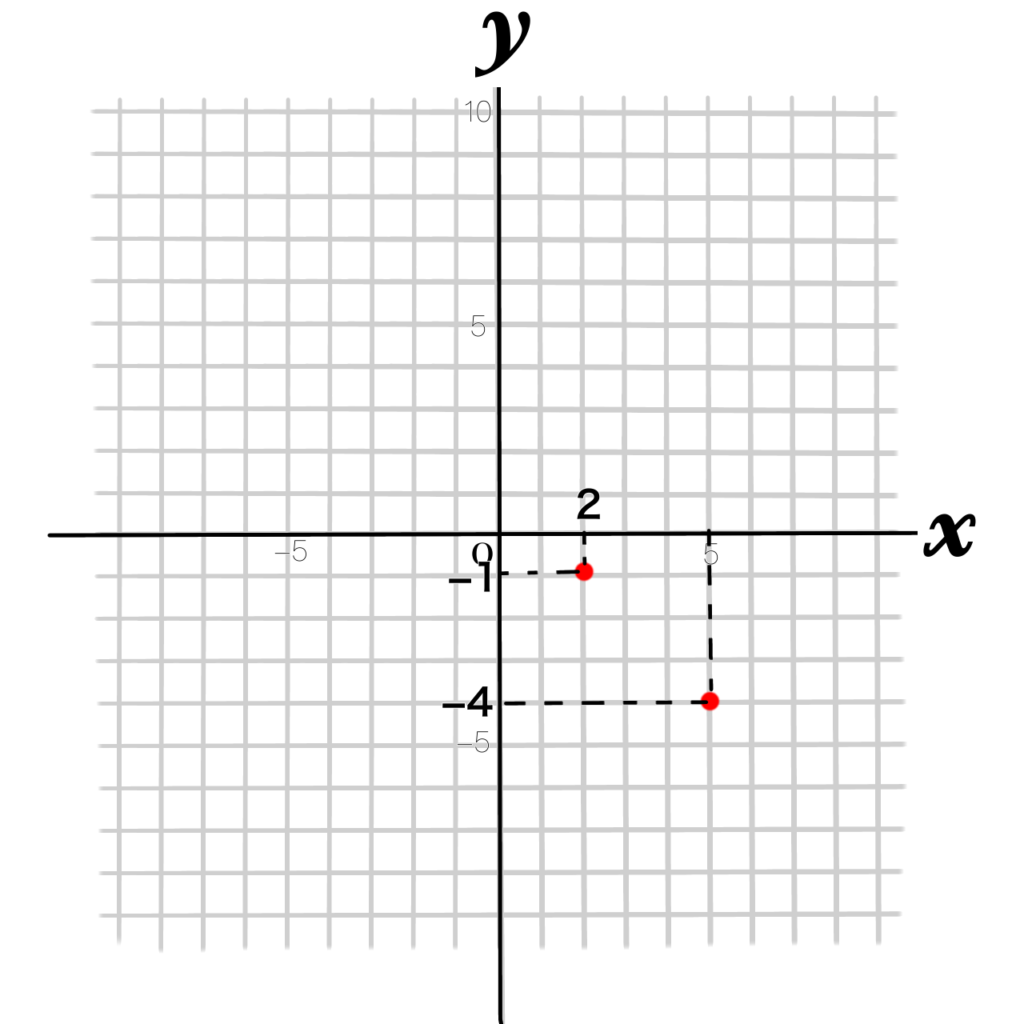
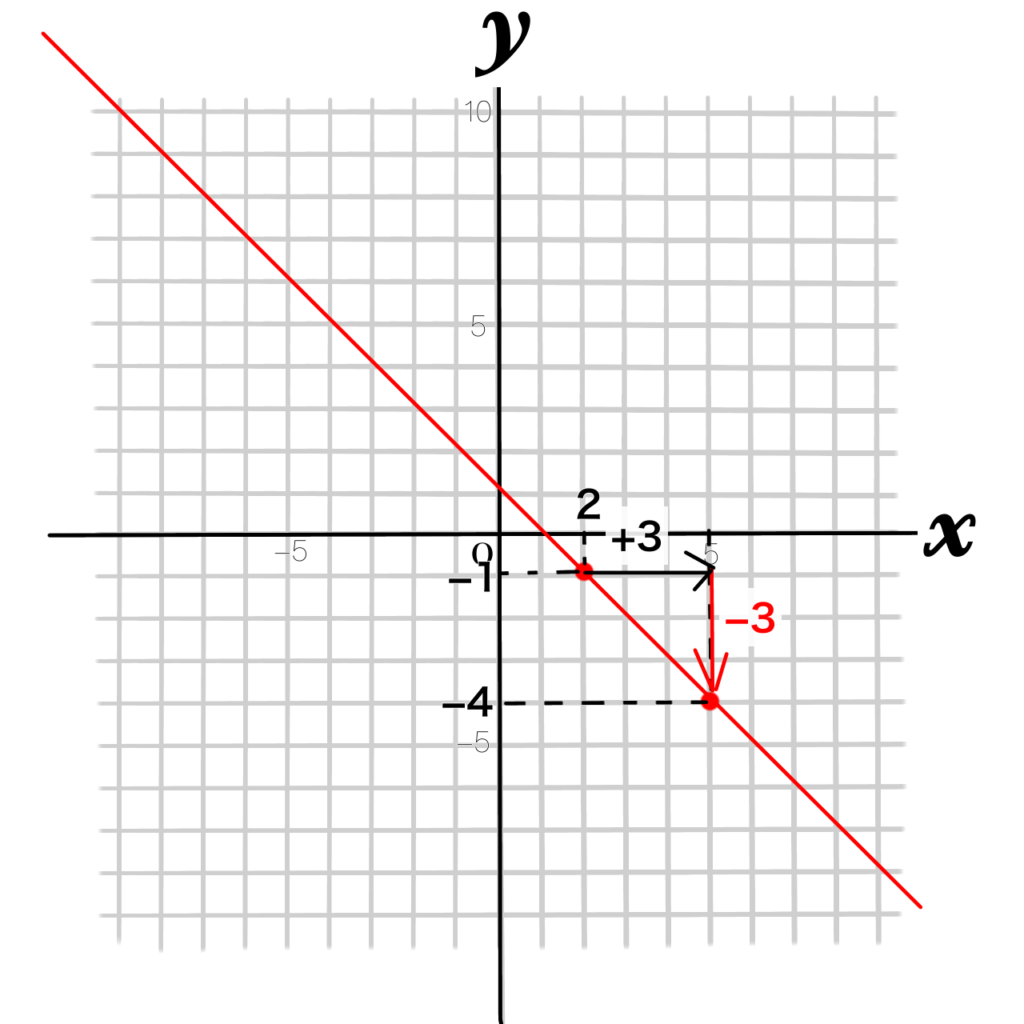
2つの点の間を見ると、\(x\)が3つ増えたとき、\(y\)は3つ減っていることが分かります。
傾き=\(\dfrac{yがいくつ増えたか}{xがいくつ増えたか}\)=\(\dfrac{-3}{3}=-1\)
傾きは-1と分かりました。
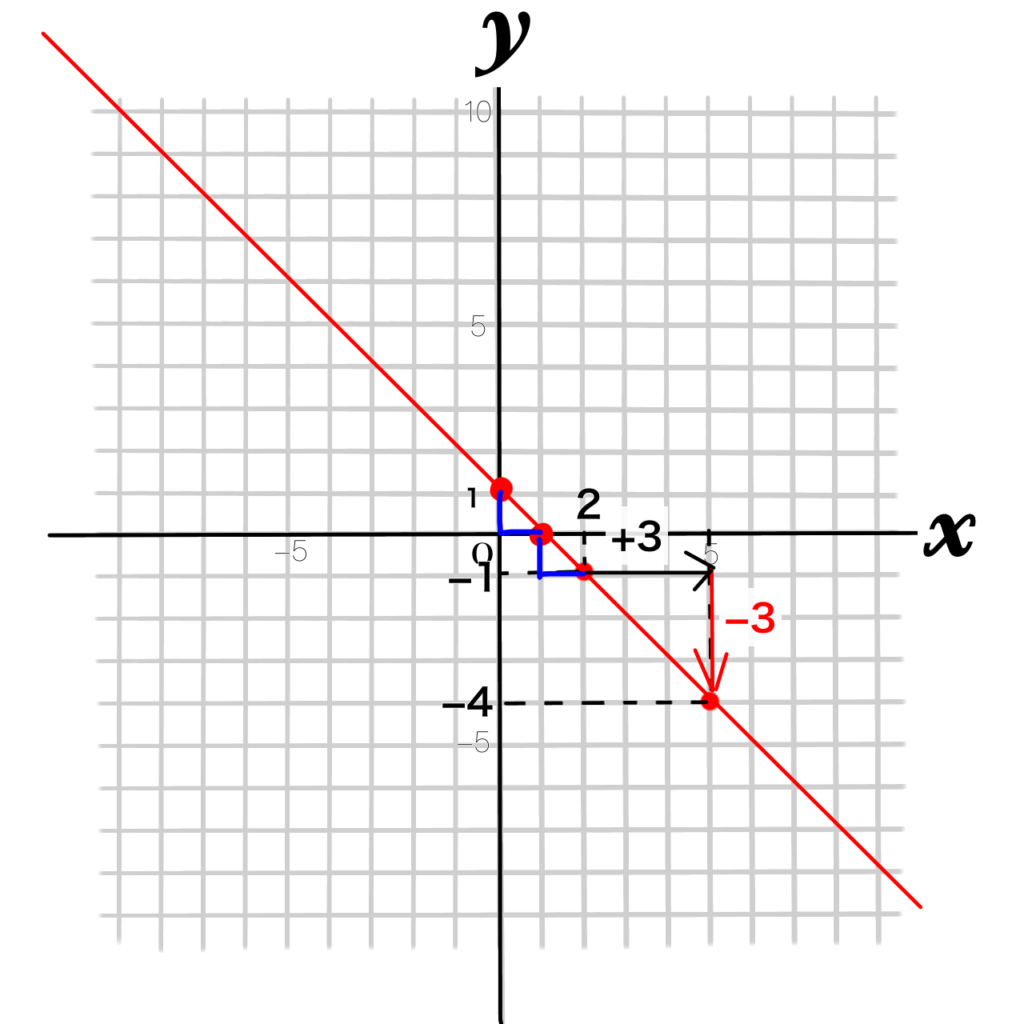
グラフの\(y\)軸上を見ると、もう切片は分かりました。
切片は1です。
傾きが-1、切片が1なので、
答えは\(y=-x+1\)
直線を描かなくても、傾きが-1なので、\(x\)が1つ減ると、\(y\)が1つ増えることになります。
座標が確実に分かる点から、\(y\)軸までたどっていっても切片は分かりますよ!

この方法は、ほぼ計算なしで解けます。応用問題などでもかなり有効ですが、欠点があります。
欠点⇒切片が分数になる式だと面倒
これも実際やってみましょう。
例題5 2点(1,3)(-3,6)を通る直線の式を求めなさい。
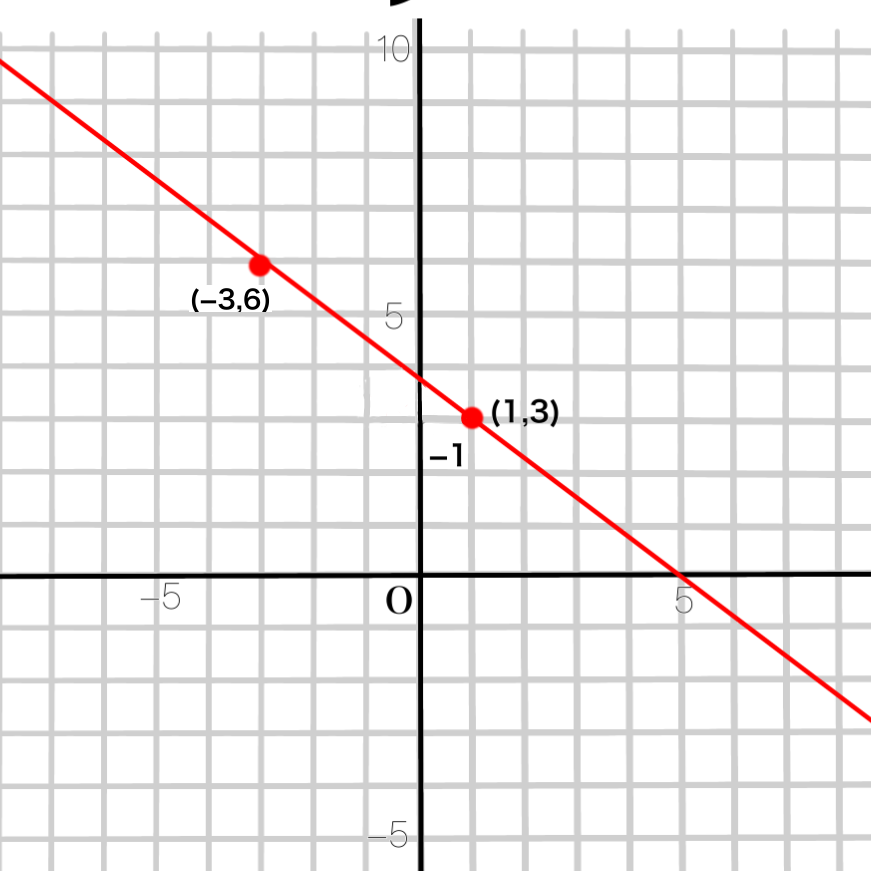
2点とって、直線でつないでみると、\(y\)軸上を通るときにピッタリ整数のところを通っていません。
これだと切片が読み取れません。
じゃあ、こういう場合はどうすればいいのでしょう?
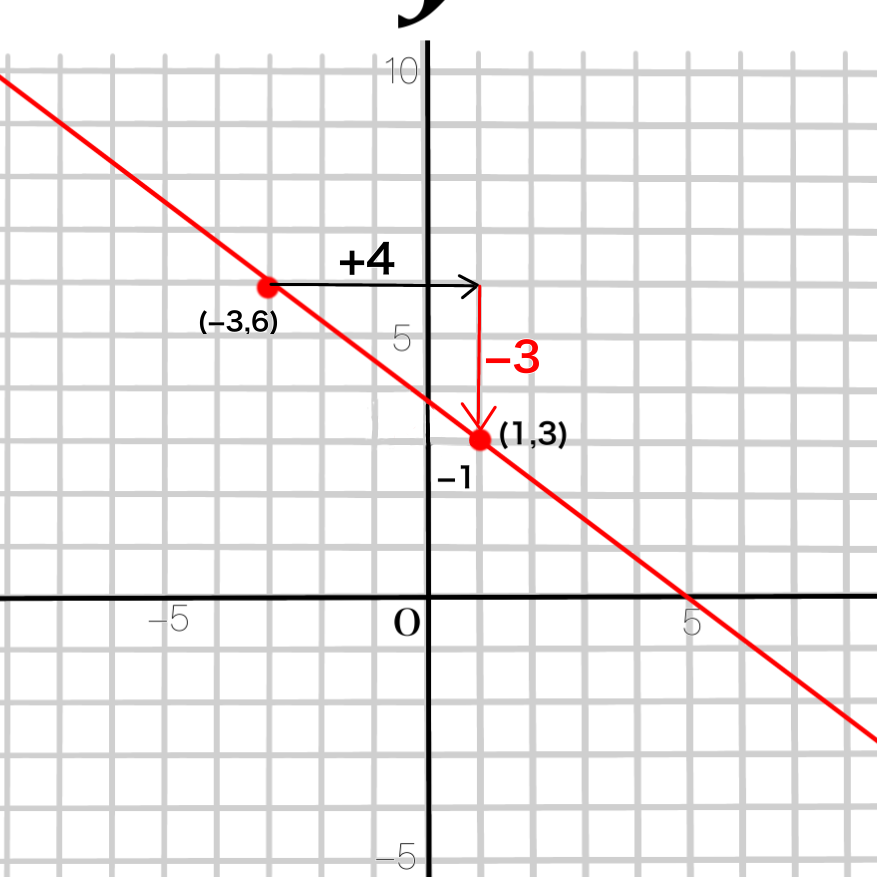
まずは傾きを求めます。
傾き=\(\dfrac{yの増加量}{xの増加量}\)=\(\dfrac{-3}{4}=-\dfrac{3}{4}\)
傾きは、\(x\)が1つ増えたときに\(y\)がいくつ増えるか、減るかを表した数です。
傾き\(-\dfrac{3}{4}\)ですから、\(x\)が1つ増えたときに\(y\)は\(\dfrac{3}{4}\)減ります。
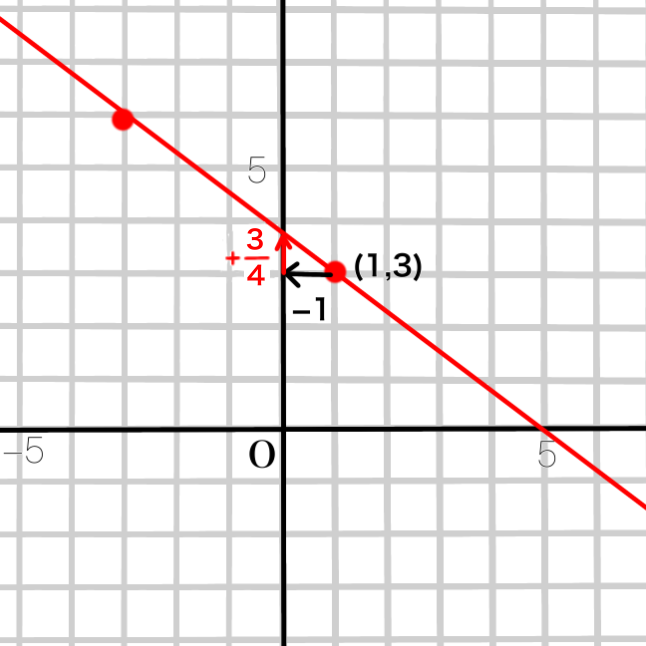
逆に\(x\)が1つ減れば、\(y\)は\(\dfrac{3}{4}\)増えます。
そうすると、点(1,3)から、\(x\)を1つ減らすと、\(y\)は\(\dfrac{3}{4}\)増えるので、
\(3+\dfrac{3}{4}\)=\(\dfrac{15}{4}\)
切片は\(\dfrac{15}{4}\)となります。
よって、答えは
\(y=-\dfrac{3}{4}x+\dfrac{15}{4}\)
…とこんな感じで解けるには解けますが、やっぱりちょっと面倒かもしれません。
この場合にはやはり、教科書に載っている2つの方法のどちらかで計算した方がいいかもしれませんね(それでも面倒でしょうけど)。
でも、切片が整数になる場合はメッチャ速く解けますので、やってみて下さい。
ちょっと慣れは必要ですけど。
最後に
一次関数の式を計算で出す方法とグラフで出す方法を説明をしました。
前に投稿した2つの記事と合わせて読んでもらうと理解が深まると思いますので、読んでください。
この次の記事では、一次関数の利用編を書きたいと思います!
実力テストや模擬試験、入試にもよく出題されるものを解説していきたいと思います!



コメント